目录
404.左叶子之和
513.找树左下角的值
112.路径总和
106.从中序与后序遍历构造二叉树
105.从前序与中序遍历序列构造二叉树
654.最大二叉树
404.左叶子之和
404. 左叶子之和
简单
给定二叉树的根节点 root ,返回所有左叶子之和。
示例 1:
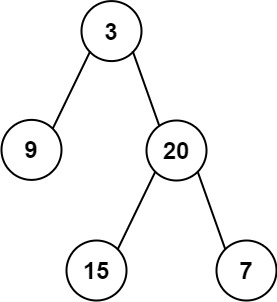
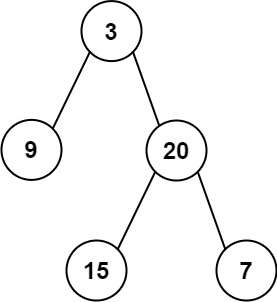
输入: root = [3,9,20,null,null,15,7] 输出: 24 解释: 在这个二叉树中,有两个左叶子,分别是 9 和 15,所以返回 24
示例 2:
输入: root = [1] 输出: 0
提示:
- 节点数在
[1, 1000]范围内 -1000 <= Node.val <= 1000
递归法
定义一个前驱指针指向要处理的节点的父节点,此时可判断该节点是否是左子节点
/*** Definition for a binary tree node.* 二叉树节点的定义* public class TreeNode {* int val; // 节点值* TreeNode left; // 左子节点* TreeNode right; // 右子节点* TreeNode() {} // 默认构造函数* TreeNode(int val) { this.val = val; } // 带值的构造函数* TreeNode(int val, TreeNode left, TreeNode right) { // 带值和子节点的构造函数* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {// 计算左叶子节点的和public int sumOfLeftLeaves(TreeNode root) {// 初始调用 leftLeavesSum 方法,传入 null 作为前一个节点int sum = leftLeavesSum(null, root); return sum; // 返回左叶子节点的和}// 递归计算左叶子节点的和public int leftLeavesSum(TreeNode pre, TreeNode root) {if(root == null){ // 如果当前节点为空,返回 0return 0;}int middleSum = 0; // 用于累加左叶子节点的和// 如果当前节点是左叶子节点且前一个节点不为空且是当前节点的父节点if(root.left == null && root.right == null && pre != null && pre.left == root){middleSum += root.val; // 将当前节点值加入到左叶子节点的和中return middleSum; // 返回当前节点值作为左叶子节点的和}// 递归计算左子树的左叶子节点的和int leftSum = leftLeavesSum(root, root.left);// 递归计算右子树的左叶子节点的和int rightSum = leftLeavesSum(root, root.right);// 返回左叶子节点的和,包括左子树、右子树和当前节点的和return middleSum + leftSum + rightSum;}
}
迭代法
// 层序遍历迭代法
class Solution {public int sumOfLeftLeaves(TreeNode root) {int sum = 0; // 初始化左叶子节点的和if (root == null) return 0; // 如果根节点为空,返回0Queue<TreeNode> queue = new LinkedList<>(); // 创建一个队列用于层序遍历queue.offer(root); // 将根节点加入队列while (!queue.isEmpty()) { // 当队列不为空时,继续遍历int size = queue.size(); // 获取当前层的节点数while (size-- > 0) { // 遍历当前层的所有节点TreeNode node = queue.poll(); // 从队列中取出一个节点if (node.left != null) { // 如果左节点不为空queue.offer(node.left); // 将左节点加入队列if (node.left.left == null && node.left.right == null){ // 判断左节点是否为叶子节点sum += node.left.val; // 如果是左叶子节点,则将其值加入到和中}}if (node.right != null) queue.offer(node.right); // 将右节点加入队列}}return sum; // 返回左叶子节点的和}
}
513.找树左下角的值
513. 找树左下角的值
中等
给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。
假设二叉树中至少有一个节点。
示例 1:
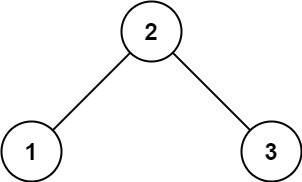
输入: root = [2,1,3] 输出: 1
示例 2:
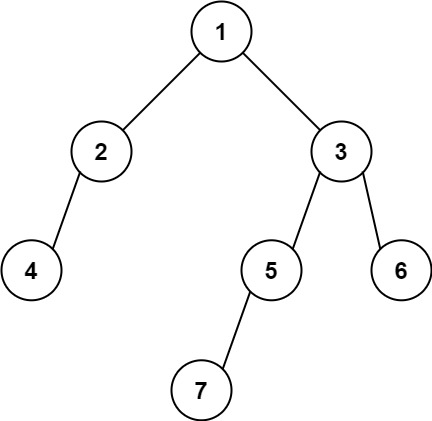
输入: [1,2,3,4,null,5,6,null,null,7] 输出: 7
提示:
- 二叉树的节点个数的范围是
[1,104] -231 <= Node.val <= 231 - 1
递归法:
同一深度的情况下,由于左子树先于右子树遍历,故左侧节点先被更新到value中,而同一层其他节点不会被更新
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/// 解题思路:
// 使用深度优先搜索(DFS)来遍历二叉树,记录最左侧叶子节点的值以及其深度,
// 若当前叶子节点的深度大于已记录的最大深度,则更新最左侧叶子节点的值和深度,
// 最终返回最左侧叶子节点的值。class Solution {int maxDepth = -1; // 初始化最大深度为-1int value = 0; // 初始化最左侧叶子节点的值为0public int findBottomLeftValue(TreeNode root) {leftValue(root, 0); // 调用递归函数return value; // 返回最左侧叶子节点的值}// 递归函数,用于寻找最左侧叶子节点的值public void leftValue(TreeNode root, int depth) {if (root == null) { // 如果当前节点为空,直接返回return;}if (root.left == null && root.right == null && depth > maxDepth) { // 当前节点为叶子节点且深度大于最大深度value = root.val; // 更新最左侧叶子节点的值maxDepth = depth; // 更新最大深度}leftValue(root.left, depth + 1); // 递归遍历左子树,深度加1leftValue(root.right, depth + 1); // 递归遍历右子树,深度加1}
}
迭代法
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution { // findBottomLeftValue方法,接受一个二叉树的根节点作为参数,返回最底层最左边节点的值。 public int findBottomLeftValue(TreeNode root) { // 创建一个队列,用于层序遍历二叉树。 Queue<TreeNode> queue = new LinkedList<>(); // 将根节点加入队列。 queue.offer(root); // 初始化结果变量,用于存储最底层最左边节点的值。 int res = 0; // 当队列不为空时,进行循环。 while (!queue.isEmpty()) { // 获取当前层的节点数量。 int size = queue.size(); // 遍历当前层的所有节点。 for (int i = 0; i < size; i++) { // 取出队列中的一个节点。 TreeNode poll = queue.poll(); // 如果是当前层的第一个节点(即最左边的节点),则更新结果变量的值。 if (i == 0) { res = poll.val; } // 如果该节点有左子节点,则将左子节点加入队列。 if (poll.left != null) { queue.offer(poll.left); } // 如果该节点有右子节点,则将右子节点加入队列。 if (poll.right != null) { queue.offer(poll.right); } } } // 返回结果变量的值,即最底层最左边节点的值。 return res; }
}112.路径总和
112. 路径总和
简单
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
叶子节点 是指没有子节点的节点。
示例 1:
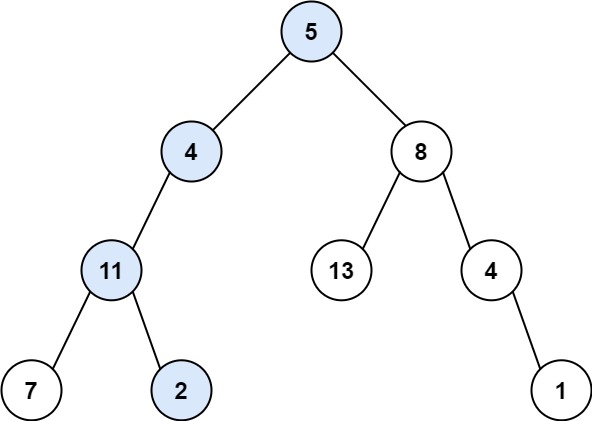
输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22 输出:true 解释:等于目标和的根节点到叶节点路径如上图所示。
示例 2:
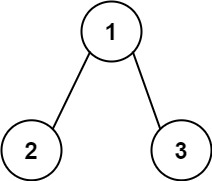
输入:root = [1,2,3], targetSum = 5 输出:false 解释:树中存在两条根节点到叶子节点的路径: (1 --> 2): 和为 3 (1 --> 3): 和为 4 不存在 sum = 5 的根节点到叶子节点的路径。
示例 3:
输入:root = [], targetSum = 0 输出:false 解释:由于树是空的,所以不存在根节点到叶子节点的路径。
提示:
- 树中节点的数目在范围
[0, 5000]内 -1000 <= Node.val <= 1000-1000 <= targetSum <= 1000
递归法:
采用前序遍历,没到一个节点就将targetSum减去该节点的val,如果是根节点的话判断条件并返回,不是根节点的话向左右子树遍历
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
// 定义一个Solution类
class Solution { // hasPathSum方法,接受一个二叉树的根节点root和一个目标值targetSum作为参数 // 返回值为boolean类型,表示是否存在从根节点到叶子节点的路径,使得路径上所有节点的值之和等于targetSum public boolean hasPathSum(TreeNode root, int targetSum) { // 如果根节点为空(即二叉树为空树),则不存在任何路径,返回false if(root == null){ return false; } // 从目标值中减去当前节点的值,更新目标值 targetSum -= root.val; // 如果当前节点是叶子节点(即没有左子节点和右子节点) if(root.left == null && root.right == null){ // 如果更新后的目标值为0,说明从根节点到当前叶子节点的路径上所有节点的值之和正好等于targetSum if(targetSum == 0){ return true; }else{ // 如果不等于0,则说明不存在符合条件的路径,返回false return false; } } // 如果当前节点不是叶子节点,则递归地对左子树和右子树调用hasPathSum方法 // leftResult表示左子树中是否存在符合条件的路径 boolean leftResult = hasPathSum(root.left,targetSum); // rightResult表示右子树中是否存在符合条件的路径 boolean rightResult = hasPathSum(root.right,targetSum); // 如果左子树或右子树中存在符合条件的路径,则返回true;否则返回false return leftResult || rightResult; }
}迭代法:
// 定义一个Solution类
class Solution { // hasPathSum方法,接受一个二叉树的根节点root和一个目标值targetSum作为参数 // 返回值为boolean类型,表示是否存在从根节点到叶子节点的路径,使得路径上所有节点的值之和等于targetSum public boolean hasPathSum(TreeNode root, int targetSum) { // 如果根节点为空(即二叉树为空树),则不存在任何路径,返回false if(root == null){ return false; } // 创建两个队列,一个用于存储节点,另一个用于存储从根节点到当前节点的路径和 Queue<TreeNode> treeNode = new LinkedList<>(); Queue<Integer> count = new LinkedList<>(); // 将根节点和初始的路径和(即目标值)加入队列 treeNode.offer(root); count.offer(targetSum); // 使用while循环进行层序遍历,直到节点队列或路径和队列为空 while(!treeNode.isEmpty() && !count.isEmpty()){ // 取出队列中的节点和对应的路径和 TreeNode node = treeNode.poll(); int countRes = count.poll() - node.val; // 更新路径和,减去当前节点的值 // 如果当前节点是叶子节点(即没有左子节点和右子节点),并且路径和等于0 // 则说明找到了一个从根节点到叶子节点的路径,其路径上所有节点的值之和等于targetSum if(node.left == null && node.right == null && countRes == 0){ return true; } // 如果当前节点有左子节点,则将左子节点和更新后的路径和加入队列 if(node.left != null){ treeNode.offer(node.left); count.offer(countRes); } // 如果当前节点有右子节点,则将右子节点和更新后的路径和加入队列 if(node.right != null){ treeNode.offer(node.right); count.offer(countRes); } } // 如果遍历完所有节点后仍未找到符合条件的路径,则返回false return false; }
}106.从中序与后序遍历构造二叉树
106. 从中序与后序遍历序列构造二叉树
已解答
中等
相关标签
相关企业
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
示例 1:
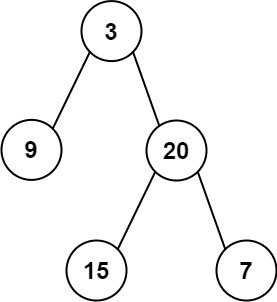
输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3] 输出:[3,9,20,null,null,15,7]
示例 2:
输入:inorder = [-1], postorder = [-1] 输出:[-1]
提示:
1 <= inorder.length <= 3000postorder.length == inorder.length-3000 <= inorder[i], postorder[i] <= 3000inorder和postorder都由 不同 的值组成postorder中每一个值都在inorder中inorder保证是树的中序遍历postorder保证是树的后序遍历
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode buildTree(int[] inorder, int[] postorder) {//因为每次都从postorder中取元素,所以当postorder为空的时候就返回nullif(postorder.length == 0){return null;} //取后序遍历的最后一个节点,即中,作为节点元素int nodeValue = postorder[postorder.length - 1];TreeNode node = new TreeNode(nodeValue);//找到后序数组最后一个元素在中序数组中的位置,即中间节点的位置,作为切割点int middleindex;for(middleindex = 0;middleindex < postorder.length - 1; middleindex ++){if(inorder[middleindex] == nodeValue){break;}}//切割中序数组,找到左子树的中序数组和右子树的中序数组//中间节点之前的,即左子树int[] leftInorder = Arrays.copyOfRange(inorder,0,middleindex);//中间节点之后的,即右子树int[] rightInorder = Arrays.copyOfRange(inorder,middleindex + 1,inorder.length);//切割后序数组,找到左子树的后序数组和右子树的后序数组//删除已经操作过的后序数组的最后一个元素postorder = Arrays.copyOfRange(postorder,0,postorder.length - 1);int[] leftPostorder = Arrays.copyOfRange(postorder,0,middleindex);int[] rightPostorder = Arrays.copyOfRange(postorder,middleindex,postorder.length);// 递归地构建左子树和右子树,并将它们分别设置为当前节点的左孩子和右孩子node.left = buildTree(leftInorder,leftPostorder);node.right = buildTree(rightInorder,rightPostorder);return node;}
}105.从前序与中序遍历序列构造二叉树
105. 从前序与中序遍历序列构造二叉树
中等
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] 输出: [3,9,20,null,null,15,7]
示例 2:
输入: preorder = [-1], inorder = [-1] 输出: [-1]
提示:
1 <= preorder.length <= 3000inorder.length == preorder.length-3000 <= preorder[i], inorder[i] <= 3000preorder和inorder均 无重复 元素inorder均出现在preorderpreorder保证 为二叉树的前序遍历序列inorder保证 为二叉树的中序遍历序列
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode buildTree(int[] preorder, int[] inorder) {//由于每次都是从前序数组中取元素,当前序数组为空时,返回nullif(preorder.length == 0){return null;}//当前序数组不为空时,从中取得第一个元素作为中间节点int nodeValue = preorder[0];TreeNode node = new TreeNode(nodeValue);//找到该中间节点(即第一个元素)在中序数组中的位置int middleIndex;for(middleIndex = 0;middleIndex < inorder.length - 1;middleIndex ++){if(inorder[middleIndex] == nodeValue){break;}}//切割中序数组,分为左子树的中序数组和右子树的中序数组int[] leftInorder = Arrays.copyOfRange(inorder,0,middleIndex);int[] rightInorder = Arrays.copyOfRange(inorder,middleIndex + 1,inorder.length);//切割前序数组,分为左子树的前序数组和右子树的前序数组//先删除数组中已经取出的中间节点preorder = Arrays.copyOfRange(preorder,1,preorder.length);int[] leftPreorder = Arrays.copyOfRange(preorder,0,middleIndex);int[] rightPreorder = Arrays.copyOfRange(preorder,middleIndex,preorder.length);// 递归地构建左子树和右子树,并将它们分别设置为当前节点的左孩子和右孩子node.left = buildTree(leftPreorder,leftInorder);node.right = buildTree(rightPreorder,rightInorder);return node;}
}654.最大二叉树
654. 最大二叉树
中等
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
- 创建一个根节点,其值为
nums中的最大值。 - 递归地在最大值 左边 的 子数组前缀上 构建左子树。
- 递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。
示例 1:
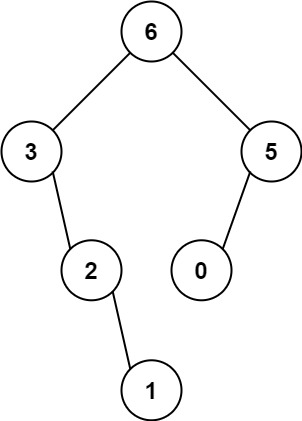
输入:nums = [3,2,1,6,0,5] 输出:[6,3,5,null,2,0,null,null,1] 解释:递归调用如下所示: - [3,2,1,6,0,5] 中的最大值是 6 ,左边部分是 [3,2,1] ,右边部分是 [0,5] 。- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。- 空数组,无子节点。- [2,1] 中的最大值是 2 ,左边部分是 [] ,右边部分是 [1] 。- 空数组,无子节点。- 只有一个元素,所以子节点是一个值为 1 的节点。- [0,5] 中的最大值是 5 ,左边部分是 [0] ,右边部分是 [] 。- 只有一个元素,所以子节点是一个值为 0 的节点。- 空数组,无子节点。
示例 2:
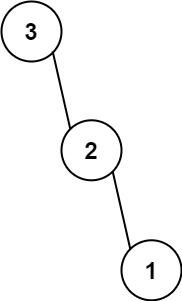
输入:nums = [3,2,1] 输出:[3,null,2,null,1]
提示:
1 <= nums.length <= 10000 <= nums[i] <= 1000nums中的所有整数 互不相同
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution { // 返回构建好的最大二叉树的根节点 public TreeNode constructMaximumBinaryTree(int[] nums) { // 如果数组为空,则返回null,因为不能构建二叉树 if(nums.length == 0){ return null; } // 初始化最大值和最大值的索引为-1和0 int max = -1; int maxIndex = 0; // 遍历数组,找到最大值及其索引 for(int i = 0; i < nums.length; i++){ if(nums[i] > max){ max = nums[i]; maxIndex = i; } } // 创建一个新的树节点,值为数组中的最大值 TreeNode node = new TreeNode(max); // 使用Arrays类的copyOfRange方法,复制最大值左边的部分数组作为左子树的输入数组 int[] leftNums = Arrays.copyOfRange(nums, 0, maxIndex); // 使用Arrays类的copyOfRange方法,复制最大值右边的部分数组作为右子树的输入数组 int[] rightNums = Arrays.copyOfRange(nums, maxIndex + 1, nums.length); // 递归地构建左子树和右子树,并将它们分别设置为当前节点的左孩子和右孩子 node.left = constructMaximumBinaryTree(leftNums); node.right = constructMaximumBinaryTree(rightNums); // 返回构建好的最大二叉树的根节点 return node; }
}
![LeetCode 刷题 [C++] 第45题.跳跃游戏 II](https://img-blog.csdnimg.cn/direct/3f4bcf9e96d44d87a3e46957c5fe269b.png)




![[HackMyVM] 靶场 Wave](https://img-blog.csdnimg.cn/direct/497d860c7f4a472a8a92f1c75f06557b.png)