数的范围刷题笔记-编程知识

数的范围刷题笔记

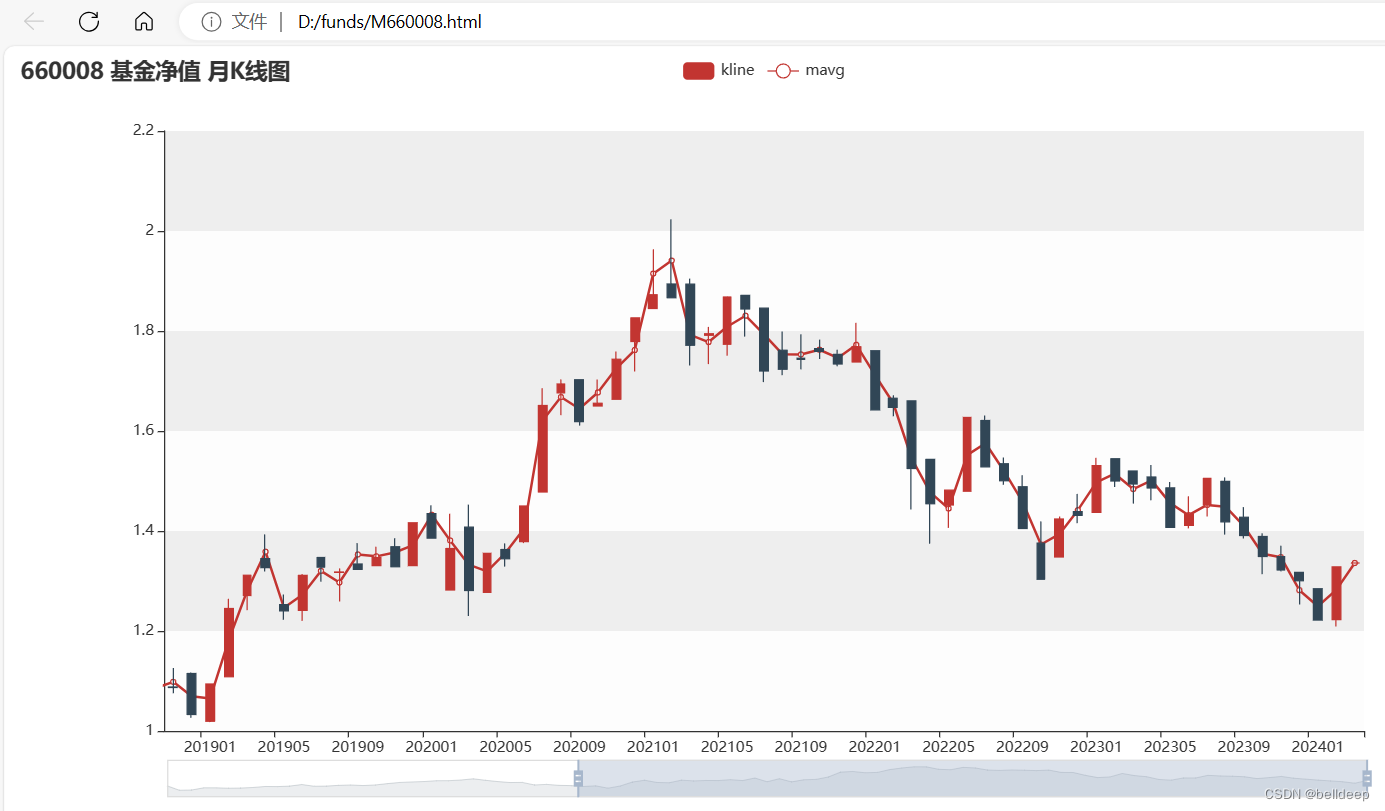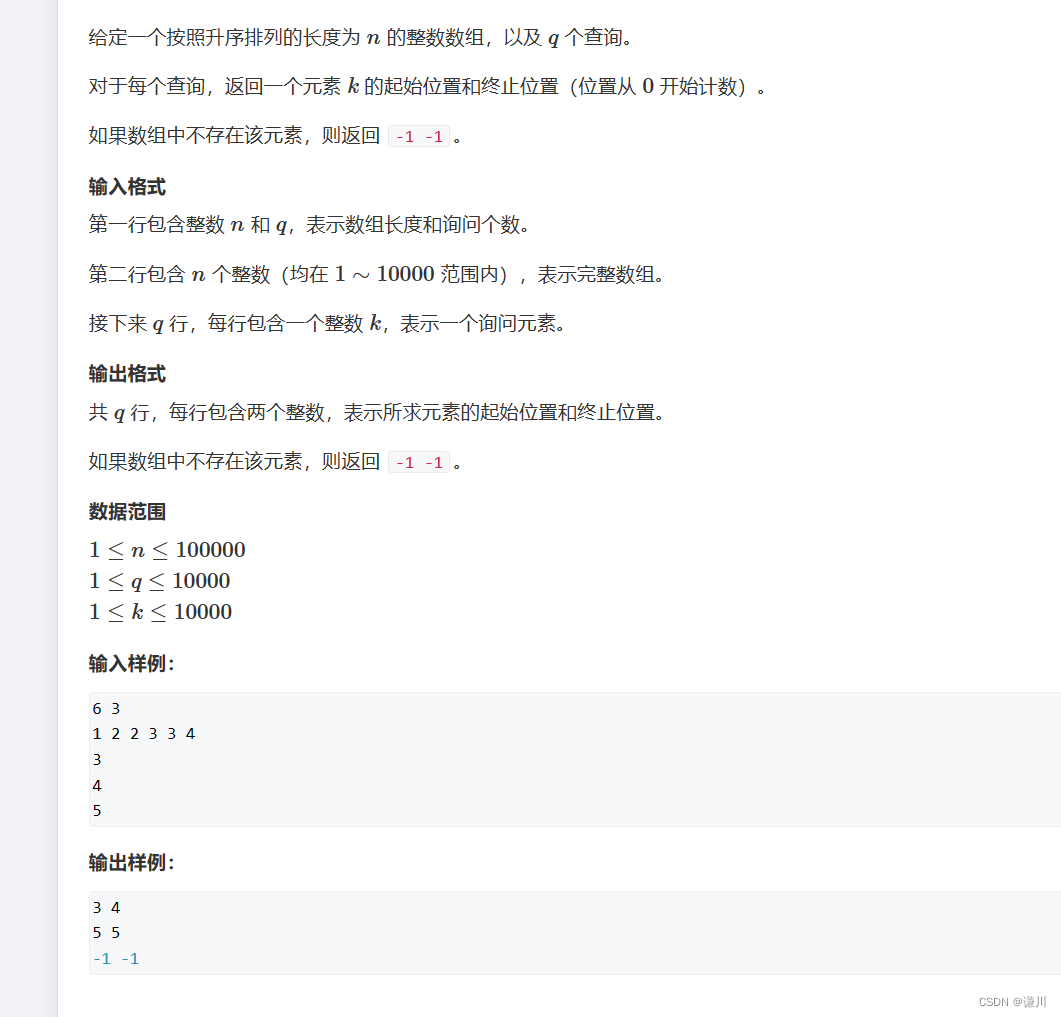
思路寻找第一个大于等于目标的数

因为该数组是升序的所以我们可以采用二分的方式

逼近答案

定义一个左指针和一个右指针

当左右指针重合时

就是我们要找的答案

当我们寻找第一个大于等于x的数时

a[mid]>=x,答案在mid处或者在mid的左边

因此让r=mid继续逼近

如果中间值小于x说明答案在右边

并且必定不在mid 处

因此让l=mid+1；

下面寻找右端点

当a[mid]<=x;

说明答案在mid 处或者在mid 的右边

因此让l=mid;

否则让r=mid-1;

为了避免陷入死循环

我们要讨论特殊情况

例如当l指向3，r指向4，；

且3为左端点 4为右端点

寻找左端点时

mid=(3+4)>>1=3;

此时a[3]=x,让r=mid=3;

完成重合

当寻找右端点时如果还是

mid=(l+r)>>1;

a[mid]=x,让l=mid=3,并未发生改变陷入了死循环

因此我们在找右端点要+1 让mid上取整

mid=（l+r+1）/2=4；

此时让l=mid=4;

完成重合

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,q;
const int N=1e5+10;
int a[N];

int main(){
   cin>>n>>q;
   for(int i=0;i<n;i++){
       cin>>a[i];

   }
   while(q--){
       int x;
       cin>>x;
       int l=0,r=n-1;
       while(l<r){
           int mid=l+r>>1;
           if(a[mid]>=x){
               r=mid;
           }else{
               l=mid+1;
           }
       }
       if(a[r]==x)
       {
           cout<<r<<' ';
           int r=n-1;
           while(l<r){
               int mid=l+r+1>>1;
               if(a[mid]<=x){
                   l=mid;
               }else{
                   r=mid-1;
               }
           }
           cout<<r<<endl;
       }else
       {
           cout<<-1<<' '<<-1<<endl;
       }

   }
   return 0;
}