[P99] 三角形数字的位置

我们都知道著名的杨辉三角，长下面这个样子：

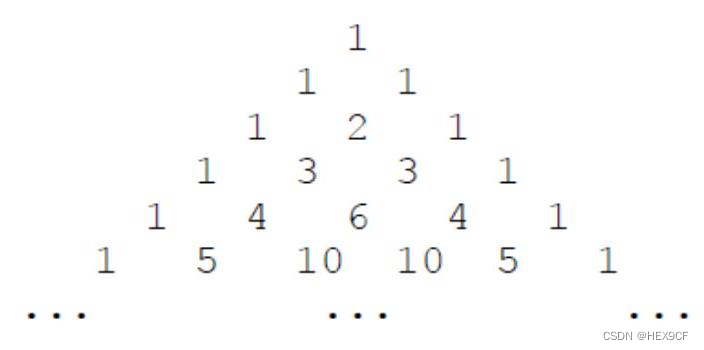
   11 11 2 1
1 3 3 1
...

将他们从上往下可以排列为：1,1,1,1,2,1,1,3,3,1,... 这样一个数列。

有$q$次询问，每次询问请你求出数字$N$第一次在数列中出现的位置。

输入描述

第一行一个整数$q$。$(1\le q\le 10^5)$

对于每次询问，一行一个整数$N$。$(1\le N\le 10^9)$

输出描述

一个整数表示结果。

输入样例

3
3
1
6

输出样例

8
1
13

---

思路

首先，从输入中读取测试用例的数量q，并将每个测试用例的值n存入数组n[]，同时在映射m1中对应的键值设为-1。

对于杨辉三角的每一行，使用动态规划的方法计算组合数，存入二维数组dp[][]。在计算过程中，如果计算得到的组合数大于1e9，则停止计算，因为题目中给出的n的最大值为1e9。如果映射m1中存在这个组合数，并且其对应的值为-1（即还未被赋过值），则将其值设为当前的位置，这里的位置是通过等差数列求和公式计算得出的。

对于映射m1中还未被赋过值的键，使用等差数列求和公式计算其值，这里的值代表的是数字在杨辉三角数列中出现的位置。

最后，对于每个测试用例，输出其在杨辉三角数列中出现的位置，这个位置就是映射m1中对应的值。

注意

1. 在计算位置时，要将乘法结果强制转换为 long long 类型，否则无法通过部分测试点。
2. 动态规划的 j 是从1开始的，会把数字$1$的判断漏掉。数字$1$第一次在数列中出现的位置一定是1，要写 m1[1] = 1;。

---

AC代码

#include <iostream>
#include <map>
#define AUTHOR "HEX9CF"
using namespace std;
using ll = long long;const int N = 1e6 + 7;int q;
ll n[N];
ll dp[2][N];
map<ll, ll> m1;int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> q;for (int i = 1; i <= q; i++) {// 离线处理cin >> n[i];m1[n[i]] = -1;}m1[1] = 1;for (int i = 1; i <= 1e5; i++) {int t = i & 1;dp[t][0] = 1;for (int j = 1; j <= i; j++) {// 求组合数dp[t][j] = dp[t ^ 1][j - 1] + dp[t ^ 1][j];if (dp[t][j] > 1e9) {break;}if (m1.count(dp[t][j]) && !~m1[dp[t][j]]) {// 等差数列求和m1[dp[t][j]] = (1ll * i * (i - 1) / 2) + j + 1;}}}for (auto &i : m1) {if (!~i.second) {// 等差数列求和// 在第f+1行的第二个位置i.second = i.first * (i.first + 1) / 2 + 2;}}// 回答for (int i = 1; i <= q; i++) {cout << m1[n[i]] << "\n";}return 0;
}