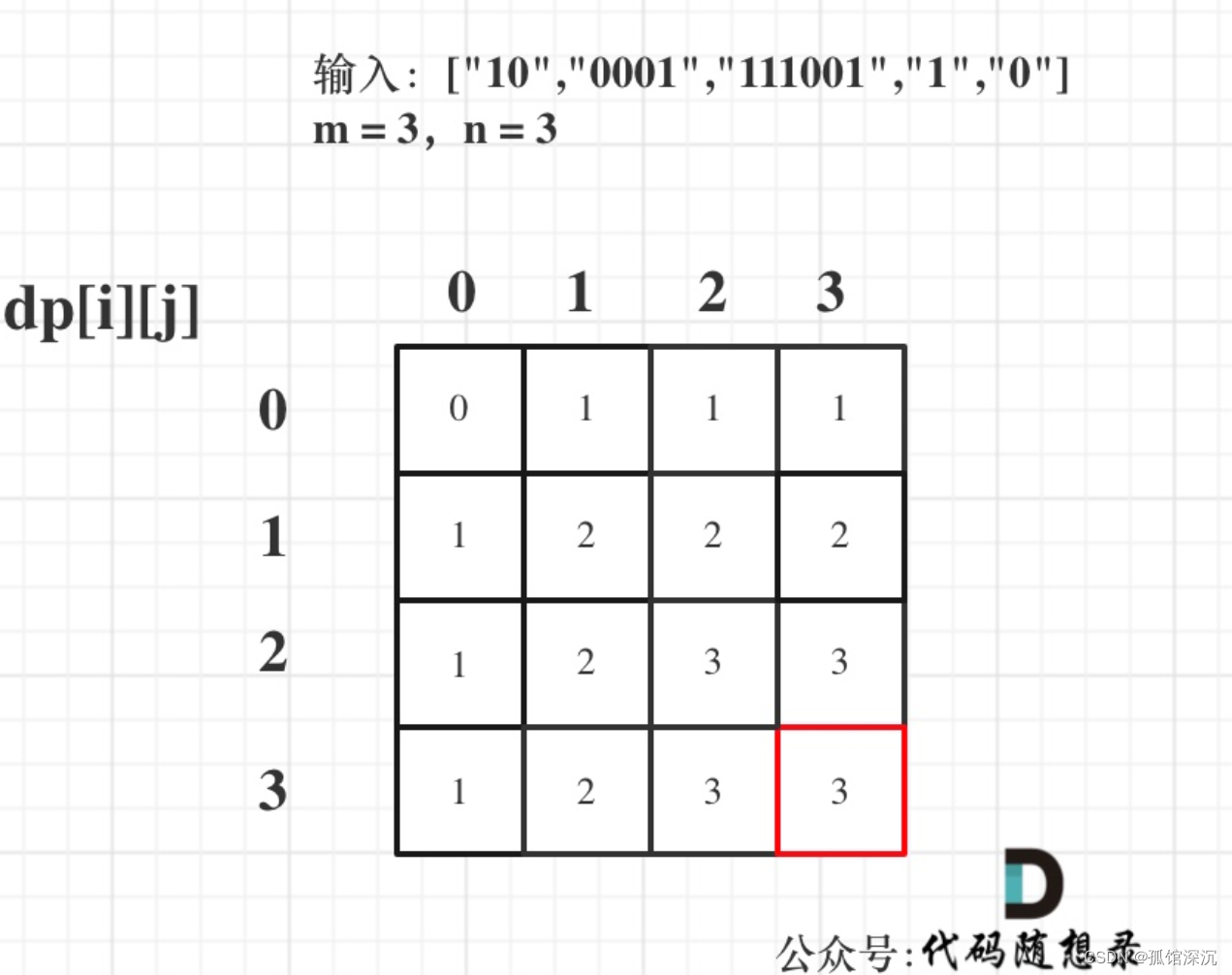
目录
🎈概念
🎈操作-查找
🎈操作-插入
🎈操作-删除(难点)
🎈概念
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
二叉搜索树 左<根<右
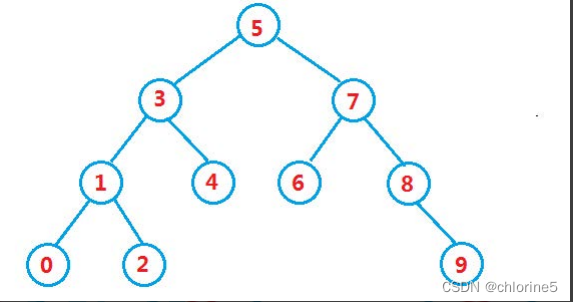
🎈操作-查找
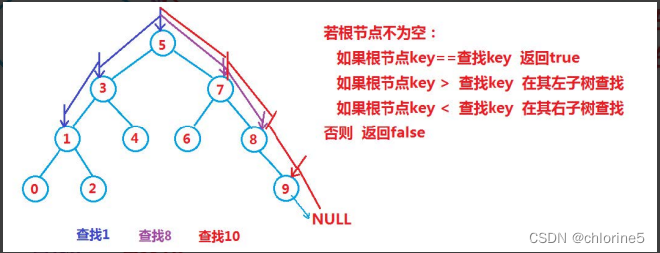
我们根据上述的红色文字进行搜索查找。
public boolean search(int key) {TreeNode cur = root;while (cur != null) {//如果值小于关键字,那么去二叉树的右边if (cur.val < key) {cur = cur.right;//如果值大于关键字,那么去二叉树的左边} else if (cur.val > key) {cur = cur.left;} else {return true;}}return false;}🎈操作-插入
思路:如果这个树是空树,我们就直接插入
如果这个树不是空树,按照查找的逻辑进行插入位置,插入新结点。
- 如果根节点==val 返回false
- 如果根节点< val 去cur左子树查找
- 如果根节点>val 去cur右子树查找
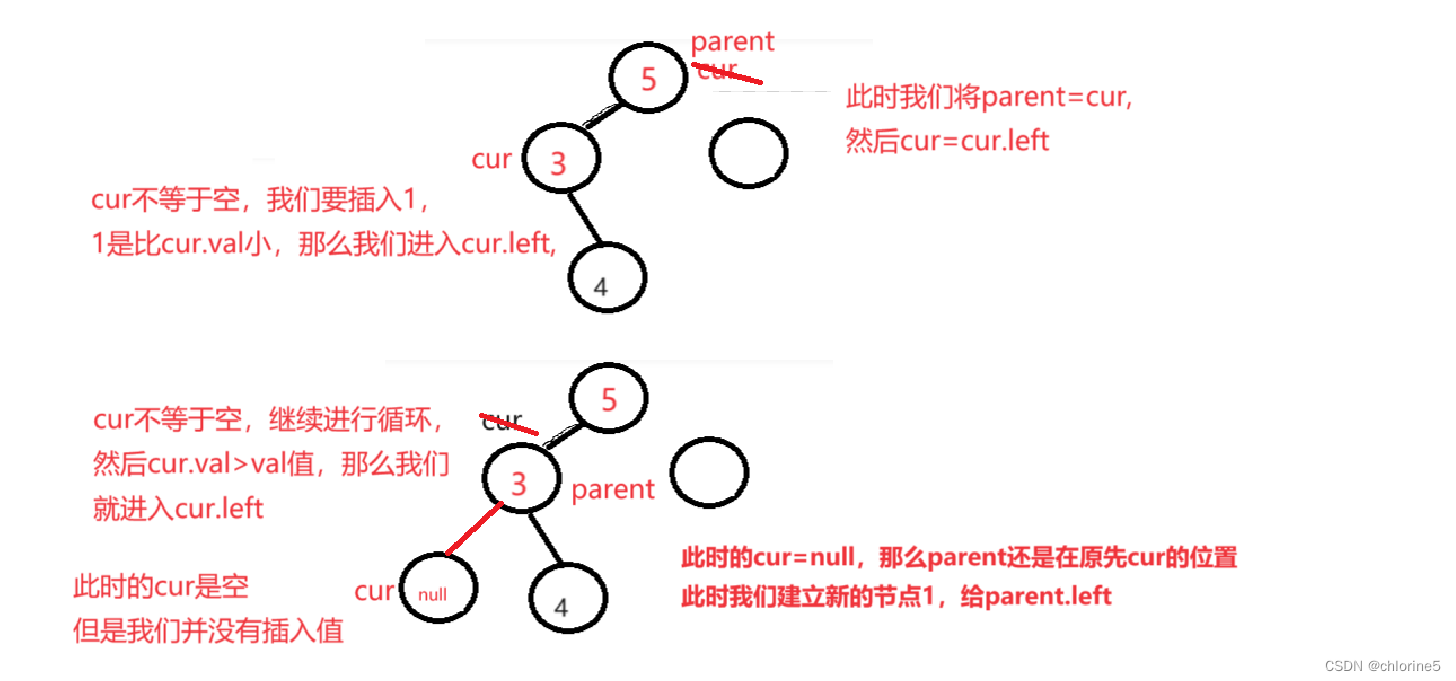
cur==null的时候,我们就要插入该节点(但是我们发现,如果遇到cur==null的时候,cur到了空的地方去,那谁记录cur的父节点呢?怎么给节点给cur所在位置呢?
我来用图给你们展示一下

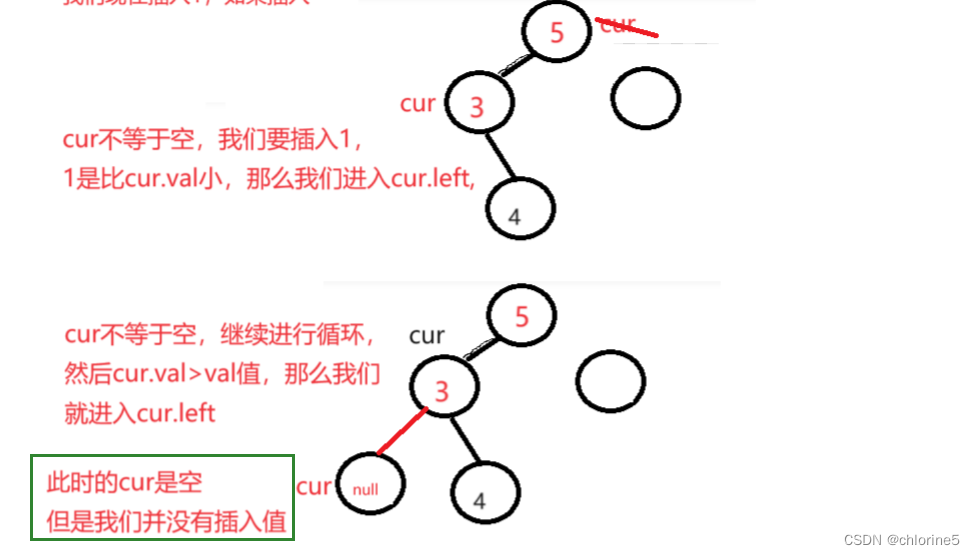
此时我们通过cur=cur.left ,cur到了null的位置,然后我们要进行,插入值,该如何插入呢,此时我们就得给cur的父节点也记录下来,然后让node=parent.left。
/*** 插入** @param val* @return true 表示插入成功, false 表示插入失败*/public boolean insert(int val) {//如果是空树,那么就将val直接给根if (root == null) {root = new TreeNode(val);return true;}TreeNode cur = root;TreeNode parent = null;while (cur != null) {if (val < cur.val) {parent = cur;cur = cur.left;} else if (val > cur.val) {parent = cur;cur = cur.right;} else {return false;}}//上面并没有将新的节点插入进去//我们看到上面不管是cur.right还是cur.left赋值给cur后,cur=null,此时的值并没有插入进行,而是判空结束了TreeNode node = new TreeNode(val);if (parent.val > val) {//插入到左边parent.left = node;} else {parent.right = node;}//我们看到parent的作用其实就是当cur==null的时候//我们需要插入return true;}🎈操作-删除(难点)
设待删除结点为 cur, 待删除结点的双亲结点为 parent
- 1. cur 是 root,则 root = cur.right
- 2. cur 不是 root,cur 是 parent.left,则 parent.left = cur.right
- 3. cur 不是 root,cur 是 parent.right,则 parent.right = cur.right
如果cur的左边空
cur在parent的左边,但是cur的左边空,那么我们将cur的右边节点给parent的左边
cur在parent的右边,但是cur的左边空,那么我们将cur的右边节点给parent的右边
(cur在parent的哪一边,就将cur左右哪一个不为空的节点给parent的哪一边) - 1. cur 是 root,则 root = cur.left
- 2. cur 不是 root,cur 是 parent.left,则 parent.left = cur.left
- 3. cur 不是 root,cur 是 parent.right,则 parent.right = cur.left
cur左边为空,那么就将cur的左边节点 要么给parent的左边,那么parent的右边 //(取决于 cur在parent的哪一边)
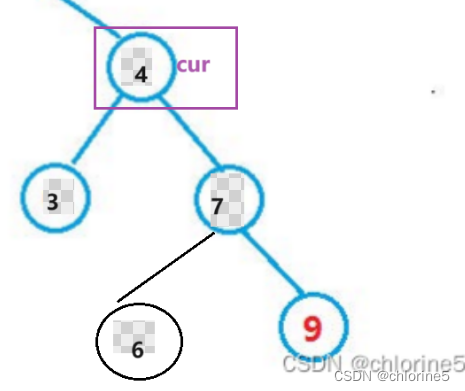
- 1. 需要使用替换法进行删除,即在它的右子树中寻找中序下的第一个结点(关键码最小),用它的值填补到被删除节点中,再来处理该结点的删除问题
要么在左树中找到最大值(左数最右边的值),要么在右数找到最小值(右数最左边值)我们最终的目的是让cur的右节点给cur,然后让cur指向cur的右树的最大值。
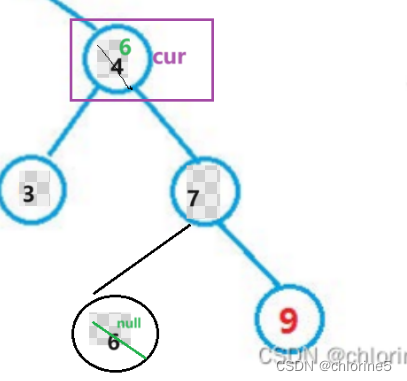
这种情况下我们就要将,6给cur,然后让原先6对应的值置空。
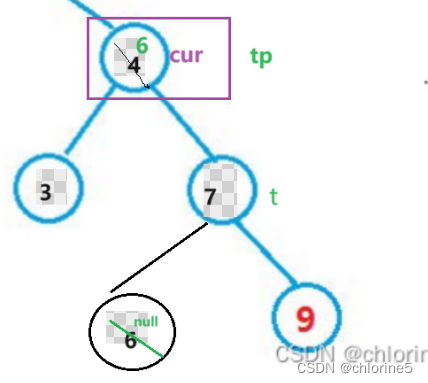
用tp记录cur的位置,然后t是tp的右孩子,为什么选择右孩子呢?因为我们要删除cur对应的值,那么我们就有俩种选择 (要么cur左边的最大值,要么cur右边的最小值)
此时我选择是找cur右边的最小值进行。
t是cur的右边,然后我们要先判断一下 是否t的左边为不为空,如果不为空,那么我们就要进入左边,因为二叉搜索树的特点就是 左孩子<根节点<右孩子,所以我们当初就是要找到cur的右边的最小值,就是一直往cur右孩子的左边找,不为空,那么我们就要将6赋值给cur,然后让置空即可。
如果下面还有值,如果右节点有值,那么就将那个右值赋值,如果左节点有值,那么就将左值赋值。
public void remove(int key){//移除之前我们需要找到这个keyTreeNode cur = root;TreeNode parent=cur;while (cur != null) {//如果值小于关键字,那么去二叉树的右边if (cur.val < key) {parent=cur;cur = cur.right;//如果值大于关键字,那么去二叉树的左边} else if (cur.val > key) {parent=cur;cur = cur.left;} else {//开始删除removeNode(cur,parent);}}}public void removeNode(TreeNode cur,TreeNode parent){if(cur.left==null){//左树空if(cur==root){root=cur.right;} else if (cur==parent.left) {parent.left=cur.right;}else{parent.right=cur.right;}//如果cur的左边空//cur在parent的左边,但是cur的左边空,那么我们将cur的右边节点给parent的左边//cur在parent的右边,但是cur的左边空,那么我们将cur的右边节点给parent的右边//(cur在parent的哪一边,就将cur左右哪一个不为空的节点给parent的哪一边)} else if (cur.right==null) {//右数空if(cur==root){root=cur.left;} else if (cur==parent.left) {parent.left=cur.left;}else {parent.right=cur.left;}//cur左边为空,那么就将cur的左边节点 要么给parent的左边,那么parent的右边//(取决于 cur在parent的哪一边)} else {//要么在左树中找到最大值(左数最右边的值)//要么在右数找到最小值(右数最左边值)//cur俩边都不为空TreeNode tp=cur;TreeNode t=cur.right;//此时的cur'是关键字,cur的左右俩边都不为空,我们要将cur的右边值给到cur// (cur右节点的左节点不为空,我们就将if(t.left!=null){tp=t;t=t.left;}cur.val=t.val;//删除t//如果t在tp左边,将t的右边值给tp左边//如果t在tp右边,将t的右边值给tp的右边if(tp.left==t){tp.left=t.right;}else{tp.right=t.right;}}}今天张老师生病了。