数据审计 -本福德定律 Benford’s law
准备工作,可以去下载 classicmodels 数据库资源如下
[ 点击:classicmodels]
也可以去我的博客资源下载
文章目录
- 数据审计 -本福德定律 Benford's law
- 前言
- 一、什么是 本福德定律?
- 二、数学公式
- 三、应用领域
- 四、应用(看看是否有 会计、审计和欺诈检测。)
- 总结
前言
假设 classicmodels 公司的 CEO 想知道 自己的 公司的数据是可能造假,于是找到了 小Tom kk 帮他分析数据。
一、什么是 本福德定律?
本福特定律,也称为本福德法则,说明一堆从实际生活得出的数据中,以1为首位数字的数的出现机率约为总数的三成,接近期望值1/9的3倍。推广来说,越大的数,以它为首几位的数出现的机率就越低。它可用于检查各种数据是否有造假。
本福特定律最早由数学家暨天文学家纽康伯(Simon Newcomb)在1881年观察到,而通用电器公司的物理学家本福特(Frank Benford)博士在1938年正式将其公开发表。这一定律因其贡献而被命名为本福特定律。本福特通过对各种数值数据的分析,确定了从1到9中以任意数字n作为第一位数的概率为log10(1+1/n)。
在我们的日常生活中,以数字1开头的数字在各个领域中出现的频率似乎要高于其他数字。这就是著名的本福特定律,也被称为“第一位数定律”或者“首位数现象”。本文将详细介绍本福特定律的历史背景、原理,并且探讨它的应用领域和实际意义。
大家可以去看 下 百度的文章,
二、数学公式
以n开头的数的出现概率为log10(1 + 1/n)。
三、应用领域
会计欺诈检测
在刑事审判中的使用
宏观经济数据
价格数字分析
基因组数据
四、应用(看看是否有 会计、审计和欺诈检测。)
也称为第一位数字定律,规定在来自许多(但不是全部)现实生活数据源的数字列表中,前导数字以特定的、不均匀的方式分布。准确地说,P(d) = log 10 (1 + 1/d),其中 d 是 1-9 范围内的数字。因此,如果您对某列有 n 个观察值,则每个数字的预期值为 n*log 10 (1 + 1/d)
编写 SQL 代码来计算 Payments 中金额第一位数字的观察值和预期值。
您需要使用卡方统计量来检验观察到的数据是否遵循本福德定律。
本福德定律
SELECT LEFT(amount,1) as Digit, COUNT(*) as Observed,
ROUND((SELECT COUNT(*) FROM Payments)*LOG10(1+1/left(amount,1)),0) as Expected
FROM Payments
GROUP BY Digit, Expected
ORDER BY Digit;
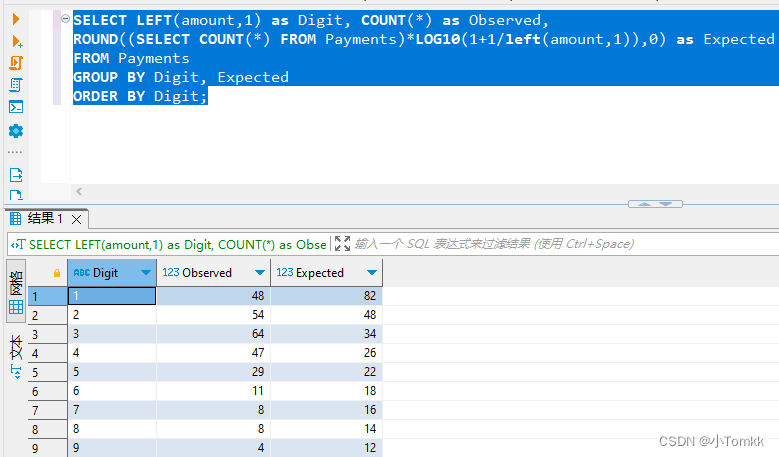
卡方统计
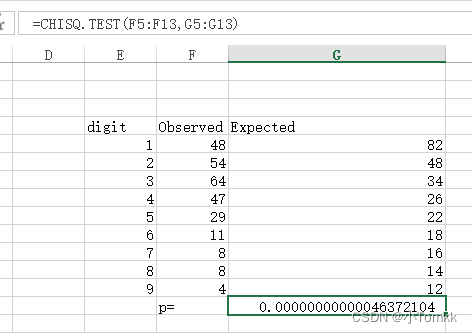
excel 永远是神器
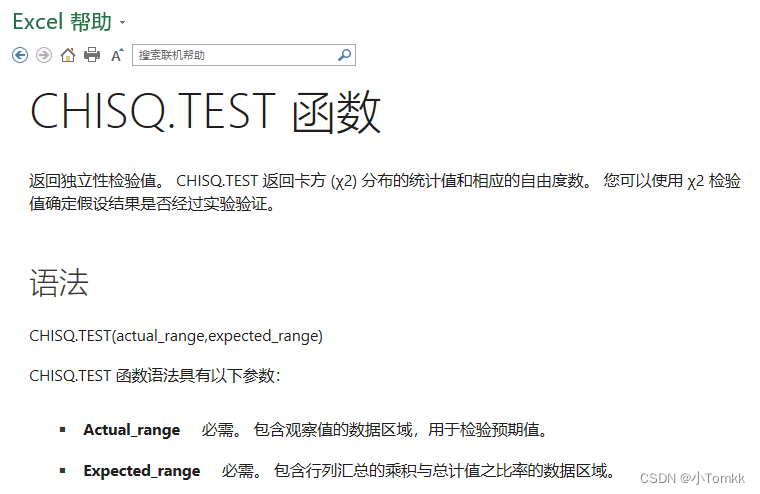

用CHISQ.TEST进行卡方检验,得到P值,如果P值小于0.05,则拒绝观察的样本跟期望的样本比例一致。
总结
本福德定律在在统计学用的比较多。特别是上市公司财报。最后谢谢大家。
希望大家喜欢 , 谢谢大家,我一直在一边面试,一边学习,一边考证,一边写作,充实自己。