[蓝桥杯 2019 省 B] 等差数列
题目描述
数学老师给小明出了一道等差数列求和的题目。但是粗心的小明忘记了一部分的数列,只记得其中 N N N 个整数。
现在给出这 N N N 个整数,小明想知道包含这 N N N 个整数的最短的等差数列有几项?
输入格式
输入的第一行包含一个整数 N N N。
第二行包含 N N N 个整数 A 1 , A 2 , ⋯ , A N A_1,A_2,\cdots,A_N A1,A2,⋯,AN。(注意 A 1 ∼ A N A_1 ∼ A_N A1∼AN 并不一定是按等差数列中的顺序给出 )。
输出格式
输出一个整数表示答案。
样例 #1
样例输入 #1
5
2 6 4 10 20
样例输出 #1
10
提示
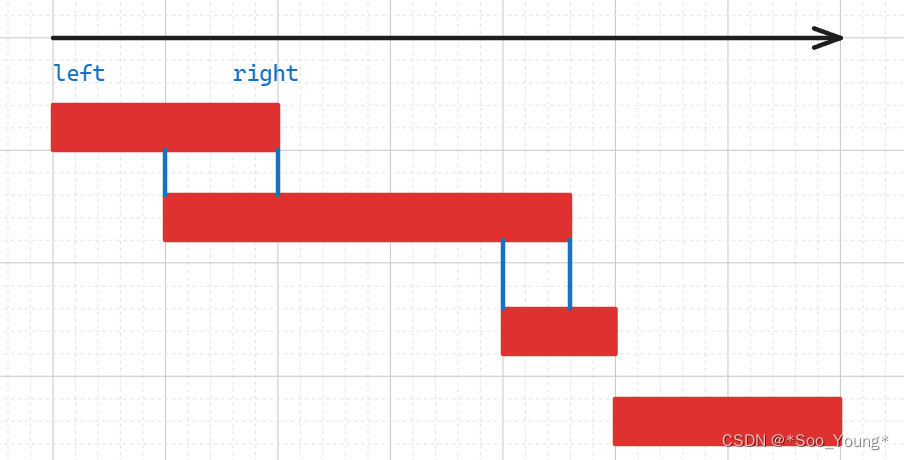
包含 2,6,4,10,20 的最短的等差数列是 2,4,6,8,10,12,14,16,18,20。
对于所有评测用例, 2 ≤ N ≤ 1 0 5 2 \le N \le 10^5 2≤N≤105, 0 ≤ A i ≤ 1 0 9 0 \le A_i \le 10^9 0≤Ai≤109。
蓝桥杯 2019 年省赛 B 组 H 题。
思路
首先,定义一些常量和变量,包括数组大小N,数组a,还有一个使用辗转相除法计算两数最大公约数的函数gcd。
接着,从输入中读取了一个整数n,然后读取了n个整数并存储在数组a中。定义了一个整数d,用来存储数组a中第二个元素和第一个元素的差值。然后对数组a进行了排序。
接下来,遍历数组a,从第三个元素开始,计算每个元素和前一个元素的差值,然后用gcd函数求出这个差值和d的最大公约数,并将结果赋值给d。
最后,如果d不为0,输出((a[n] - a[1]) / d + 1),否则输出n。
注意
需要进行特判,当公差为0时,所有数都相同,直接输出n,否则会引发除零异常。

AC代码
#include <algorithm>
#include <iostream>
#define mp make_pair
#define AUTHOR "HEX9CF"
using namespace std;
using ll = long long;const int N = 1e6 + 7;
const int INF = 0x3f3f3f3f;
const ll MOD = 1e9 + 7;int n;
int a[N];
int diff[N];int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> n;for (int i = 1; i <= n; i++) {cin >> a[i];}int dmin = INF;sort(a + 1, a + n + 1);for (int i = 2; i <= n; i++) {diff[i] = a[i] - a[i - 1];dmin = min(dmin, diff[i]);}cout << (dmin ? ((a[n] - a[1]) / dmin + 1) : n) << "\n";return 0;
}