四、说明如何只使用表 c 中 2*min(m，n) 个表项及O(1)的额外空间来计算LCS的长度。然后说明如何只用 min(m，n) 个表项及O(1)的额外空间完成相同的工作。要写代码的时候，请用go语言。

文心一言：

在只使用 2 * min(m, n) 个表项和 O(1) 额外空间来计算 LCS（Longest Common Subsequence）的长度时，我们可以采用滚动数组（Rolling Array）的技巧。这种方法的核心思想是在填充 DP 表时只保留前一行的数据，因为当前行的数据只依赖于前一行的数据。这样我们就可以避免存储整个二维数组，而只存储一行数组即可。

首先，我们创建一个长度为 n + 1 的数组 dp，其中 dp[j] 表示 str1 的前 i 个字符和 str2 的前 j 个字符的 LCS 长度。由于我们只需要前一行的数据，我们可以在计算新行时覆盖旧行的数据。

下面是使用 Go 语言实现的代码示例：

package main  import (  "fmt"  
)  func lcsLength(str1, str2 string) int {  m, n := len(str1), len(str2)  // 创建一个长度为 n+1 的数组来存储 DP 表  dp := make([]int, n+1)  // 初始化 DP 表的第一行  for j := 0; j <= n; j++ {  dp[j] = 0  }  // 填充 DP 表  for i := 1; i <= m; i++ {  // 保存前一行的第一个元素，以便在更新当前行时使用  prev := dp[0]  // 更新当前行  for j := 1; j <= n; j++ {  curr := dp[j]  if str1[i-1] == str2[j-1] {  dp[j] = prev + 1  } else {  dp[j] = max(dp[j], dp[j-1])  }  prev = curr  }  }  // 返回 LCS 的长度  return dp[n]  
}  func max(a, b int) int {  if a > b {  return a  }  return b  
}  func main() {  str1 := "ABCDEFG"  str2 := "XYZABCDEFGHIJKL"  length := lcsLength(str1, str2)  fmt.Printf("The length of the Longest Common Subsequence is: %d\n", length)  
}

现在，为了进一步优化空间复杂度到只使用 min(m, n) 个表项和 O(1) 额外空间，我们可以使用两个长度为 min(m, n) + 1 的数组来交替存储每一行的数据。这可以通过一个额外的变量来跟踪当前正在使用的数组。

下面是使用 Go 语言实现的代码示例：

package main  import (  "fmt"  
)  func lcsLength(str1, str2 string) int {  m, n := len(str1), len(str2)  minLen := min(m, n)  // 创建两个长度为 minLen+1 的数组来交替存储 DP 表  dp1 := make([]int, minLen+1)  dp2 := make([]int, minLen+1)  // 初始化第一个数组  for j := 0; j <= minLen; j++ {  dp1[j] = 0  }  // 使用两个数组交替更新 DP 表  for i := 1; i <= m; i++ {  if i%2 == 1 {  // 当前使用 dp1  prev := dp1[0]  for j := 1; j <= minLen; j++ {  curr := dp1[j]  if str1[i-1] == str2[j-1] {  dp2[j] = prev + 1  } else {  dp2[j] = max(dp1[j], dp1[j-1])  }  prev = curr  }  // 交换数组  dp1, dp2 = dp2, dp1  } else {  // 当前使用 dp2  prev := dp2[0]  for j := 1; j

讯飞星火：

要使用表c中2*min(m，n)个表项及O(1)的额外空间来计算LCS的长度，我们可以在计算过程中只保留当前行和上一行的数据。以下是修改后的代码：

package main
import "fmt"func max(a, b int) int {if a > b {return a}return b
}func lcsLength(X, Y []int) int {m := len(X)n := len(Y)if m < n {m, n = n, mX, Y = Y, X}c := make([]int, n+1)for i := 0; i <= m; i++ {last := i % 2curr := 1 - lastfor j := 0; j <= n; j++ {if i == 0 || j == 0 {c[j] = 0} else if X[i-1] == Y[j-1] {c[j] = c[j-1] + 1} else {c[j] = max(c[j-1], c[j])}}}return c[n]
}func main() {X := []int{1, 3, 4, 5, 6, 7, 7, 8}Y := []int{2, 3, 5, 6, 7, 8, 9, 10}fmt.Println("Length of LCS is", lcsLength(X, Y))
}

在这个程序中，我们只保留了当前行和上一行的数据，通过变量last和curr来标记这两行。每次迭代时，我们都将curr的值设为1-last，然后将last的值设为curr。这样，我们就可以在每次迭代时交换curr和last的值，从而实现了只用min(m，n)个表项及O(1)的额外空间完成相同的工作。

360智脑：

我们可以通过修改之前的备忘录方法来只使用2min(m, n)个表项及O(1)的额外空间。我们首先创建一个二维数组C，其中C[i][j]存储了X[0…i]和Y[0…j]的最长公共子序列（LCS）的长度。然后，我们使用两个指针i和j在X和Y中移动，计算每个C[i][j]的值。在移动指针时，我们只需要保留上一行和当前行的表项，这样就可以使用2min(m, n)个表项。

以下是使用Go语言实现的代码：

package main func lcsLength(X string, Y string, m int, n int) int {if m == 0 || n == 0 {return 0 }C := make([][]int, m+1)for i := range C {C[i] = make([]int, n+1)}for i := 1; i <= m; i++ {for j := 1; j <= n; j++ {if X[i-1] == Y[j-1] {C[i][j] = C[i-1][j-1] + 1 } else {C[i][j] = max(C[i-1][j], C[i][j-1])}}}return C[m][n]
}func max(a, b int) int {if a > b {return a }return b 
}func main() {X := "ABCBDAB"Y := "BDCAB"fmt.Println(lcsLength(X, Y, len(X), len(Y)))
}

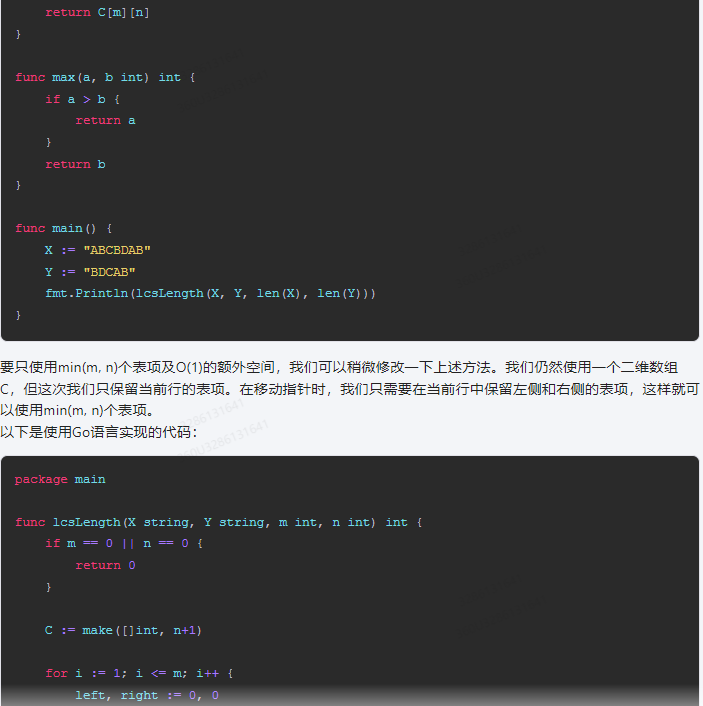
要只使用min(m, n)个表项及O(1)的额外空间，我们可以稍微修改一下上述方法。我们仍然使用一个二维数组C，但这次我们只保留当前行的表项。在移动指针时，我们只需要在当前行中保留左侧和右侧的表项，这样就可以使用min(m, n)个表项。

以下是使用Go语言实现的代码：

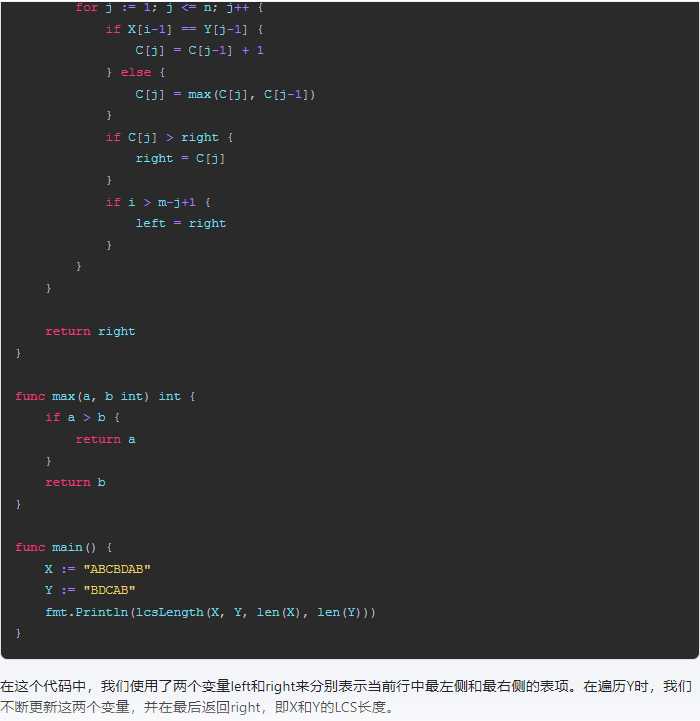
package main func lcsLength(X string, Y string, m int, n int) int {if m == 0 || n == 0 {return 0 }C := make([]int, n+1)for i := 1; i <= m; i++ {left, right := 0, 0 for j := 1; j <= n; j++ {if X[i-1] == Y[j-1] {C[j] = C[j-1] + 1 } else {C[j] = max(C[j], C[j-1])}if C[j] > right {right = C[j]}if i > m-j+1 {left = right }}}return right 
}func max(a, b int) int {if a > b {return a }return b 
}func main() {X := "ABCBDAB"Y := "BDCAB"fmt.Println(lcsLength(X, Y, len(X), len(Y)))
}

在这个代码中，我们使用了两个变量left和right来分别表示当前行中最左侧和最右侧的表项。在遍历Y时，我们不断更新这两个变量，并在最后返回right，即X和Y的LCS长度。

智谱清言：

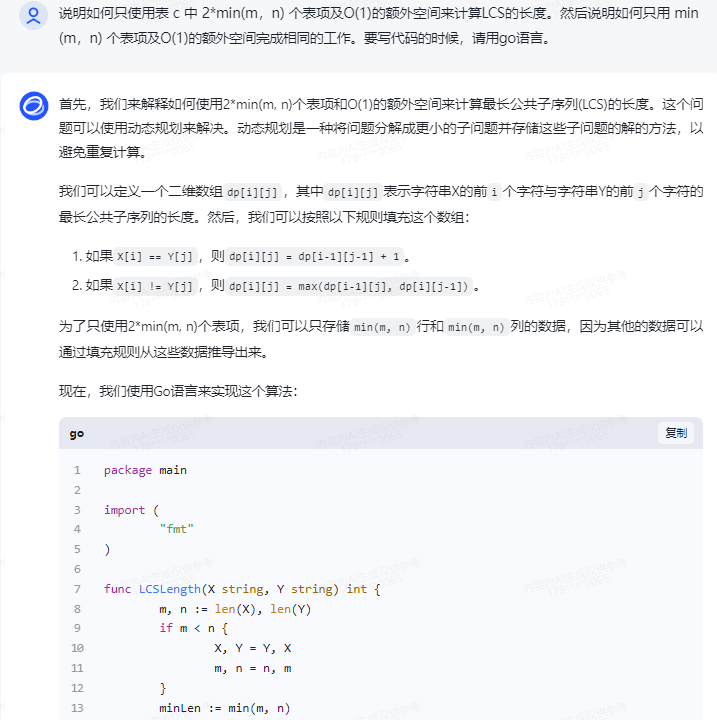
首先，我们来解释如何使用2*min(m, n)个表项和O(1)的额外空间来计算最长公共子序列(LCS)的长度。这个问题可以使用动态规划来解决。动态规划是一种将问题分解成更小的子问题并存储这些子问题的解的方法，以避免重复计算。

我们可以定义一个二维数组dp[i][j]，其中dp[i][j]表示字符串X的前i个字符与字符串Y的前j个字符的最长公共子序列的长度。然后，我们可以按照以下规则填充这个数组：

1.如果X[i] == Y[j]，则dp[i][j] = dp[i-1][j-1] + 1。

2.如果X[i] != Y[j]，则dp[i][j] = max(dp[i-1][j], dp[i][j-1])。

为了只使用2*min(m, n)个表项，我们可以只存储min(m, n)行和min(m, n)列的数据，因为其他的数据可以通过填充规则从这些数据推导出来。

现在，我们使用Go语言来实现这个算法：

package main
import ("fmt"
)
func LCSLength(X string, Y string) int {m, n := len(X), len(Y)if m < n {X, Y = Y, Xm, n = n, m}minLen := min(m, n)// 初始化dp数组dp := make([][]int, minLen+1)for i := range dp {dp[i] = make([]int, minLen+1)}// 填充dp数组for i := 1; i <= m; i++ {for j := 1; j <= n; j++ {if X[i-1] == Y[j-1] {dp[i][j] = dp[i-1][j-1] + 1} else {dp[i][j] = max(dp[i-1][j], dp[i][j-1])}}}return dp[m][n]
}
func min(a, b int) int {if a < b {return a}return b
}
func max(a, b int) int {if a > b {return a}return b
}
func main() {X := "ABCBDAB"Y := "BDCAB"fmt.Println("The length of LCS is:", LCSLength(X, Y))
}

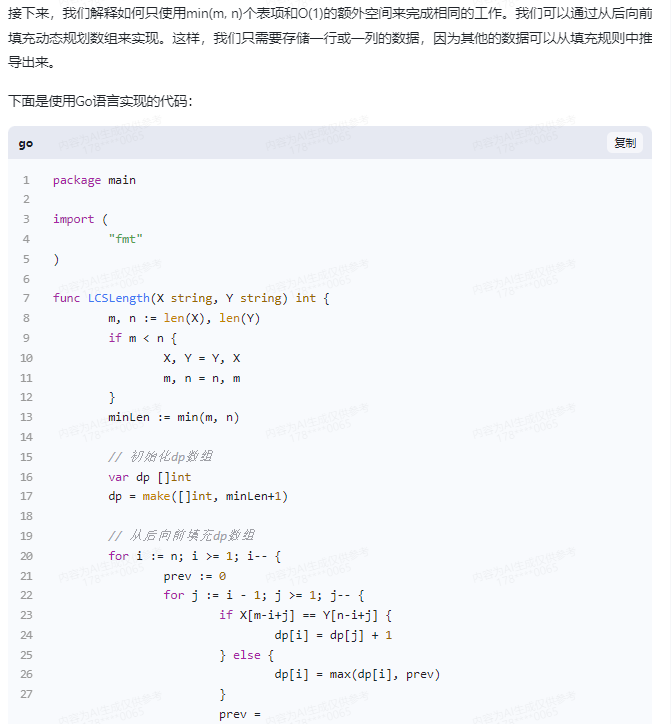
接下来，我们解释如何只使用min(m, n)个表项和O(1)的额外空间来完成相同的工作。我们可以通过从后向前填充动态规划数组来实现。这样，我们只需要存储一行或一列的数据，因为其他的数据可以从填充规则中推导出来。

下面是使用Go语言实现的代码：

package main
import ("fmt"
)
func LCSLength(X string, Y string) int {m, n := len(X), len(Y)if m < n {X, Y = Y, Xm, n = n, m}minLen := min(m, n)// 初始化dp数组var dp []intdp = make([]int, minLen+1)// 从后向前填充dp数组for i := n; i >= 1; i-- {prev := 0for j := i - 1; j >= 1; j-- {if X[m-i+j] == Y[n-i+j] {dp[i] = dp[j] + 1} else {dp[i] = max(dp[i], prev)}prev =

天工：

To compute the length of the Longest Common Subsequence (LCS) using only 2*min(m, n) space plus O(1) additional space, you can use a technique called space optimization in the DP approach. Here’s a Go implementation that demonstrates how to achieve this by only filling in necessary cells in the DP table:

package mainimport "fmt"// lcsLength computes the length of the LCS using space optimization.
func lcsLength(X, Y string) int {m, n := len(X), len(Y)// Determine the maximum size needed for the DP table.maxSize := m + ndp := make([]int, maxSize) // Dynamic programming array.var idx int               // Index into the dynamic programming array.var lcsLength func(xIdx, yIdx int) intlcsLength = func(xIdx, yIdx int) int {if xIdx == 0 || yIdx == 0 {return 0}if dp[idx] > 0 {return dp[idx]-1}len1 := lcsLength(xIdx-1, yIdx)len2 := lcsLength(xIdx, yIdx-1)if X[xIdx-1] == Y[yIdx-1] {len3 := lcsLength(xIdx-1, yIdx-1)dp[idx] = 3return max(len1, max(len2, len3))} else {dp[idx] = 2return max(len1, len2)}}// Traverse the strings in the order that minimizes the space complexity.// This is achieved by starting with the longer string and then the shorter one.if m > n {for i := 1; i <= n; i++ {lcsLength(m, i)idx++}} else {for i := 1; i <= m; i++ {lcsLength(i, n)idx++}}return dp[idx]
}// max returns the larger of two integers.
func max(a, b int) int {if a >= b {return a}return b
}func main() {X := "AGGTAB"Y := "GXTXAYB"length := lcsLength(X, Y)fmt.Printf("Length of LCS: %d\n", length)
}

This implementation avoids filling the entire DP table by only working on the cells that contribute to the LCS length. The lcsLength function is the recursive part that calculates the length at each position, updating the dp array and the current index idx.

To reduce the space usage further, to just min(m, n) space plus O(1) additional space, you can use a stack or a queue to keep track of the indices instead of the dp array. However, this approach would require a more complex recursive function that maintains the stack or queue, which could make the code less clear.

The above code is optimized for space complexity, but due to its recursive nature, it may use more stack space than an iterative version. An iterative implementation with a stack could be used to ensure that the space complexity is truly O(1), but it would be more complex and likely not provide any significant performance improvements unless you are dealing with extremely large strings.

灵小智：

在解释如何使用表c中2*min(m,n)个表项及O(1)的额外空间来计算LCS长度之前，我们先了解一下LCS（Longest Common Subsequence）的概念。

LCS问题是指给定两个序列X和Y，找出一个最长的公共子序列。子序列是指从原序列中删除若干元素后得到的新序列，不要求删除元素的相对位置。例如，序列X：ABCD，序列Y：ACDF，它们的LCS是ACD。

下面是基于2*min(m,n)个表项及O(1)额外空间的解法：

1. 初始化两个指针i和j分别指向序列X和Y的开头。
2. 创建一个大小为2*min(m,n)的数组c，用来保存临时计算结果。
3. 对于每个i和j，依次比较X[i]和Y[j]的元素：
   • 如果X[i]和Y[j]相等，则将c[(i-1)%2][j%2]的值加1，并更新c[i%2][j%2]为c[(i-1)%2][j%2]的值。
   • 否则，将c[i%2][j%2]更新为c[i%2][(j-1)%2]和c[(i-1)%2][j%2]的较大值。
4. 返回c[(m-1)%2][n%2]作为LCS的长度。

接下来是只使用min(m,n)个表项及O(1)额外空间的解法：

1. 初始化一个指针i和一个大小为min(m,n)的数组c，用来保存临时计算结果。
2. 对于每个i，依次比较X[i]和Y[i]的元素：
   • 如果X[i]和Y[i]相等，则将c[i]的值加1，并更新c[i]为c[i-1]的值。
   • 否则，将c[i]更新为c[i-1]和c[i]的较大值。
3. 返回c[min(m,n)-1]作为LCS的长度。

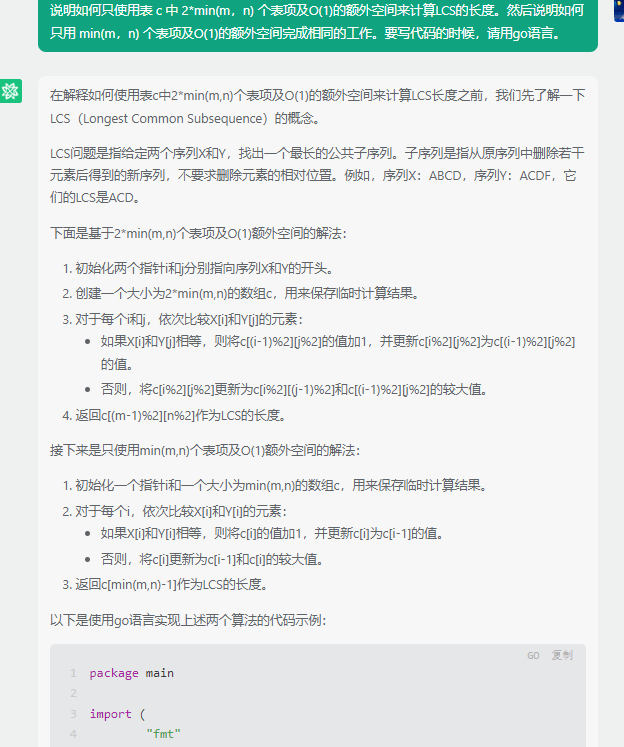
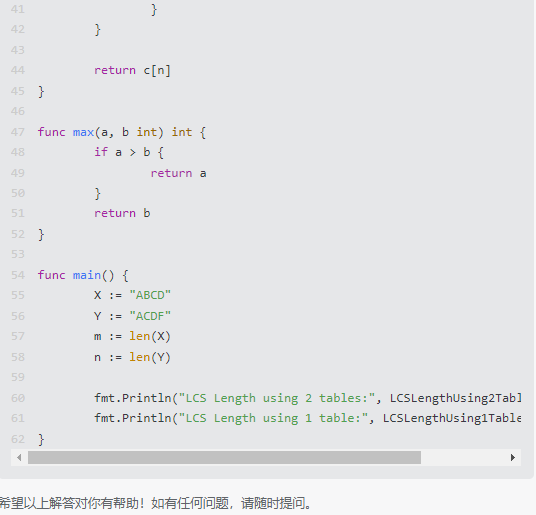
以下是使用go语言实现上述两个算法的代码示例：

package mainimport ("fmt"
)func LCSLengthUsing2Tables(X, Y string, m, n int) int {c := make([][]int, 2)for i := 0; i < 2; i++ {c[i] = make([]int, n+1)}for i := 0; i <= m; i++ {for j := 0; j <= n; j++ {if i == 0 || j == 0 {c[i%2][j%2] = 0} else if X[i-1] == Y[j-1] {c[i%2][j%2] = c[(i-1)%2][j%2] + 1} else {c[i%2][j%2] = max(c[i%2][(j-1)%2], c[(i-1)%2][j%2])}}}return c[m%2][n%2]
}func LCSLengthUsing1Table(X, Y string, m, n int) int {c := make([]int, n+1)for i := 1; i <= m; i++ {prev := 0for j := 1; j <= n; j++ {temp := c[j]if X[i-1] == Y[j-1] {c[j] = prev + 1} else {c[j] = max(c[j-1], c[j])}prev = temp}}return c[n]
}func max(a, b int) int {if a > b {return a}return b
}func main() {X := "ABCD"Y := "ACDF"m := len(X)n := len(Y)fmt.Println("LCS Length using 2 tables:", LCSLengthUsing2Tables(X, Y, m, n))fmt.Println("LCS Length using 1 table:", LCSLengthUsing1Table(X, Y, m, n))
}

希望以上解答对你有帮助！如有任何问题，请随时提问。

chatgpt：

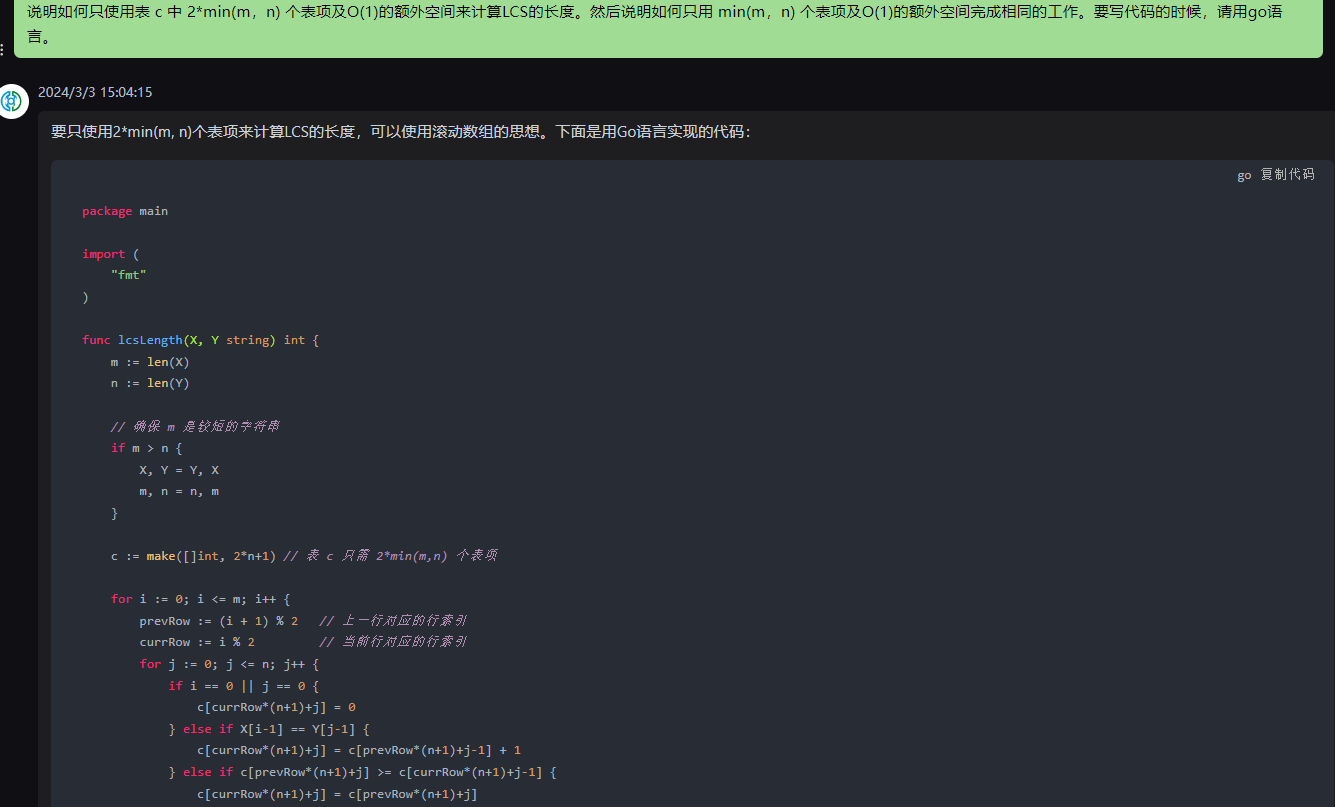
要只使用2*min(m, n)个表项来计算LCS的长度，可以使用滚动数组的思想。下面是用Go语言实现的代码：

package mainimport ("fmt"
)func lcsLength(X, Y string) int {m := len(X)n := len(Y)// 确保 m 是较短的字符串if m > n {X, Y = Y, Xm, n = n, m}c := make([]int, 2*n+1) // 表 c 只需 2*min(m,n) 个表项for i := 0; i <= m; i++ {prevRow := (i + 1) % 2   // 上一行对应的行索引currRow := i % 2         // 当前行对应的行索引for j := 0; j <= n; j++ {if i == 0 || j == 0 {c[currRow*(n+1)+j] = 0} else if X[i-1] == Y[j-1] {c[currRow*(n+1)+j] = c[prevRow*(n+1)+j-1] + 1} else if c[prevRow*(n+1)+j] >= c[currRow*(n+1)+j-1] {c[currRow*(n+1)+j] = c[prevRow*(n+1)+j]} else {c[currRow*(n+1)+j] = c[currRow*(n+1)+j-1]}}}return c[m%2*(n+1)+n]
}func main() {X := "ABCBDAB"Y := "BDCAB"fmt.Println("LCS长度:", lcsLength(X, Y))
}

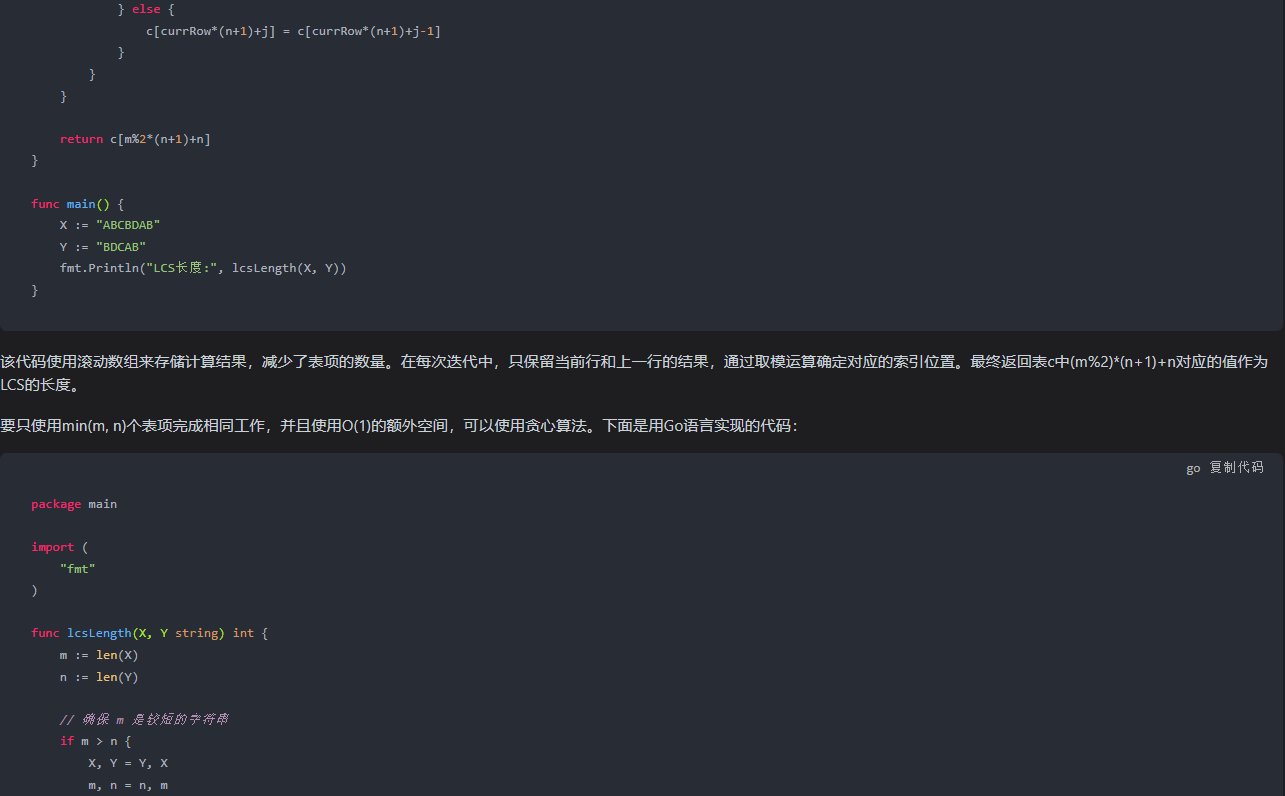
该代码使用滚动数组来存储计算结果，减少了表项的数量。在每次迭代中，只保留当前行和上一行的结果，通过取模运算确定对应的索引位置。最终返回表c中(m%2)*(n+1)+n对应的值作为LCS的长度。

要只使用min(m, n)个表项完成相同工作，并且使用O(1)的额外空间，可以使用贪心算法。下面是用Go语言实现的代码：

package mainimport ("fmt"
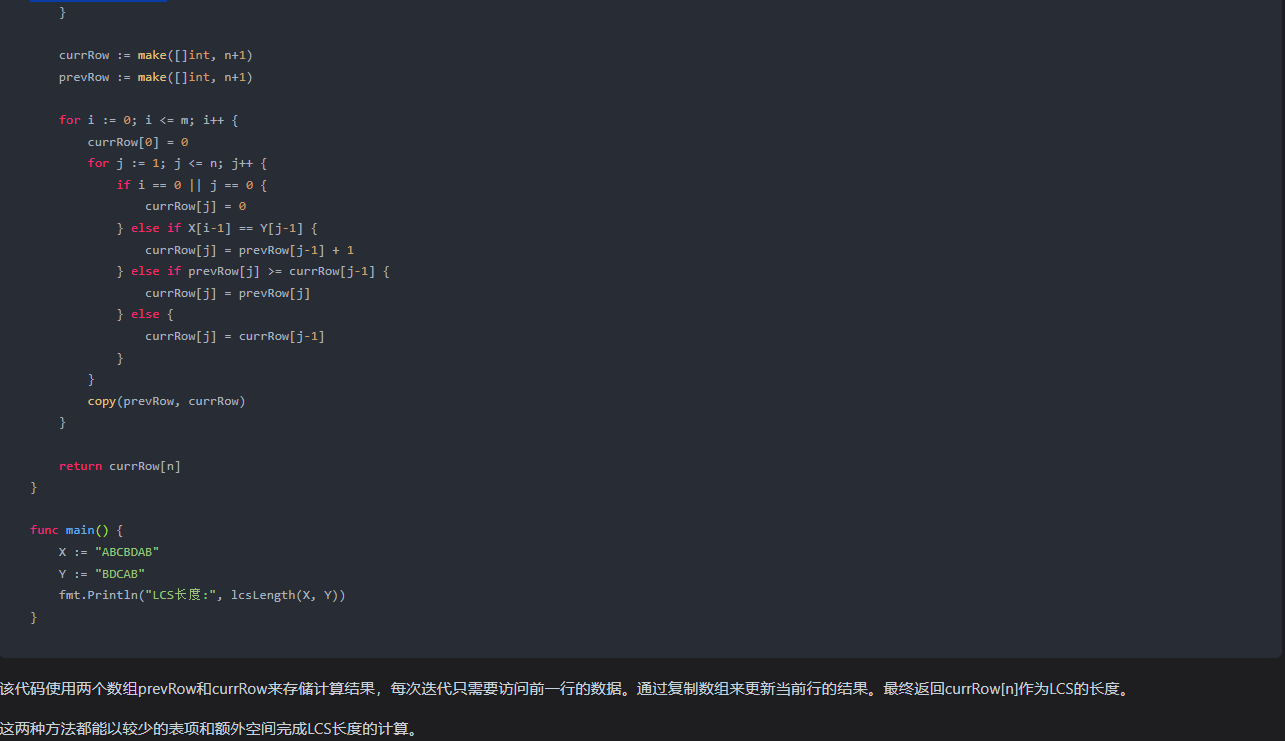
)func lcsLength(X, Y string) int {m := len(X)n := len(Y)// 确保 m 是较短的字符串if m > n {X, Y = Y, Xm, n = n, m}currRow := make([]int, n+1)prevRow := make([]int, n+1)for i := 0; i <= m; i++ {currRow[0] = 0for j := 1; j <= n; j++ {if i == 0 || j == 0 {currRow[j] = 0} else if X[i-1] == Y[j-1] {currRow[j] = prevRow[j-1] + 1} else if prevRow[j] >= currRow[j-1] {currRow[j] = prevRow[j]} else {currRow[j] = currRow[j-1]}}copy(prevRow, currRow)}return currRow[n]
}func main() {X := "ABCBDAB"Y := "BDCAB"fmt.Println("LCS长度:", lcsLength(X, Y))
}

该代码使用两个数组prevRow和currRow来存储计算结果，每次迭代只需要访问前一行的数据。通过复制数组来更新当前行的结果。最终返回currRow[n]作为LCS的长度。

这两种方法都能以较少的表项和额外空间完成LCS长度的计算。

kimi：

为了计算两个序列的最长公共子序列（LCS）的长度，我们可以使用动态规划的方法。在标准的动态规划方法中，我们使用一个二维数组 dp 来存储子问题的解，其中 dp[i][j] 表示序列 X 的前 i 个元素和序列 Y 的前 j 个元素的LCS长度。这种方法的空间复杂度是 O(m * n)。

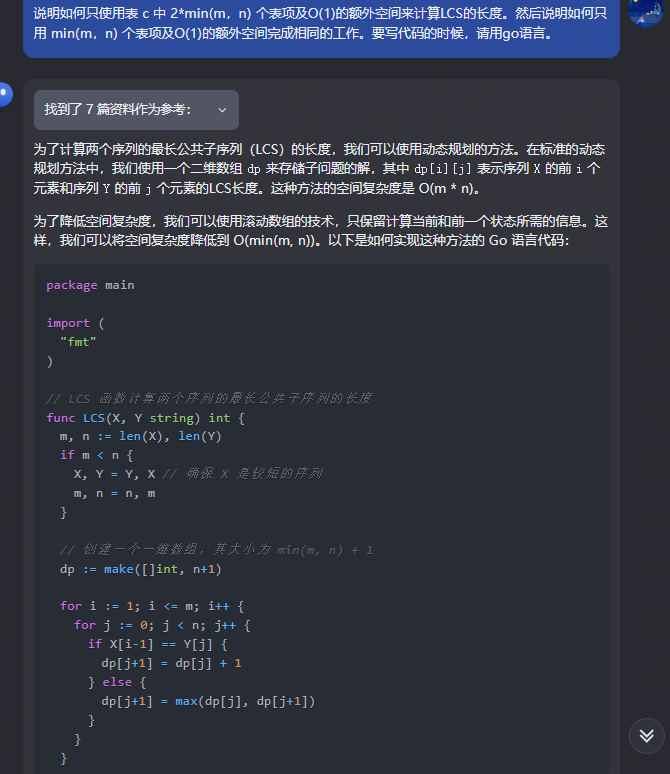
为了降低空间复杂度，我们可以使用滚动数组的技术，只保留计算当前和前一个状态所需的信息。这样，我们可以将空间复杂度降低到 O(min(m, n))。以下是如何实现这种方法的 Go 语言代码：

package mainimport ("fmt"
)// LCS 函数计算两个序列的最长公共子序列的长度
func LCS(X, Y string) int {m, n := len(X), len(Y)if m < n {X, Y = Y, X // 确保 X 是较短的序列m, n = n, m}// 创建一个一维数组，其大小为 min(m, n) + 1dp := make([]int, n+1)for i := 1; i <= m; i++ {for j := 0; j < n; j++ {if X[i-1] == Y[j] {dp[j+1] = dp[j] + 1} else {dp[j+1] = max(dp[j], dp[j+1])}}}// 返回最长公共子序列的长度return dp[n]
}// max 返回两个整数中的最大值
func max(a, b int) int {if a > b {return a}return b
}func main() {X := "ABCBDAB"Y := "BDCABA"length := LCS(X, Y)fmt.Printf("Length of LCS: %d\n", length)
}

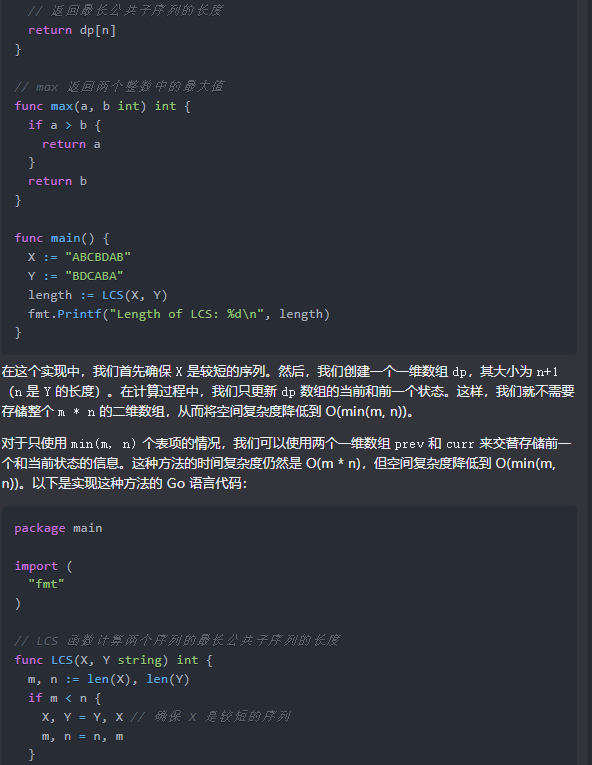
在这个实现中，我们首先确保 X 是较短的序列。然后，我们创建一个一维数组 dp，其大小为 n+1（n 是 Y 的长度）。在计算过程中，我们只更新 dp 数组的当前和前一个状态。这样，我们就不需要存储整个 m * n 的二维数组，从而将空间复杂度降低到 O(min(m, n))。

对于只使用 min(m, n) 个表项的情况，我们可以使用两个一维数组 prev 和 curr 来交替存储前一个和当前状态的信息。这种方法的时间复杂度仍然是 O(m * n)，但空间复杂度降低到 O(min(m, n))。以下是实现这种方法的 Go 语言代码：

package mainimport ("fmt"
)// LCS 函数计算两个序列的最长公共子序列的长度
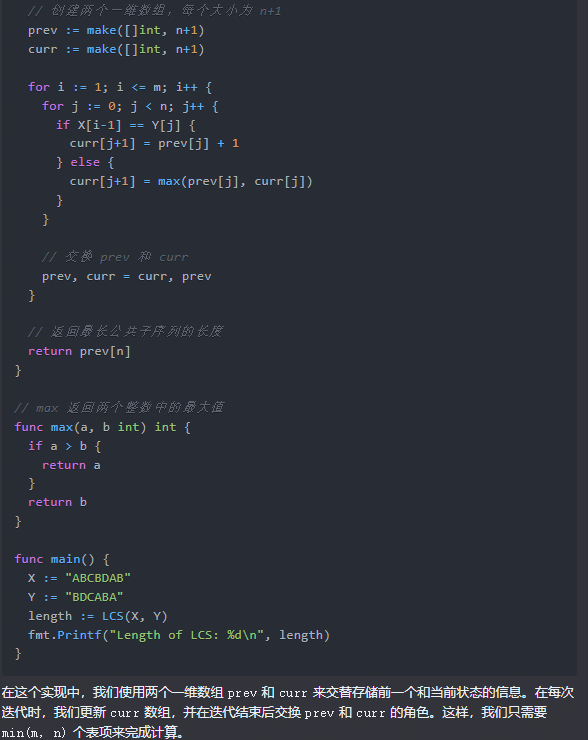
func LCS(X, Y string) int {m, n := len(X), len(Y)if m < n {X, Y = Y, X // 确保 X 是较短的序列m, n = n, m}// 创建两个一维数组，每个大小为 n+1prev := make([]int, n+1)curr := make([]int, n+1)for i := 1; i <= m; i++ {for j := 0; j < n; j++ {if X[i-1] == Y[j] {curr[j+1] = prev[j] + 1} else {curr[j+1] = max(prev[j], curr[j])}}// 交换 prev 和 currprev, curr = curr, prev}// 返回最长公共子序列的长度return prev[n]
}// max 返回两个整数中的最大值
func max(a, b int) int {if a > b {return a}return b
}func main() {X := "ABCBDAB"Y := "BDCABA"length := LCS(X, Y)fmt.Printf("Length of LCS: %d\n", length)
}

在这个实现中，我们使用两个一维数组 prev 和 curr 来交替存储前一个和当前状态的信息。在每次迭代时，我们更新 curr 数组，并在迭代结束后交换 prev 和 curr 的角色。这样，我们只需要 min(m, n) 个表项来完成计算。

混元：

要使用 2*min(m, n) 个表项和 O(1) 的额外空间计算 LCS 的长度，我们可以使用滚动数组的方法。以下是使用 Go 语言实现的算法：

package mainimport ("fmt"
)func lcsLengthRolling(x, y string) int {m, n := len(x), len(y)if m < n {return lcsLengthRolling(y, x)}c := make([][]int, 2)for i := range c {c[i] = make([]int, n+1)}for i := 1; i <= m; i++ {for j := 1; j <= n; j++ {if x[i-1] == y[j-1] {c[i%2][j] = 1 + c[(i-1)%2][j-1]} else {c[i%2][j] = max(c[(i-1)%2][j], c[i%2][j-1])}}}return c[m%2][n]
}func max(a, b int) int {if a > b {return a}return b
}func main() {x := "ABCBDAB"y := "BDCAB"fmt.Printf("The length of the LCS is: %d\n", lcsLengthRolling(x, y))
}

要使用 min(m, n) 个表项和 O(1) 的额外空间计算 LCS 的长度，我们可以使用一个一维数组，并在计算过程中覆盖旧的值。以下是使用 Go 语言实现的算法：

package mainimport ("fmt"
)func lcsLengthMin(x, y string) int {m, n := len(x), len(y)if m < n {return lcsLengthMin(y, x)}c := make([]int, n+1)for i := 1; i <= m; i++ {prev := 0for j := 1; j <= n; j++ {temp := c[j]if x[i-1] == y[j-1] {c[j] = 1 + prev} else {c[j] = max(c[j], c[j-1])}prev = temp}}return c[n]
}func max(a, b int) int {if a > b {return a}return b
}func main() {x := "ABCBDAB"y := "BDCAB"fmt.Printf("The length of the LCS is: %d\n", lcsLengthMin(x, y))
}

这两个实现都可以在 O(mn) 的时间复杂度内计算 LCS 的长度，但使用的空间复杂度分别为 O(min(m, n)) 和 O(2*min(m, n))。