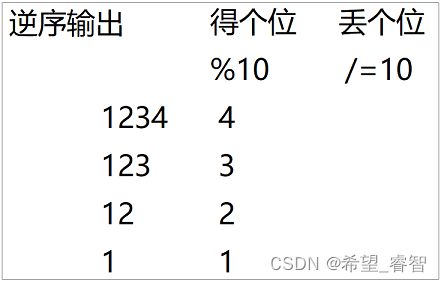
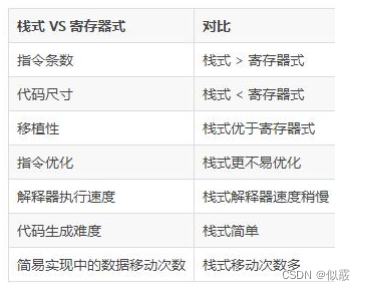
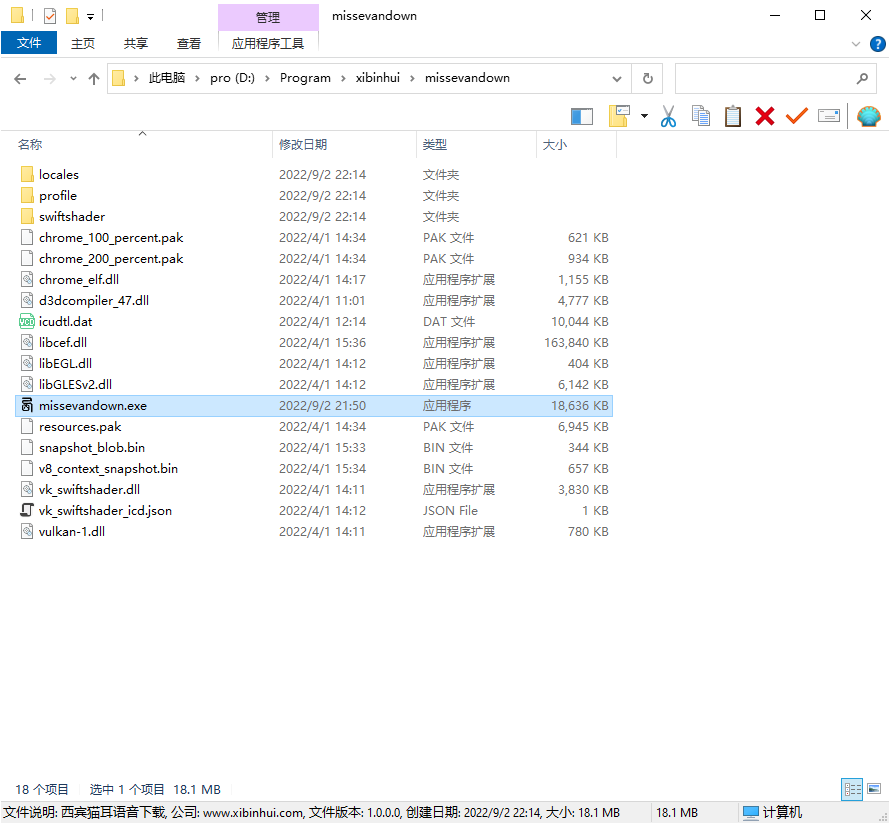
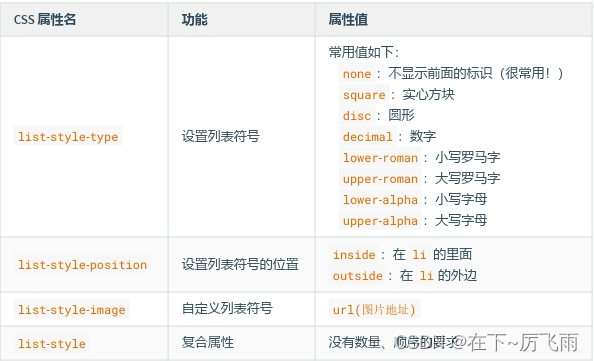
91. 解码方法 - 力扣（LeetCode）

同理：60也无法解码 

1、状态表示：

根据经验 + 题目要求：以i位置为结尾，然后”巴拉巴拉“。则dp[i]表示，以i位置为结尾时，解码方法的总数。

2、状态转移方程：

根据最近的一步，划分问题

两种情况：

1、s[i]位置，单独去解码：又分两种情况：解码成功（1 <= s[i] <= 9），解码失败（s[i] == 0）。解码成功：dp[i] 就= dp[i-1]；

解码失败：dp[i] = 0。

2、<s[i],s[i-1]>一起解码，又分两种情况：解码成功(10<= <s[i-1],s[i]> <=  26)，解码失败（<s[i],s[i-1]> == 00 || <s[i],s[i-1] > 26）。

解码成功：dp[i] = dp[i-2]。

解码失败：dp[i] = 0。

那么最终dp[i] = 两种情况之和。

3、初始化：

初始化就是为了填表时不要越界。

dp[0] = 1( 1<=s[0] <= 9)，或者dp[0] = 0 (s[0] == 0)。 

dp[1] = 0,1,2。（1：只能依次解码或者只能联合解码。2：可以依次解码，也可以联合解码。0：无法解码）。

4、填表顺序：从左往右

5、返回值：

dp[s.size()-1]。

class Solution {
public:int exchange(char a,char b)//两个数字一起解码{int sum = (a-'0')*10 + (b-'0');return sum;}int numDecodings(string s) {int n = s.size();vector<int> dp(n);//dp表，所有dp都为0了dp[0] = s[0] != '0';//初始化dp[0]，若s[0]可以解码，dp[0] = 1，反之dp[0] = 0;if( n == 1) return dp[0];//边界越界检查if(s[0] != '0' && s[1] !='0') dp[1] +=1;//初始化dp[1]，若0,1各自解码，dp[1]+1;int t = exchange(s[0],s[1]);if(t >= 10 && t <= 26) dp[1]+=1;//06这种情况无效,0,1一起解码,dp[1] +1;for(int i = 2;i<n;i++){if(s[i] != '0') dp[i] += dp[i-1];//s[i]单独解码成功，dp[i]+=dp[i-1]。int tt = exchange(s[i-1],s[i]);if(tt >= 10 && tt <= 26) dp[i] += dp[i-2];//s[i-1]和s[i]一起解码成功，dp[i]+=dp[i-2]}return dp[n-1];}
};