46、Numpy手推共空间模式CSP，用于脑电EEG信号分类-编程知识

一、Numpy实现CSP公式及对应的代码

CSP全部流程：

1、CSP先将数据按照类别分类，两类数据可分为E1、E2

2、计算分类后的原始数据的协方差矩阵：

方差矩阵：

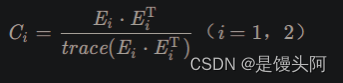
C协方差矩阵，E原始EEG信号，trace求迹

实现代码：

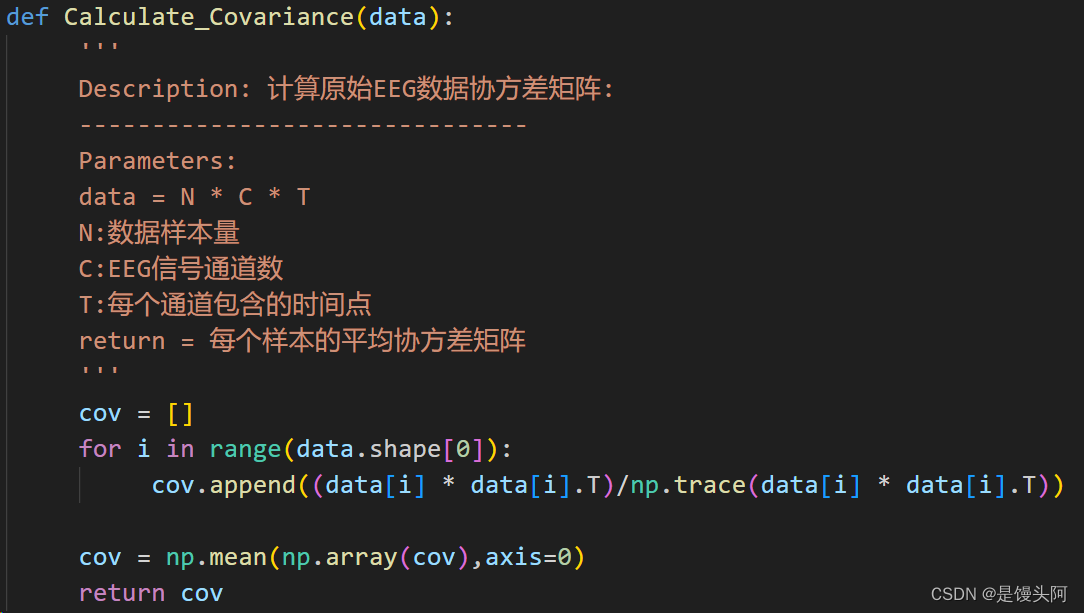
1、定义了一个计算切好段的EEG数据的平均协方差矩阵的函数：数据输入三维度：N*C*T

2、然后使用一个空列表cov，通过for循环，对数据每个样本计算协方差矩阵，并使用cov空列表保存计算的矩阵

知识点：数组的转置a.T，数组求迹：np.trace()

3、最后先使用np.array()将列表cov转为numpy格式，再用np.mean()计算cov中每个样本的协方差的均值，在x轴上计算

4、返回cov平均协方差数组

2.2 求协方差矩阵cov的特征值，特征向量：

这里定义一个函数，用于求cov的特征值和特征向量，用于后面的正交白化变换需要的特征向量矩阵、特征值对角阵、特征值（以上皆降序排列）

代码：

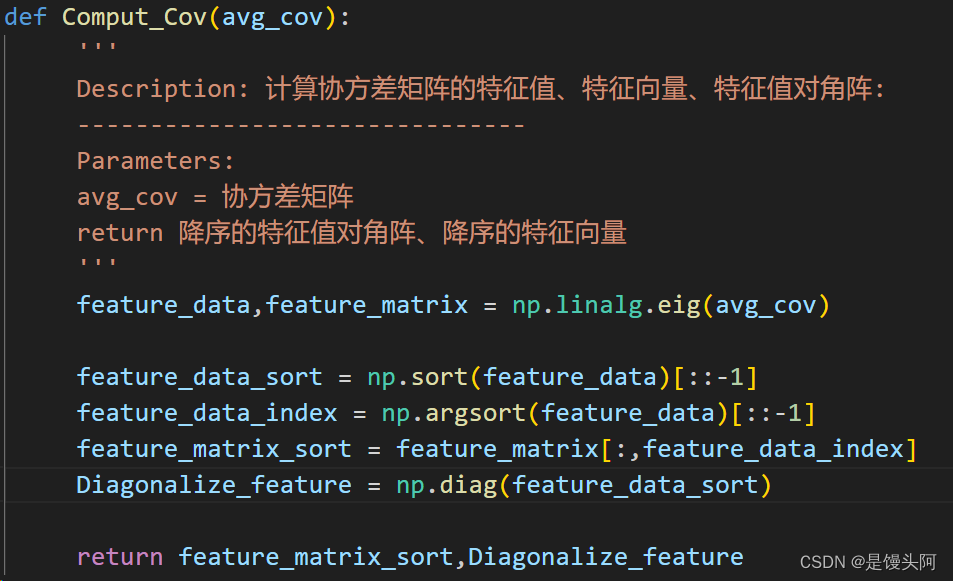
1、求要处理的目标：样本的平均协方差，记为avg_cov

2、使用np.linalg.eig()函数求avg_cov的特征值、特征向量

3、使用no.sort()对特征值进行升序排序，再使用索引[::-1]设置为降序排序

4、使用np.argsort()函数求降序排列的特征值对应的索引输出

5、使用第四步求出的降序索引，对特征值对应的特征向量进行降序排序

6、使用np.diag()求降序的特征向量对应的对角阵

补充：numpy的线性代数函数：

估计线性模型中的系数：a=np.linalg.lstsq(x,b),有b=a*x

求方阵的逆矩阵np.linalg.inv(A)

求广义逆矩阵：np.linalg.pinv(A)

求矩阵的行列式：np.linalg.det(A)

解形如AX=b的线性方程组：np.linalg.solve(A,b)

求矩阵的特征值：np.linalg.eigvals（A）

求特征值和特征向量：np.linalg.eig(A)

Svd分解：np.linalg.svd(A)

3、正交白化变换P:

在上一步函数中，我们得到了每个类别的平均协方差对应的降序的特征值和特征向量，在这里定义一个函数，直接调用这两个值建立公式即可.

3.1 计算白化矩阵P：

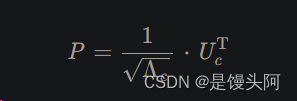
P白化矩阵，U c特征向量矩阵，Λ c 特征值对角阵

代码:

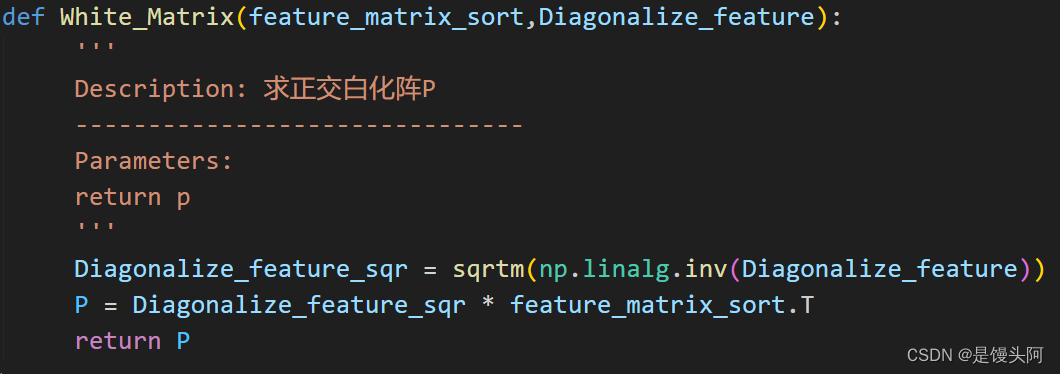
1、使用numpy的linalg子模块的inv函数求特征值对角阵的逆

2、使用scipy的linalg子模块的sqrtm函数对矩阵开平方

注：np.linalg子模块没有sqrt（对元素开平方）、sqrtm（对矩阵开）的功能

图解：

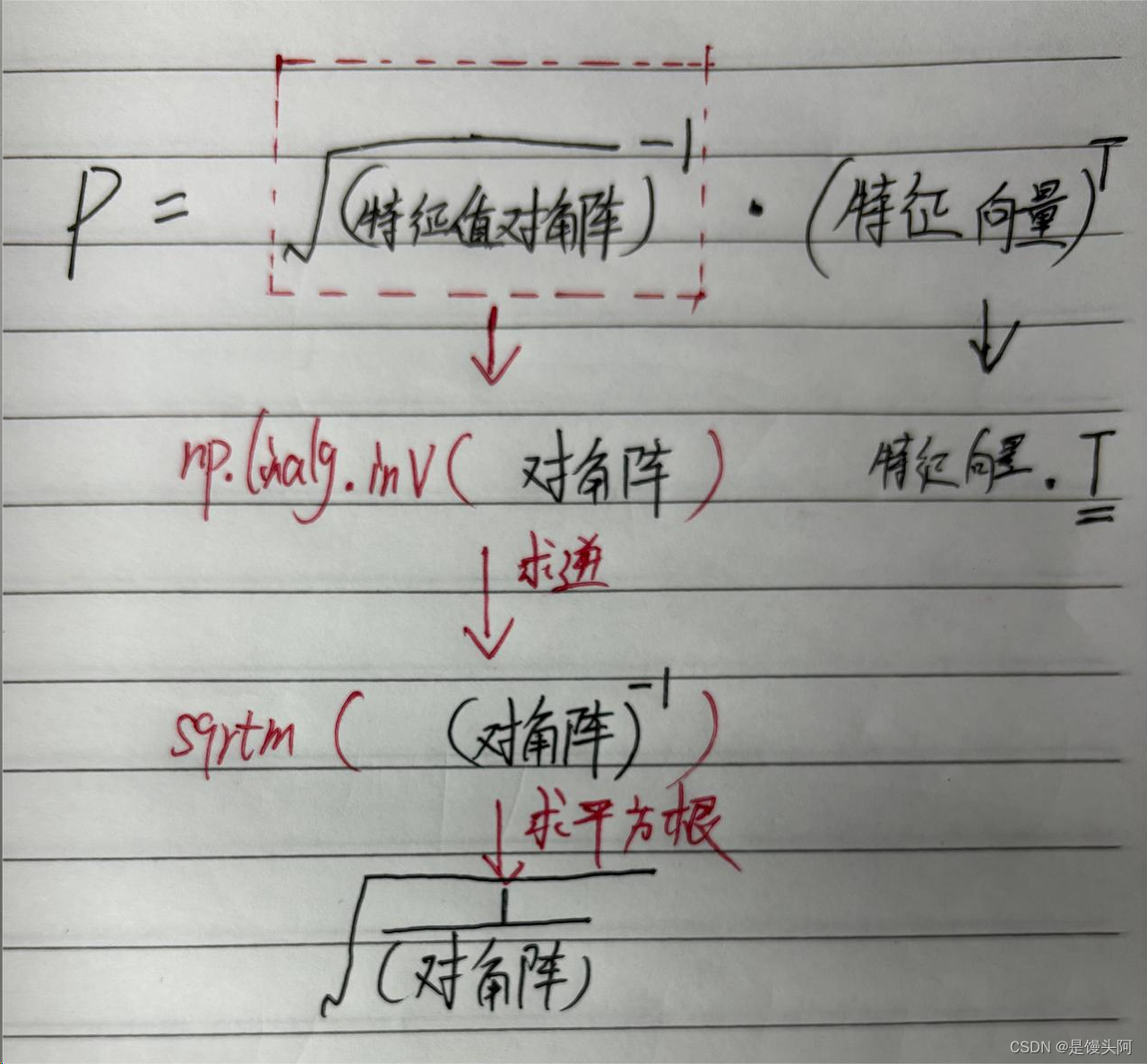
3.2 为计算投影矩阵做准备

求出白化矩阵阵P后，将P作用于脑电信号每一类别数据的平均协方差矩阵avg_cov()有：

S = P * avg_cov() * P.T

对应的公式：

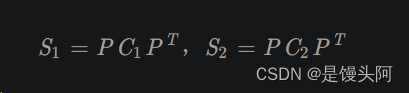
代码：

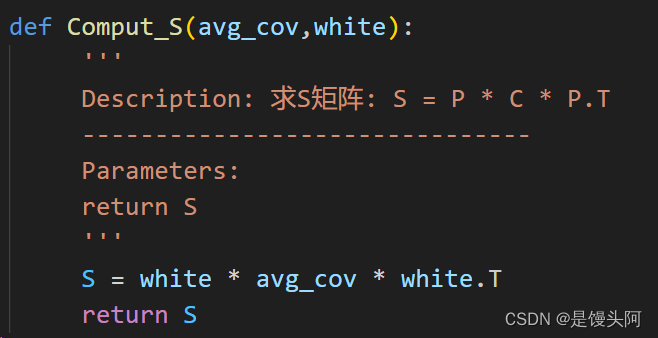
求一个类别的S矩阵的2个不同顺序的特征向量：

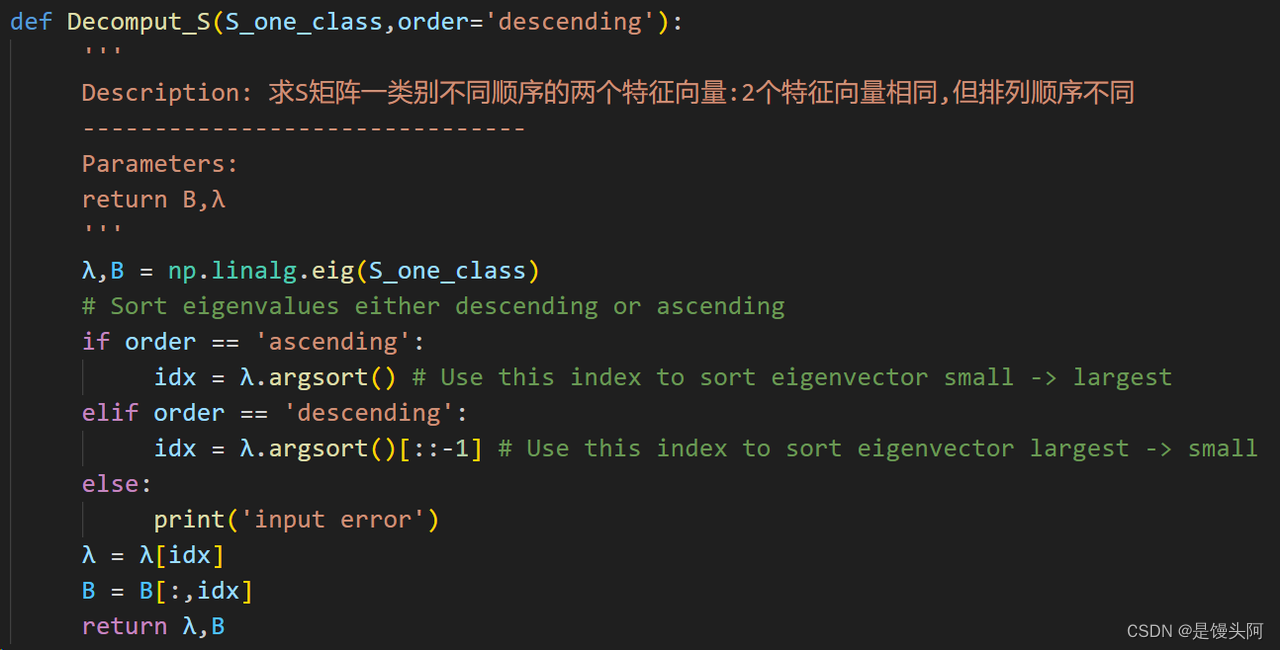
1、使用np.linalg.eig()函数求S一个类别的特征值λ,特征向量B

2、使用判断语句if从特征值λ中求两个大小相反顺序排列的索引idx

3、根据2个索引，得到大小排列顺序不同的2个矩阵λ,B（这里求特征矩阵的方式和2.2函数相同）

4、计算投影矩阵W：

对于特征向量B，当一个类别的S1矩阵有最大特征值时，此时另一个类别（2分类的话）应当有最小特征值，因此可以使用矩阵B实现两分类问题，可以得到

4.1 投影矩阵：

4.2 计算投影矩阵W的特征矩阵Z：

公式：

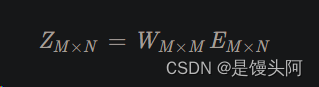
Z = 特征矩阵 W：投影矩阵 E：原始脑电数据

代码实现：

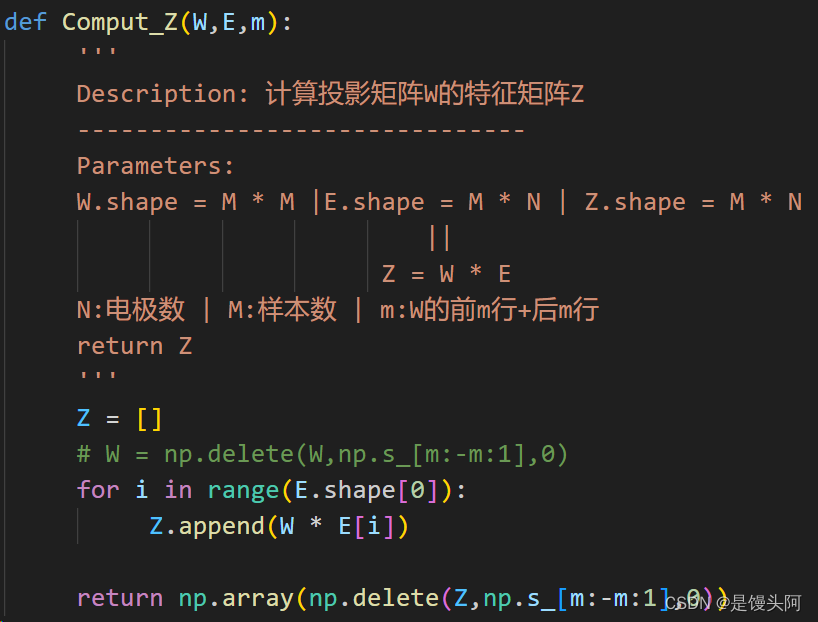
1、建立一个空列表Z，来保存后面处理好的数据

2、使用for循环，在原始EEG数据矩阵E的第一个维度进行循环遍历

3、使用list.append()函数装入W * E[i]循环相乘的矩阵，得到特征矩阵E

4、对E使用np.delete(array,obj,axis)函数,在横轴x上删除m，-m之间的元素，原因：

算法生成的CSP特征矩阵E，其信息不是等效的。特征信息主要集中在特征矩阵的头部和尾部，而中间的特征信息不明显，是可以忽略的，所以选取m行和后m行数据作为CSP特征提取的最终特征矩阵E。

注意：需要2m<M

我看到也有人先对W这样做，Z就不用做了，但CSP原论文是对E做

其中np.s_[m:-m:0]作用：

numpy中的c_、r_、s_不能称为函数，它只是CClass类的一个实例，而CClass是定义了切片方法__getitem__的类,

所以c_、r_、s_就可以对数组进行切片并按不同维度进行2个数组的链接

np.c_():切片并在y轴（列）链接

np.r_():切片并在x轴（行）链接

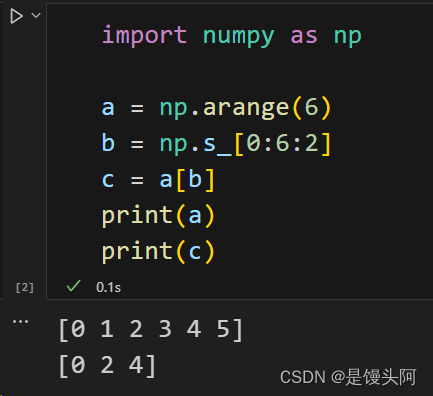
np.s_(x:y:z):生成python内置的 slice 函数，并设置 (start, stop ,step) 参数，例：

4.3 计算矩阵Z的特征值，并对其归一化：

公式：

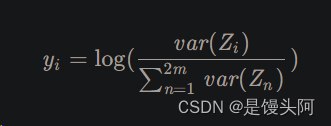
代码：

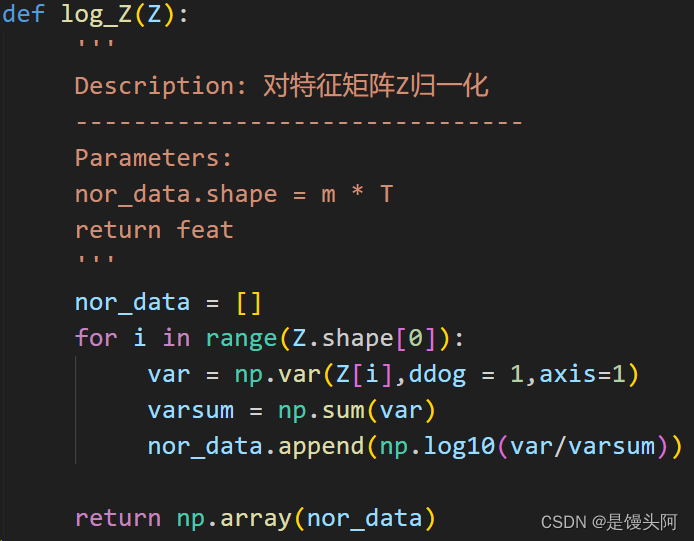
1、定义空列表nor_data用于存数据

2、for循环遍历特征矩阵Z的第一个维度

3、np.var()函数求Z的方差

4、np.sum()函数求方差和

5、np.log10()求var/varsum的log值

6、最后list.append()保存log值，并np.array()转为数组

最终我们得到了原始EEG信号的投影矩阵的归一化的特征矩阵E的前m和后m行矩阵数据，作为原始数据的输入特征

5、实现一个CSP的类吧~

以上定义的函数用来Class一个CSP的类，代码：

import numpy as np
from scipy.linalg import inv,sqrtm
import torch
from sklearn.svm import SVC,NuSVC,LinearSVC
from sklearn.metrics import classification_report, accuracy_score
from sklearn.model_selection import cross_val_score, GridSearchCV, KFold
from numpy import *
from sklearn.pipeline import make_pipeline
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
import matplotlib.pyplot as pltdef compute_cov(EEG_data):'''INPUT:EEG_data : EEG_data in shape T x N x SOUTPUT:avg_cov : covariance matrix of averaged over all trials'''cov = []for i in range(EEG_data.shape[0]):cov.append(EEG_data[i]@EEG_data[i].T/np.trace(EEG_data[i]@EEG_data[i].T))cov = np.mean(np.array(cov), 0)return cov
# def Calculate_Covariance(data):
#      '''
#      Description: 计算原始EEG数据协方差矩阵:
#      -------------------------------
#      Parameters:
#      data = N * C * T
#      N:数据样本量
#      C:EEG信号通道数
#      T:每个通道包含的时间点
#      return = 每个样本的平均协方差矩阵
#      '''
#      cov = []
#      for i in range(data.shape[0]):
#           cov.append((data[i] * data[i].T)/np.trace(data[i] * data[i].T))#      cov = np.mean(np.array(cov),axis=0)
#      return covdef Comput_Cov(avg_cov):'''Description: 计算协方差矩阵的特征值、特征向量、特征值对角阵:-------------------------------Parameters:avg_cov = 协方差矩阵return 降序的特征值对角阵、降序的特征向量'''feature_data,feature_matrix = np.linalg.eig(avg_cov) feature_data_sort = np.sort(feature_data)[::-1]feature_data_index = np.argsort(feature_data)[::-1]feature_matrix_sort = feature_matrix[:,feature_data_index]Diagonalize_feature = np.diag(feature_data_sort)return feature_matrix_sort,Diagonalize_featuredef White_Matrix(feature_matrix_sort,Diagonalize_feature):'''Description: 求正交白化阵P-------------------------------Parameters:return p'''Diagonalize_feature_sqr = sqrtm(np.linalg.inv(Diagonalize_feature))P = Diagonalize_feature_sqr@feature_matrix_sort.Treturn Pdef Comput_S(avg_cov,white):'''Description: 求S矩阵: S = P * C * P.T-------------------------------Parameters:return S'''S = white@avg_cov@white.Treturn Sdef Decomput_S(S_one_class,order='descending'):'''Description: 求S矩阵一类别不同顺序的两个特征向量:2个特征向量相同,但排列顺序不同-------------------------------Parameters:return B,λ '''λ,B = np.linalg.eig(S_one_class)# Sort eigenvalues either descending or ascendingif order == 'ascending':idx = λ.argsort() # Use this index to sort eigenvector small -> largestelif order == 'descending':idx = λ.argsort()[::-1] # Use this index to sort eigenvector largest -> smallelse:print('input error')λ = λ[idx]B = B[:,idx]return λ,Bdef Projection_W(B,P):'''Description: 计算投影矩阵W = B.T * P-------------------------------Parameters:return W'''return (B.T@P)def Comput_Z(W,E):'''Description: 计算投影矩阵W的特征矩阵Z-------------------------------Parameters:W.shape = M * M |E.shape = M * N | Z.shape = M * N ||Z = W * EN:电极数 | M:样本数 | m:W的前m行+后m行return Z'''Z = []for i in range(E.shape[0]):Z.append(W@E[i])return np.array(np.delete(Z,np.s_[3:-3:1],0))def log_Z(Z):'''Description: 对特征矩阵Z归一化-------------------------------Parameters:nor_data.shape = m * T return feat'''nor_data = []for i in range(Z.shape[0]):var = np.var(Z[i],axis=1)varsum = np.sum(var)nor_data.append(np.log10(var/varsum))return np.array(nor_data)# class My_CSP():
#      def __init__(self,m=2):
#           super(My_CSP,self).__init__()
#           self.m = m
#           self.M = None#      def fit(self,x_train,y_train):
#           #分类别，E1，E2
#           x_train_left = x_train[y_train==0]
#           x_train_right = x_train[y_train==1]
#           # 计算协方差矩阵，avg_cov
#           cov_left = Calculate_Covariance(x_train_left)
#           cov_right = Calculate_Covariance(x_train_right)
#           avg_cov = cov_left+cov_right
#           # 计算白化变换矩阵，P
#           eigval,eigve = Comput_Cov(avg_cov)
#           P = White_Matrix(eigval,eigve)
#           # 计算S矩阵+S的两个不同排列顺序的特征向量
#           S_left = Comput_S(cov_left,P)
#           S_right = Comput_S(cov_right,P)#           S_left_val,S_left_ve  = Decomput_S(S_left,'descending')
#           S_right_val,S_right_ve  = Decomput_S(S_right,'ascending')#           # 计算投影矩阵W
#           self.W = Projection_W(S_left_ve,P)#      def nor_Z(self,x_train):
#           # 计算投影矩阵的特征矩阵Z
#           Z_train = Comput_Z(self.W,x_train,self.m)
#           norZ = log_Z(Z_train)#           return norZ#      def fit_nor_Z(self,x_train,y_train):
#           self.fit(x_train,y_train) #类内调用fit方法
#           fitnorZ = self.nor_Z(x_train) #类内调用nor_Z方法#           return fitnorZfrom sklearn import svm
if __name__ == '__main__':#设置训练测试数据+标签data = np.random.rand(10,512,32)x_train_l = datarandom.shuffle(data)x_train_r = datax_test = np.array([0])x_test = np.repeat(x_test,3)y_test = np.array([1])y_test = np.repeat(y_test,3)x_train = np.concatenate((x_train_l,x_train_r),axis=0)y_train = np.concatenate((x_test,y_test),axis=0)# X_train = torch.tensor(x_train)# Y_train = torch.tensor(y_train)model_acc = []model_std = []cov_left =  compute_cov(x_train_l)cov_right =  compute_cov(x_train_r)avg_cov = cov_left+cov_righteigval,eigve = Comput_Cov(avg_cov)P = White_Matrix(eigval,eigve)# 计算S矩阵+S的两个不同排列顺序的特征向量S_left = Comput_S(cov_left,P)S_right = Comput_S(cov_right,P)S_left_val,S_left_ve  = Decomput_S(S_left,'descending')S_right_val,S_right_ve  = Decomput_S(S_right,'ascending')# 计算投影矩阵WW = Projection_W(S_left_ve,P)# 计算投影矩阵的特征矩阵ZZ_train = Comput_Z(W,x_train)norZ = log_Z(Z_train)print(norZ.shape)#设置分类器model = svm()model_acc.append(cross_val_score(model, norZ, y_train).mean()*100)model_std.append(cross_val_score(model, x_train, y_train).std()*100)model.get_params()#画图fig, ax = plt.subplots(figsize=(7, 3))plt.rcParams.update({'font.size': 12})ax.set_title('Accuracy (%)')ax.bar(np.arange(1, 10), model_acc, color="#ffb152", yerr=model_std, capsize=3)ax.set(xticks=np.arange(1, 10), xlabel='Subject', yticks=np.arange(0, 101, step=10), ylabel='Accuracy',title='5-fold Cross Validation Result')ax.grid(axis='y', alpha=0.5)plt.savefig('5fold_train_result.jpg')plt.show()# csp = My_CSP()# clf =  make_pipeline([('CSP', csp), ('SVC', lda)])    # 创建机器学习的Pipeline,也就是分类模型，使用这种方式可以把特征提取和分类统一整合到了clf中# scores = cross_val_score(clf, x_train, y_train, cv=10) # 获取交叉验证模型的得分# My_CSP.fit(x_train,y_train)# lda.fit(x_train,y_train)# score_one = []# score_one.append(lda.score(x_train, y_train))# print(score_one)