二分以及练习题目-编程知识

二分模板

判断是否可以二分

（1）单调性

备选答案集是有序的

（2）二段性

在检查了mid是否符合要求之和，我可以舍弃左右某一边的答案

两个模板

关键词：满足条件的最小值，最大值最小，某个有序区间内某个数>=或者>key的第一个元素，或者当正确答案在左边时

while(l < r) {//check函数求当前值为mid情况下是否合法，如果合法，会想更小一点的值是不是合法的，所以会舍弃掉右边，去左边寻找更小的值，即r向左移动，因为mid是合法的，不能不要它，所以r=midif(check(mid)) {//满足要求，要求最小，再向左找看有没有更小的也满足要求r = mid;//因为mid也满足要求，所以要保留//如果不合法，只能扩大当前值，所以会舍弃掉左边，去右边寻找更大的值，即l向右移动，因为mid是不合法的，直接不要它，所以l=mid+1}else{l = mid + 1;//mid不满足要求，直接跳过就行}}

假设出现如下情况，l=l,r=l+1,此时mid=l。如果mid = (l+r)/2

（1）check(mid)返回为真，r = mid = l，正常退出

（2）check(mid)返回为假，l = r，正常退出

关键词：满足条件的最大值，最小值最大，某个有序区间内某个数<=或者<key的最后一个元素，或者当正确答案在左边时

while(l < r) {long mid = (l+r+1)/2;//注意这里要+1if(check(mid)) {//满足要求，要求最大，再向右找看有没有更大的也满足要求l = mid;//因为mid也满足要求，所以要保留}else{r = mid - 1;//mid不满足要求，直接跳过就行}}

假设出现如下情况，l=l,r=l+1,此时mid=l。如果mid = (l+r)/2

（1）check(mid)返回为真，l = mid = l，此时会陷入无限循环

（2）check(mid)返回为假，r < l，正常退出

假设出现如下情况，l=l,r=l+1,此时mid=l+1。如果mid = (l+r+1)/2

（1）check(mid)返回为真，l = mid = l+1=r，正常退出

（2）check(mid)返回为假，r = l，正常退出

分巧克力

题目分析

第一阶段二段性分析

希望巧克力的边长最大，而巧克力的边长要满足一个条件，就是按照该边长切出来的巧克力的块数应该大于等于K块才能满足K位小朋友都有巧克力。那么现在就是满足条件的最大值，我们要看一下他是否符合二段性，二分的关键在于二段性。

对于边长为mid的巧克力，如果它可以切出k块巧克力，那么我们可以确定边长小于mid的巧克力一定也可以，但是此时我需要找的是最大的边长，那么mid一定比小于mid的值更大，所以小于mid的值我就不用管了，也就是我可以确定我能够舍弃掉mid左边的值。我还想要确定比mid更大的边长是否也满足条件，所以我要在mid的右边继续二分。

if (check(mid)) {l = mid;} //因为mid是符合条件的，所以我要留着它，而不是l=mid+1

对于边长为mid的巧克力，如果它不可以切出k块巧克力，那么我们可以确定边长大于mid的巧克力一定也不可以，所以大于等于mid的值我就不用管了，也就是我可以确定我能够舍弃掉mid右边的值。我还想要寻找比mid更小的边长是否能满足条件，所以我要在mid的左边继续二分。

else { r = mid - 1; }//因为mid是不符合条件的，所以我不要留着它，而不是r=mid
//主要这里出现了减法，那么求mid那么应该是（l+r+1）/2

综上该题满足二段性，可以用二分，二分的板子就不说了，接下来说一下check函数如何写。

第二阶段写check函数

check(u)要实现的作用是检查边长为u的情况下能否切出k块巧克力。已知某块巧克力为 $W * H$ 大小，那么能够切出来的巧克力个数用 $(W / u) * (H / u)$ 表示。注意不能用 $(W * H) / (u * u)$ 表示。那么只需要遍历当前每一块巧克力，求出能个切割的巧克力总数和k比较就可以了，代码如下，

private static boolean check(int[][] a, int mid, int k) {int sum = 0;for (int i = 0; i < a.length; i++) {sum =sum + (a[i][0]/mid)*(a[i][1]/mid);}if(sum >= k) {return true;}return false;
}

第三步二分范围确定

那么这里的边长的最小值是1，最大值就是巧克力的最大边长，也就是100000。

题目代码

import java.util.Scanner;
public class Main {
public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int k = scanner.nextInt();int a[][] = new int[n][2];for (int i = 0; i < n; i++) {a[i][0] = scanner.nextInt();a[i][1] = scanner.nextInt();}int l = 1;int r = 100000;while(l<r) {int mid = (l + r + 1) / 2;if(check(a,mid,k)) {l = mid;}else {r = mid - 1;}}System.out.println(l);
}private static boolean check(int[][] a, int mid, int k) {int sum = 0;for (int i = 0; i < a.length; i++) {sum =sum + (a[i][0]/mid)*(a[i][1]/mid);}if(sum >= k) {return true;}return false;
}
}

#include <bits/stdc++.h>
using namespace std;
const int N=100010;
int n,k,u;
int h[N],w[N];
//check函数 检查是否能切k块巧克力
int m;//巧克力块数
bool check(int mid){m=0;for(int i=0;i<n;i++){m+=(w[i]/mid)*(h[i]/mid);}if(m>=k) return true;else return false;
}
int main(){cin>>n>>k;int l,r;l=1;r=1e5;for(int i=0;i<n;i++){cin>>h[i]>>w[i];}int mid;while(l<r){mid=(l+r+1)/2;if(check(mid)) l=mid;else r=mid-1;}cout<<l;return 0;
}

n,k=map(int,input().split())
a=[]
for i in range(n):x,y=map(int,input().split())a.append((x,y))
def check(m):n=0for x,y in a:n +=(x//m)*(y//m)return n>=k
left,right=1,100000
ans=1
while left<right:mid=(left+right+1)//2if check(mid):left=midelse:right=mid-1
print(left)

求阶乘

题目分析

第一阶段二分板子分析

我们要求满足N！末尾0的个数恰好为K的最小的N是不是就是求满足条件的最小，还是要考虑一下二分。

如果对于mid！末尾0的个数比K少，那么所有比mid小的值的阶乘包含的5的个数肯定更少，所以我可以把mid左边的值都舍弃掉，继续向mid右边寻找。

if(f(mid) < k ) {  l = mid + 1; }//此时mid是不符合条件的，我要舍弃它，所以l=mid+1，而不是mid

如果对于mid！末尾0的个数比K大，那么所有比mid大的值的阶乘包含的5的个数肯定更多，所以我可以把mid右边的值都舍弃掉，继续向mid左边寻找。

else { r = mid; }//此时mid是符合条件的，我要留着它，所以r=mid，而不是mid-1

综上满足二分的二段性，而check函数就是求解N！里面5的个数，接下来讲解。

第二阶段写check函数

如果直接去求，我们看一下，K的范围已经到了 $1^{18}$ ，这么大肯定有什么巧妙的地方，而不是直接求解。对于一个数字N而言，我们怎么去求他的阶乘末尾包含0的个数？末尾的0是如何产生的？是不是由 $2 * 5 = 10$ 产生的？我们只需要求N！里面包含几个2或者几个5就行了，那么由2或者5个数的最小值决定末尾0的个数，那么2和5而言，比如1-20里面，5，10，15，20包含5，而2，6，8，10，12，14，16，20里面包含2，也就是5的个数必然比2少，那么只需要求N！里面包含5的个数就可以了。那么这个求法大家可以记住，代码如下，

private static long f(long x) {long res = 0;while(x > 0) {res += x / 5;x = x / 5;}return res;
}

求x！里面包含5的个数，令x/5，直到x的值为0就停止。比如25里面5的个数等于sum+=25/5=sum+=5。25/5=5不等于0，所以还要再来一次sum+=5/5=sum+=1。此时就可以了。那么25里面包含6个5。其中5，10，15，20，都包含1个5，而25里面两个5，所以一共6个5。

第三阶段二分范围确定

这一道题，l=0，但是r应该如何确定呢？第一种方法直接一点，k=1e18，明显是long的范围，那么r我就初始化为long的最大值Long.MAX_VALUE是完全没有问题的。第二种方法，你要去求了，求一个精确的值，那么怎么求呢？我要求谁的阶乘末尾0的个数是1e18，你可以一个个试，

我试的过程如下图，最终得出了5e18就可以。

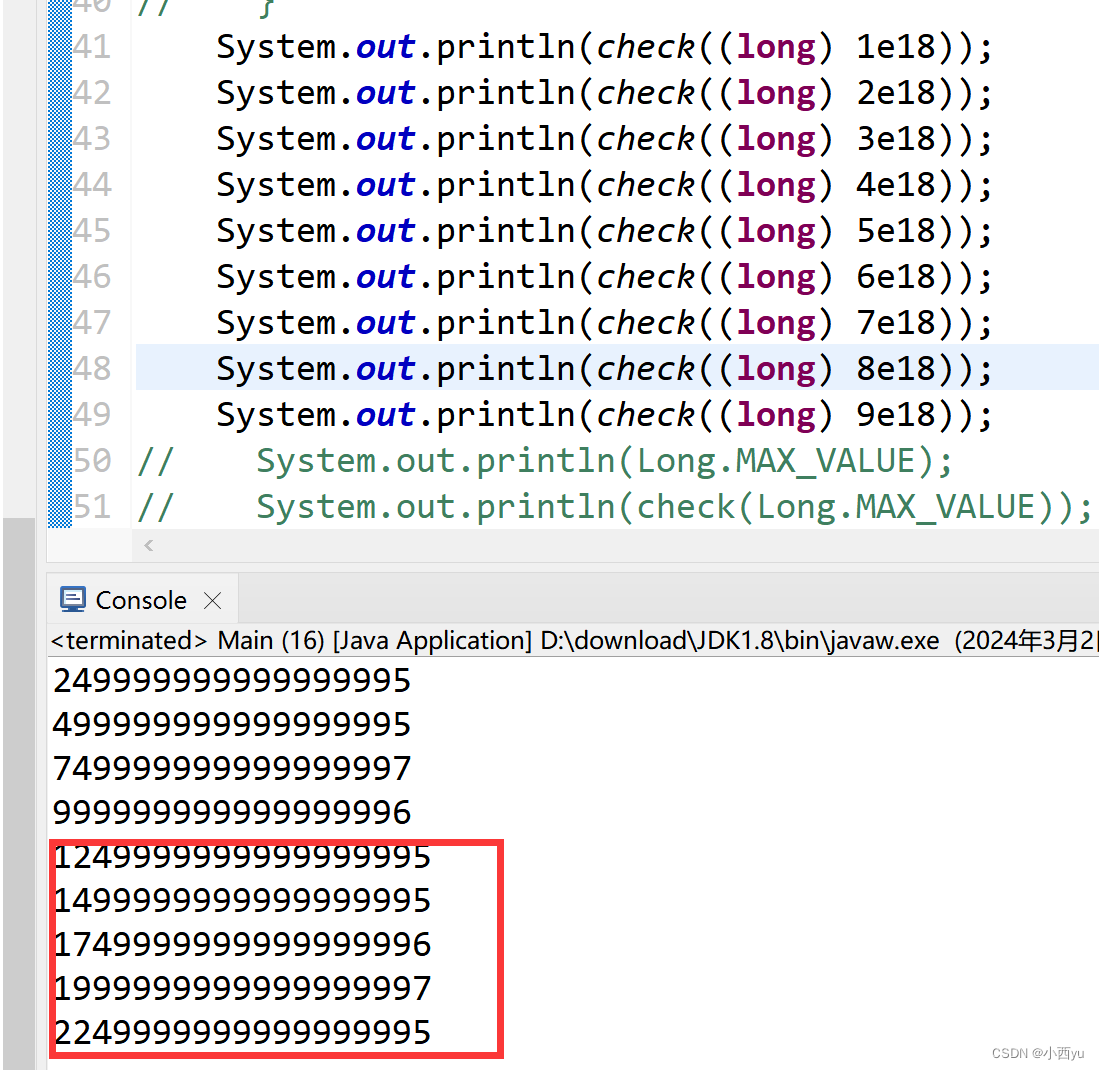
check函数是第二步介绍的，来求某个数的阶乘后面0的个数。

但是注意这里，我不能确定一定可以找到一个满足条件的解，对于分巧克力那道题，题目说了每个小朋友能够至少获得一块边长为1的巧克力，所以边长为1一定满足条件，一定有解。而本题也说了，这样的N可能不存在，所以在二分结束后，我要确定一下，当前的值是否满足条件。

题目代码

import java.util.Scanner;
public class Main {
public static void main(String[] args) {Scanner scanner = new Scanner(System.in);long k = scanner.nextLong();long l = 1,r = Long.MAX_VALUE-10;while(l < r) {long mid = (l+r)/2;if(f(mid) < k ) {l = mid + 1;}else {r = mid;}}if(f(l) == k) {System.out.println(l);}else {System.out.println(-1);}}private static long f(long x) {long res = 0;while(x > 0) {res += x / 5;x = x / 5;}return res;
}
}

卡牌

题目分析

想一下前面题的特点，是不是都出现了“最大边长”，“最小的数”这种字眼，那么这里出现了“最多能凑出多少套牌”，我们可以考虑用二分。接下来我们要看一下他是否符合二段性，二分的关键在于二段性。

第一阶段二段性分析

对于mid套牌，如果我们可以凑出来，那么我们可以确定套数小于mid的牌一定也可以，但是此时我需要找的是最多，那么mid一定比小于mid的值更大，所以小于mid的值我就不用管了，也就是我可以确定我能够舍弃掉mid左边的值。我还想要确定比mid更大的值是否也满足条件，所以我要在mid的右边继续二分。

if (check(mid)) {l = mid;} //因为mid是符合条件的，所以我要留着它，而不是l=mid+1

对于mid套牌，如果我们不可以凑出来，那么我们可以确定大于mid的套数一定也不可以，所以大于等于mid的值我就不用管了，也就是我可以确定我能够舍弃掉mid右边的值。我还想要寻找比mid更小的值是否能满足条件，所以我要在mid的左边继续二分。

else { r = mid - 1; }//因为mid是不符合条件的，所以我不要留着它，而不是r=mid
//主要这里出现了减法，那么求mid那么应该是（l+r+1）/2

综上该题满足二段性，可以用二分，二分的板子就不说了，接下来说一下check函数如何写。

第二阶段写check函数

check(u)要实现的作用是检查我能否凑出u套牌，也就是n种牌每一种的张数至少是n。我现在有m张空牌可以用，但是也有一个限制对于第i种牌，我手写的个数不能超过b[i]。整体思路是如果a[i]<u，我要手写u-a[i]张牌，如果u-a[i]>b[i]，然后我还要记录目前我手写的总牌数，超过m也是返回false。我可以返回false具体请看代码，

public static boolean check(int num) {//num为可以凑出来的卡牌组数long temp = m;//备份空白牌的数量for (int i = 0; i < a.length; i++) {//遍历卡牌if (a[i] >= num) continue;//如果卡牌数现在不满足至少为num张int add = num - a[i];//需要添加的扑克牌数量temp -= add;if (temp < 0) return false;//如果剩余的牌不够if (add > b[i]) return false;//如果超过预计需要画的牌个数}return true;}

第三阶段二分范围确定

l的值好确定，就是0，那么r呢？先来看一下a[i]的最大值是1e4，也就是每种牌我最多有4e5张，b[i]也是最多可以手写4e5张，那么加起来就是8e5，因此r可以取8e5+5。后面的5是随便加的数，一般要比你算出来的大一些就可以。

题目代码

import java.util.Scanner;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
public class Main {static int n;static long m;static int[] a, b;public static void main(String[] args) throws IOException {BufferedReader br = new BufferedReader(new InputStreamReader(System.in));String line = br.readLine();n = Integer.parseInt(line.split(" ")[0]);m = Long.parseLong(line.split(" ")[1]);//空白牌的数量a = new int[n];b = new int[n];int l = 0, r = 800005;String[] s = br.readLine().split(" ");for (int i = 0; i < n; i++) {a[i] = Integer.parseInt(s[i]);}s = br.readLine().split(" ");for (int i = 0; i < n; i++) {b[i] = Integer.parseInt(s[i]);}while (l < r) {//获取最大值int mid = (l + r + 1) / 2;if (check(mid)) {l = mid;} else {r = mid - 1;}}System.out.println(l);}public static boolean check(int num) {//num为可以凑出来的卡牌组数long temp = m;//备份空白牌的数量for (int i = 0; i < a.length; i++) {//遍历卡牌if (a[i] >= num) continue;//如果卡牌数现在不满足int add = num - a[i];//需要添加的扑克牌数量temp -= add;if (temp < 0) return false;//如果剩余的牌不够if (add > b[i]) return false;//如果超过预计需要画的牌个数}return true;}
}

#include <stdio.h>
#include <stdbool.h>
#define N 1000010int n;
long long m;
int a[N], b[N];bool check(int x){long long s = 0;for (int i = 0; i < n; i ++){if (a[i] >= x)continue;if (x - a[i] <= b[i])s += x - a[i];else return false;}if (s <= m)return true;return false;
}
int main(){scanf("%d%lld", &n, &m);for (int i = 0; i < n; i ++){scanf("%d", &a[i]);}for (int i = 0; i < n; i ++){scanf("%d", &b[i]);}int l = 0;int r = 8e8;while (l < r){int mid = (l + r + 1) / 2;if (check(mid)){l = mid;}elser = mid - 1;}printf("%d",l);return 0;
}

美丽的区间

题目分析

读题发现了一个关键字，“区间长度最短”，考虑用二分。对于一个长度为mid的区间，如果它的左右端点都不固定，其实我们不知道这个区间是哪个，因为长度为2的区间，可以是区间[1,2]也可以是区间[2,3]。所以我们固定区间端点，那么此时我们枚举左边界i，左边界二分去找，那么此时的mid表示的是区间右边界。如果mid往右走变大，区间长度会增大，如果mid往左走变小，区间长度会变小。区间长度为mid-i+1。

第一阶段二段性分析

对于长度为mid-i+1的区间，如果我们可以找到它的区间和大于等于S，那么我们可以确定右边界大于mid的区间一定也可以，因为区间里的值都是正数。但是此时我需要找的是最短，那么mid一定比大于mid的值更小，所以大于mid的值我就不用管了，也就是我可以确定我能够舍弃掉mid右边的值。我还想要确定比mid更小的值是否也满足条件，所以我要在mid的左边继续二分。

if(sum[mid] - sum[i-1] >= s) { r = mid;}//因为mid是符合条件的，所以我要留着它，而不是r=mid-1

对于长度为mid-i+1的区间，如果我们不可以找到它的区间和大于等于S，那么我们可以确定右边界小于mid的区间一定也不可以，因为区间里的值都是正数。所以小于mid的值我就不用管了，也就是我可以确定我能够舍弃掉mid左边的值。我还想要找比mid更大的值是否可以满足条件，所以我要在mid的右边继续二分。

else {l = mid + 1;}//因为mid是不符合条件的，所以我不要留着它，而不是l=mid

综上该题满足二段性，可以用二分，二分的板子就不说了，接下来说一下check函数如何写。

第二阶段写check函数

check(u)要实现的作用是检查区间和是否大于等于S，而求区间和最快的方式是利用前缀和求。

for (int i = 1; i < a.length; i++) {a[i] = scanner.nextInt();sum[i] = sum[i-1] + a[i];}
.......
if(sum[mid] - sum[i-1] >= s) {r = mid;
}else {l = mid + 1;
}

第三阶段二分范围确定

mid表示的是右边界，当左边界为i时，右边节最小去i，最大取n。

每次二分结束，我都要确定一下当前得到的l是否满足条件。最后输出的时候还是要确定一下我是否找到了满足条件的区间，因为这样的区间可能不存在。
mid表示的是右边界，当左边界为i时，右边节最小去i，最大取n。

每次二分结束，我都要确定一下当前得到的l是否满足条件。最后输出的时候还是要确定一下我是否找到了满足条件的区间，因为这样的区间可能不存在。

解释一下下面的代码，

if(sum[r] - sum[i-1] >= s) {ans = Math.min(ans, r-i+1);    }

为什么会有它呢？我们要知道二分求出来的l是什么，我们求出来的l是在区间左端点固定为i的情况下的一个答案，我们有多个左端点，也意味着我们有多个答案，那么我们求最短区间，就在这多个答案里求一个最小值就可以了，那么如何来表示答案呢。还是要注意我们二分求出来的l是左端点为i的情况下的右端点，那么我们的答案是区间长度，怎么表示呢？就是r-i+1，就是区间[i,l]的长度，因为这里是二分，l和r其实是相等的，写成r刚好和右端点对应，所以这里是r-i+1。

题目代码

import java.util.Scanner;
public class Main {
public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();long s = scanner.nextLong();int a[] = new int[n+1];long sum[] = new long[n+1];for (int i = 1; i < a.length; i++) {a[i] = scanner.nextInt();sum[i] = sum[i-1] + a[i];}long ans = Integer.MAX_VALUE;for (int i = 1; i < n + 1; i++) {//枚举右边界int l = i,r = n;while(l < r) {int mid = (l + r)/2;if(sum[mid] - sum[i-1] >= s) {r = mid;}else {l = mid + 1;}}if(sum[r] - sum[i-1] >= s) {ans = Math.min(ans, r-i+1);    }}if(ans == Integer.MAX_VALUE) {System.out.println(0);}else {System.out.println(ans);}
}
}

123

二分+等差数列求和+前缀和数组

题目分析

连续一段的和我们想到了前缀和，但是这里的l和r的范围为1e12，明显不能用O(n)的时间复杂度去求前缀和。那么我们开始观察序列的特点，可以按照等差数列对序列进行分块。如上图，在求前10个数的和的时候，我们可以这样求1+3（1+2）+6（1+2+3）+10（1+2+3+4）=20。我们不需要遍历10次就可以求出来。求前缀和代码如下

sum = new long[1500010];
for (int i = 1; i <= 1500000; i++) {t += i;sum[i] = sum[i-1]+t;
}

这里的t最开始等于1，是第一块的数字和，然后等于3，是第二块数字的和，然后等于6是第三块数字的和，以此类推。sum[i]表示的是分块后前i块包含数字的和。

我们可以求出前n块数字的和，那么我们需要知道第l个数字是在哪一块里面，然后求第l个数字是所在块的第几个数字。因为对于最后一块来说，不是所有的数字都会被包含进来，我们要单独对最后一块求数字和。

第一阶段利用二分求第x个数所在的块

图1

如图1所示，我们可以把这个序列分块，第一块有1个数，第二块有2个数，第三块有3个数，第四块有4个数，每一块拥有数的个数是一个等差数列。现在要找到序列中第x个数所在的块数，假设x=3，那么第x个数在第2块中，如果x=4，那么第x个数在第3块中。求第x个数所在的块数，就是求从左往右数，前缀和第一个大于等于x的块。

比如第2块的前缀和就是3，第三块的前缀和就是5。这个可以用二分去求。

    int l = 1;int r = 1500000;//最多可以分的块数while(l < r) {int mid = (l + r) / 2;if(sum(mid) < x) {//求mid个块中包含的数字的个数，如果小于x，就是不符合条件，我要向左找l = mid + 1;}else {//符合条件，我要看前面的块是否也是大于等于x的r = mid;}}

这里的sum函数的作用就是求前mid块中包含的数字的个数，因为是等差数列，所以直接用等差数列的求和公式就可以了，sum函数如下

private static long sum(long x) {    return (1L + x) * x / 2;
}

第二阶段求前x个数的前缀和

接下来分析二分结束之和我要怎么操作，我要求前x个数字的和。

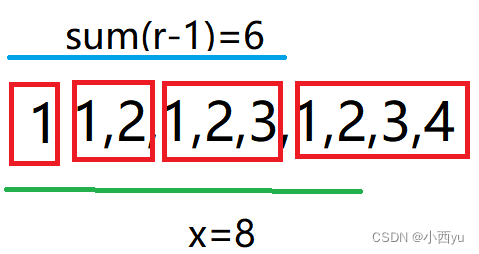
假设x=8，那么第x个数在第4块中，我还要知道，第x个数是第4块中的第几个数字。如图，第4块有4个数，第x个数第4块的第2个数上，那么第2个数是怎么来的呢？就是x-sum(r-1)=8-6=2。其实就是我二分算出来了第x个数在第r块上，那么我只需要把前r-1块包含的数的个数减去就算出来x是在第r块上的第几个数上了。结合上图更好理解。那么前x个数的和就是前r-1块包含数的和加上第r块里面前x-sum(r-1)个数的和。

某一块里面包含的数也是等差数列，求前n个数的和依然可以直接用sum(n)去求。而数组sum[r]里面记录的是前r块包含数字值的前缀和。所以二分结束后的代码是这样子的

private static long f(long x) {int l = 1;int r = 1500000;//最多可以分的块数while(l < r) {int mid = (l + r) / 2;if(sum(mid) < x) {//求mid个块中包含的数字的个数l = mid + 1;}else {r = mid;}}//r--是表示完整的块的个数r--;//就是上文里的r-1//x表示x处在他所在块的第几个位置，需要减去前面所有块包含的数的个数//本来要求x个数字，前r个块中已经包含了sum(r)个数字，第r+1个块x -= sum(r);//前r个块中已经包含了多少个数字return sum[r]+sum(x);
}

还是对于x=8的例子，二分求出来r=4，r–后，r=3，sum[3]=10。x-=sum(3)=8-6=2。sum[3]+sum(2)=10+3=13

注意这道题里对于sum函数的多次应用，但是不是每一次应用含义都是一样的。因为每一块包含的数字个数是等差数列，而每一块内每个数字形成的也是等差数列。

题目代码

import java.util.Scanner;
public class Main {
static long[] sum;
public static void main(String[] args) {Scanner scanner = new Scanner(System.in);long t = 0;//前缀和的预处理sum = new long[1500010];for (int i = 1; i <= 1500000; i++) {t += i;sum[i] = sum[i-1]+t;}int n = scanner.nextInt();while(n-- > 0) {long l = scanner.nextLong();long r = scanner.nextLong();System.out.println(f(r)-f(l-1));//f(r)求的是序列中前r个数的和}
}
//二分  二分求的是x在哪一块中 n*（n-1）/2>l的第一个n
private static long f(long x) {int l = 1;int r = 1500000;//最多可以分的块数while(l < r) {int mid = (l + r) / 2;if(sum(mid) < x) {//求mid个块中包含的数字的个数l = mid + 1;}else {r = mid;}}//r--是表示完整的块的个数r--;//x表示x处在他所在块的第几个位置，需要减去前面所有块包含的数的个数//本来要求x个数字，前r个块中已经包含了sum(r)个数字，第r+1个块x -= sum(r);//前r个块中已经包含了多少个数字return sum[r]+sum(x);
}
//sum函数求前x块包含的数的个数，同时也可以表示某一个块中，前x个数的总和
private static long sum(long x) {// TODO Auto-generated method stub    return (1L + x) * x / 2;
}
}

晾衣服

二分

题目分析

这里出现了“最小化干燥的总时间”，那么可以考虑用二分去做。

第一阶段二段性分析

假设当前需要耗费的时间为mid分钟，如果mid分钟内可以烘干这些衣服，那么我们可以确定右边界大于mid的区间一定也可以。但是此时我需要找的是最短时间，那么mid一定比大于mid的值更小，所以大于mid的值我就不用管了，也就是我可以确定我能够舍弃掉mid右边的值。我还想要确定比mid更小的值是否也满足条件，所以我要在mid的左边继续二分。

if(check(mid)) {r = mid;}//因为mid是符合条件的，所以我要留着它，而不是r=mid-1

假设当前需要耗费的时间为mid分钟，如果mid分钟内不可以烘干这些衣服，那么我们可以确定右边界小于mid的区间一定也不可以。所以小于mid的值我就不用管了，也就是我可以确定我能够舍弃掉mid左边的值。我还想要找比mid更大的值是否可以满足条件，所以我要在mid的右边继续二分。

else {l = mid + 1;}//因为mid是不符合条件的，所以我不要留着它，而不是l=mid

综上该题满足二段性，可以用二分，二分的板子就不说了，接下来说一下check函数如何写。

第二阶段写check函数

check(u)要实现的作用是检查能否在mid分钟内烘干这些衣服。对于一个衣服的湿度a[i]，如果他大于mid，就需要使用烘干机，使用的时间是(a[i]-mid)/(k-1)。因为烘干衣服不足1分钟也要按一分钟算，所以这里要上取整。

这里为什么是k-1呢？我们要保证在mid分钟内烘干，因为衣服每一分钟湿度都会减1，如果我把衣服放在烘干机上湿度会减k，那么放在烘干机和不放在烘干机上会比原来多减了k-1。我们要注意的是，烘干机使用的总时间不能超过mid。

假设我只有一个衣服需要烘干，如果mid=3，a[i]=10，k=3。a[i]-mid=10-3=7。如果是7/3=3。这样看mid等于3是可以的，但是我把烘干机全用在这一个衣服上所需要的烘干时间是10/3=4>mid=3，明确不可以在3分钟内烘干该衣服。所以我这里应该是7/2=4，此时可以判断出来不可以在3分钟内烘干该衣服。check函数如下，

static boolean check(int mid) {long s = 0;for (int i = 0; i < n; i++) {if (a[i] > mid) {s += (long)(a[i] - mid + k - 2) / (k - 1);}}return s <= mid;}

第三阶段二分范围确定

烘干的时间最长就是不使用烘干机，自然风干需要a[i]分钟，而a[i]最大是1e9，所以l=0，r=1e9。

注意一个特殊情况，如果k=1，那么其实烘干机有和没有都一样，自然风干所需要的时间就是所有衣服中最大的湿度。

for (int i = 0; i < n; i++) {a[i] = sc.nextInt();maxV = Math.max(maxV, a[i]);
}
k = sc.nextInt();
if (k == 1) {System.out.println(maxV);return;
}

题目代码

import java.util.Scanner;
public class Main {static int N = 100010;static int n, k;static int[] a = new int[N];public static void main(String[] args) {Scanner sc = new Scanner(System.in);n = sc.nextInt();int maxV = 0;for (int i = 0; i < n; i++) {a[i] = sc.nextInt();maxV = Math.max(maxV, a[i]);}k = sc.nextInt();if (k == 1) {System.out.println(maxV);return;}int l = 1, r = (int) 1e9;int res = 0;while (l < r) {int mid = (l + r)/2;if (check(mid)) {r = mid;} else {l = mid + 1;}}System.out.println(l);}static boolean check(int mid) {long s = 0;for (int i = 0; i < n; i++) {if (a[i] > mid) {s += Math.ceil((a[i]-mid)*1.0 / (k - 1));}}return s <= mid;}
}

妮妮的月饼工厂

题目分析

这里出现了“最高高度”，那么可以考虑用二分去做。

第一阶段二段性分析

希望月饼的高度最大，而月饼的高度要满足一个条件，就是按照该高度切出来的月饼的块数应该大于等于K块。那么现在就是满足条件的最大值，我们要看一下他是否符合二段性，二分的关键在于二段性。

对于高度为mid的月饼，如果它可以切出k块月饼，那么我们可以确定高度小于mid的月饼一定也可以，但是此时我需要找的是最大的高度，那么mid一定比小于mid的值更大，所以小于mid的值我就不用管了，也就是我可以确定我能够舍弃掉mid左边的值。我还想要确定比mid更大的高度是否也满足条件，所以我要在mid的右边继续二分。

if (check(mid)) {l = mid;} //因为mid是符合条件的，所以我要留着它，而不是l=mid+1

对于高度为mid的月饼，如果它不可以切出k块月饼，那么我们可以确定边长大于mid的月饼一定也不可以，所以大于等于mid的值我就不用管了，也就是我可以确定我能够舍弃掉mid右边的值。我还想要寻找比mid更小的月饼是否能满足条件，所以我要在mid的左边继续二分。

else { r = mid - 1; }//因为mid是不符合条件的，所以我不要留着它，而不是r=mid
//主要这里出现了减法，那么求mid那么应该是（l+r+1）/2

综上该题满足二段性，可以用二分，二分的板子就不说了，接下来说一下check函数如何写。

第二阶段写check函数

check(u)要实现的作用是检查高度为u的情况下能否切出k块月饼。已知某个月饼高度为 $H$ 大小，那么能够切出来的月饼个数用 $(H / u)$ 表示。那么只需要遍历当前每一块月饼，求出能个切割的月饼总数和k比较就可以了，代码如下，

private static boolean check(int u) {long res = 0l;for(int i = 1;i <=n;i++) {res += a[i]/u;}if(res >= k) return true;return false;
}

第三步二分范围确定

那么这里的高度的最小值是1，最大值就是月饼的最大边长，也就是1e9。注意本题没有说一定能找到符合条件的高度，所以最后输出的时候要判断一下。

题目代码

import java.util.Scanner;
public class Main {static long a[];static int n;static long k;
public static void main(String[] args) {Scanner scanner = new Scanner(System.in);n = scanner.nextInt();k = scanner.nextLong();a = new long[n+1];for(int i = 1;i<=n;i++) {a[i]=scanner.nextInt();}int l = 1,r = (int) 1e9;while(l < r) {int mid = (l+r+1)/2;if(check(mid)) l = mid;else r = mid-1;}if(!check(l)) System.out.println(-1);//忘了这个判断else System.out.println(l);
}
private static boolean check(int u) {// TODO Auto-generated method stublong res = 0l;for(int i = 1;i <=n;i++) {res += a[i]/u;}if(res >= k) return true;return false;
}
}