一、基变换

成为一组基的唯一要求是：线性无关（非正交基也可以，但由于正交基有较好的性质，所以通常使用正交基。）

基变换的矩阵表示： 一般地，如果我们有M个N维向量，想将其变换为由R个N维向量表示的新空间中，那么首先将R个新基按行组成矩阵A，然后将向量按列组成矩阵B，那么两矩阵的乘积AB就是基变换的结果，其中AB的第m列为B中第m列变换后的结果，数学表示为：
$$\left(\begin{array}{c}{p}_1\\ p_2\\ .\\ .\\ .\\ p_R\end{array}\right)\left(\begin{array}{cccc}{a}_1& a_2& ...& a_M\end{array}\right)=\left(\begin{array}{cccc}{p}_1{a}_1& p_1{a}_2& \cdots & p_1{a}_M\\ p_2{a}_1& p_2{a}_2& \cdots & p_2{a}_M\\ ⋮& ⋮& \ddots & ⋮\\ p_N{a}_1& p_N{a}_2& \cdots & p_N{a}_M\end{array}\right)$$
其中，R决定了基变换后的数据维度，且R可以小于M，当R<M时就是数据降维。

由此可以给出矩阵相乘的另一种物理解释：两个矩阵相乘的意义是将右边矩阵中的每一列列向量变换到以左边矩阵中每一行行向量为基的空间中去。

PCA本质就是一种换底操作，将原来的数据集换到另一组基向量坐标体系下后，这组数据能够用更小的数据量达到较大的代表性的效果。

二、数据降维

2.1 为什么要进行数据降维？

（1）算法复杂度呈指数级关联，当数据维度过大时，会消耗过多的计算机资源；

（2）各维数据间常常存在相关性，可以在保证算法性能的前提下，通过合理的降维方法将信息的损失降到最低。

2.2 优化目标

协方差矩阵：包含了各维度自身的方差信息，也包含了各维度间的协方差信息（即相关性信息），因此计算协方差矩阵是数据降维过程中的重要步骤。

欲将一组N维向量降到K维（0<K<N），其目标是选择K个单位正交基，使得原始数据变换到这组基上，各维度间协方差为0，而各维度自身的方差尽可能大，并且最终只取最大的K个方差。

最大特征值对应的特征向量就是点向量平方和最大的方向，等价于方差最大的方向（变换之后保留尽可能多的信息，如果方差很小表明数据不能很好的区分开，就会有信息损失）。 因此优化目标就是找协方差矩阵的最大的K个特征值和特征向量，这K个特征向量按对应特征值从大到小按行排列就组成了数据降维用到的变换矩阵P，Y=PX就是降维后的数据矩阵。

协方差矩阵特征值的几何意义

PCA算法详解——本质上就是投影后使得数据尽可能分散（方差最大）

三、PCA算法步骤

设原始数据集有M条N维数据，欲将其降维到K维，则PCA降维算法步骤如下：

（1）将原始数据按列组成N×M的矩阵X；

（2）求矩阵X的协方差矩阵C；

（3）求矩阵C的特征值及对应的特征向量；

（4）取其中K个最大的特征值并从大到小按排列，并将其对应的特征向量按行排列成矩阵P；

（5）Y=PX即为降维后的数据集（按列排列了，矩阵大小为K×M）。

CodingLabs - PCA的数学原理

四、求解特征值、特征向量

可以看出，PCA算法问题的关键在于特征值和特征向量的计算，该问题常用协方差矩阵的分解来解决。常用的两种矩阵分解方法是特征值分解（仅适用于方阵）、奇异值分解（任何矩阵都适用），因此这也是PCA算法的两种实现方法。

4.1 特征值分解（ED）

$$C=Q\Sigma Q^{-1}$$

其中，$Q$是矩阵$C$的特征向量组成的矩阵，$\Sigma$是一个对角阵，对角线上的元素是对应的特征值。

4.2 奇异值分解（SVD）

$$C=U\Sigma V^T$$

其中：

• $C{C}^T$的归一化的特征向量构成左奇异矩阵$U$；
• $C^{T}C$的归一化的特征向量构成右奇异矩阵$V$；
• $C{C}^T$或$C^{T}C$的特征值的平方根构成对角阵$\Sigma$。

主成分分析（PCA）原理详解

机器学习中SVD总结

《三维点云处理》学习笔记（1）：平面法向量估计

五、Kernel PCA

PCA是线性方法，因为矩阵乘以一个向量，只是对矩阵列的重新线性组合。

$\varphi$是升维函数。

六、Python代码

6.1 读取数据

import os
from pyntcloud import PyntCloud
import open3d as o3d
import numpy as npdef main():root_dir = r"..\modelnet40_normal_resampled\modelnet40_normal_resampled"shapenames = "modelnet40_shape_names.txt"with open (os.path.join(root_dir, shapenames)) as f:shape_name_list = f.readlines()  # .readlines一次性读取所有数据，按行存成listfor item in shape_name_list:name = item.strip()file_path_name = os.path.join(root_dir, name) + r"\\{}_0001.txt".format(name)  # 只读取每个类别的第一个点云数据point_cloud_pynt = PyntCloud.from_file(file_path_name, sep=",", names=["x", "y", "z", "nx", "ny", "nz"])point_cloud_o3d = point_cloud_pynt.to_instance("open3d", mesh=False)  # 将数据转成open3d格式，不生成网格数据，只转为点云数据o3d.visualization.draw_geometries(([point_cloud_o3d]))  # 可视化原始点云数据points = point_cloud_pynt.points  # .points之后是DataFrame格式points_loc = np.array(points.loc[:, ["x", "y", "z"]])  # .loc通过指定列名称来索引# points_loc = np.array(points.iloc[:, [0, 1, 2]])  # .iloc通过指定列索引值来索引if __name__ == "__main__":main()

6.2 PCA实现

注意：使用矩阵相乘的形式计算协方差矩阵时，记得要除以[点数-1]！！！协方差矩阵计算方法

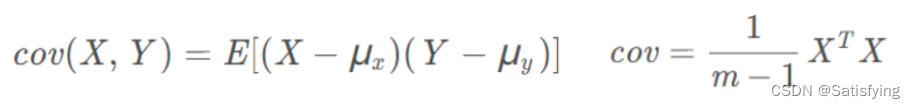
def PCA(data, k):data_new = np.array(data - data.mean(axis=0))  # 去中心化H = np.dot(data_new.T, data_new) / (data_new.shape[0] - 1)  # 计算协方差矩阵，矩阵相乘后除以[点数-1]# H = np.cov(data.T)  # 计算结果维度和输入数据行数保持一致，因此输入数据要进行转置（np.cov输入数据去不去中心化结果一样）# # 使用ED分解# eigen_vals, eigen_vecs = np.linalg.eig(H)# sort_index = np.argsort(eigen_vals)[::-1]# select_eigen_vecs = eigen_vecs[:, sort_index[:k]]# 使用SVD分解U, S, V = np.linalg.svd(H)sort_index = np.argsort(S)[::-1]  # np.argsort()返回排序后的索引顺序，这里按照降序排列select_eigen_vecs = U[:, sort_index[:k]]  # 求前k大的奇异值对应的特征向量# 计算PCA后的结果，并可视化points_after_PCA = np.dot(data_new, select_eigen_vecs)  # 要使用去中心化的数据进行运算！！！pcd = o3d.geometry.PointCloud()pcd.points = o3d.utility.Vector3dVector(points_after_PCA)o3d.visualization.draw_geometries([pcd])return select_eigen_vecsK = 3  # PCA降维目标维度
Vecs = PCA(points_loc, K)

6.3 运行结果

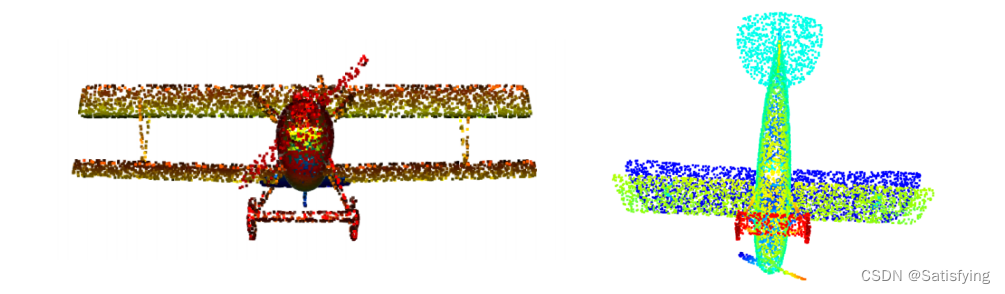
原始点云如下左图，PCA之后的点云如下右图：

七、结论

1. PCA本质是对数据进行基变换，通过选择方差最大的几个方向作为基向量的方向，变换之后数据会更具代表性。也就是说当PCA算法没有改变数据维度时，本质只是将点云变换到了更容易辨别出目标类别的方向上（即方差最大的几个方向）；
2. PCA实现过程中不同的协方差矩阵计算方式（直接代入公式求解、调用库函数），对结果的影响只是影响处理之后数据的方向；
3. PCA实现过程中不同的矩阵分解方式（特征值分解ED、奇异值分解SVD），对结果的影响也只是方向不同。

 
（本⽂完整的pdf请关注公众号“张张学算法”，并回复“pdf”获取~）