文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 进阶
- 解法一
- 思路和算法
- 代码
- 复杂度分析
- 解法二
- 思路和算法
- 代码
- 复杂度分析
- 解法三
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:二叉搜索树迭代器
出处:173. 二叉搜索树迭代器
难度
4 级
题目描述
要求
实现 BSTIterator \texttt{BSTIterator} BSTIterator 类,表示一个按中序遍历二叉搜索树的迭代器:
- BSTIterator(TreeNode root) \texttt{BSTIterator(TreeNode root)} BSTIterator(TreeNode root) 初始化 BSTIterator \texttt{BSTIterator} BSTIterator 类的一个对象。二叉搜索树的根结点 root \texttt{root} root 会作为构造函数的一部分给出。指针应初始化为一个不存在于二叉搜索树中且小于二叉搜索树中的任何元素的数字。
- boolean hasNext() \texttt{boolean hasNext()} boolean hasNext() 如果向指针右侧遍历存在数字,则返回 true \texttt{true} true,否则返回 false \texttt{false} false。
- int next() \texttt{int next()} int next() 将指针向右移动,然后返回指针处的数字。
注意,指针初始化为一个不存在于二叉搜索树中的数字,所以对 next() \texttt{next()} next() 的首次调用将返回二叉搜索树中的最小元素。
你可以假设 next() \texttt{next()} next() 调用总是有效的,也就是说,当调用 next() \texttt{next()} next() 时,中序遍历中至少存在一个下一个数字。
示例
示例 1:
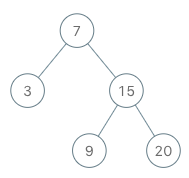
输入:
["BSTIterator", "next", "next", "hasNext", "next", "hasNext", "next", "hasNext", "next", "hasNext"] \texttt{["BSTIterator", "next", "next", "hasNext", "next", "hasNext", "next", "hasNext", "next", "hasNext"]} ["BSTIterator", "next", "next", "hasNext", "next", "hasNext", "next", "hasNext", "next", "hasNext"]
[[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []] \texttt{[[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []]} [[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []]
输出:
[null, 3, 7, true, 9, true, 15, true, 20, false] \texttt{[null, 3, 7, true, 9, true, 15, true, 20, false]} [null, 3, 7, true, 9, true, 15, true, 20, false]
解释:
BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]); \texttt{BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]);} BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]);
bSTIterator.next(); \texttt{bSTIterator.next();} bSTIterator.next(); // 返回 3 \texttt{3} 3
bSTIterator.next(); \texttt{bSTIterator.next();} bSTIterator.next(); // 返回 7 \texttt{7} 7
bSTIterator.hasNext(); \texttt{bSTIterator.hasNext();} bSTIterator.hasNext(); // 返回 True \texttt{True} True
bSTIterator.next(); \texttt{bSTIterator.next();} bSTIterator.next(); // 返回 9 \texttt{9} 9
bSTIterator.hasNext(); \texttt{bSTIterator.hasNext();} bSTIterator.hasNext(); // 返回 True \texttt{True} True
bSTIterator.next(); \texttt{bSTIterator.next();} bSTIterator.next(); // 返回 15 \texttt{15} 15
bSTIterator.hasNext(); \texttt{bSTIterator.hasNext();} bSTIterator.hasNext(); // 返回 True \texttt{True} True
bSTIterator.next(); \texttt{bSTIterator.next();} bSTIterator.next(); // 返回 20 \texttt{20} 20
bSTIterator.hasNext(); \texttt{bSTIterator.hasNext();} bSTIterator.hasNext(); // 返回 False \texttt{False} False
数据范围
- 树中结点数目在范围 [1, 10 5 ] \texttt{[1, 10}^\texttt{5}\texttt{]} [1, 105] 内
- 0 ≤ Node.val ≤ 10 6 \texttt{0} \le \texttt{Node.val} \le \texttt{10}^\texttt{6} 0≤Node.val≤106
- 最多调用 10 5 \texttt{10}^\texttt{5} 105 次 hasNext \texttt{hasNext} hasNext 和 next \texttt{next} next 操作
进阶
你是否可以将 hasNext() \texttt{hasNext()} hasNext() 和 next() \texttt{next()} next() 实现为平均时间复杂度 O(1) \texttt{O(1)} O(1) 并使用 O(h) \texttt{O(h)} O(h) 内存,其中 h \texttt{h} h 是树的高度?
解法一
思路和算法
只要得到二叉搜索树的中序遍历序列,并维护指针指向的下标,即可实现二叉搜索树迭代器。
构造方法中,对给定的二叉搜索树中序遍历,使用列表存储中序遍历的结果,并将指针初始化为指向下标 − 1 -1 −1。指针指向的下标为上一个遍历的数字下标, − 1 -1 −1 表示尚未遍历任何数字。
对于 hasNext \textit{hasNext} hasNext 操作,需要判断向指针右侧遍历是否存在数字,等价于判断指针指向的下标右侧是否存在数字,因此当指针指向的下标右侧存在数字时返回 true \text{true} true,否则返回 false \text{false} false。
对于 next \textit{next} next 操作,将指针向右移动等价于将指针指向的下标加 1 1 1,在更新指针指向的下标之后,返回该下标处的数字。
二叉搜索树的中序遍历可以通过递归、迭代或者莫里斯遍历实现,其中递归实现和迭代实现都需要栈空间,莫里斯遍历使用常数空间,但是由于需要存储中序遍历序列,因此对于结点数为 n n n 的二叉搜索树,都需要 O ( n ) O(n) O(n) 的空间存储中序遍历序列。
代码
下面的代码为递归实现二叉搜索树中序遍历的做法。
class BSTIterator {private List<Integer> traversal;private int index;public BSTIterator(TreeNode root) {traversal = new ArrayList<Integer>();inorder(root);index = -1;}public boolean hasNext() {return index + 1 < traversal.size();}public int next() {return traversal.get(++index);}private void inorder(TreeNode node) {if (node == null) {return;}inorder(node.left);traversal.add(node.val);inorder(node.right);}
}
下面的代码为迭代实现二叉搜索树中序遍历的做法。
class BSTIterator {private List<Integer> traversal;private int index;public BSTIterator(TreeNode root) {traversal = new ArrayList<Integer>();Deque<TreeNode> stack = new ArrayDeque<TreeNode>();TreeNode node = root;while (!stack.isEmpty() || node != null) {while (node != null) {stack.push(node);node = node.left;}node = stack.pop();traversal.add(node.val);node = node.right;}index = -1;}public boolean hasNext() {return index + 1 < traversal.size();}public int next() {return traversal.get(++index);}
}
下面的代码为莫里斯遍历实现二叉搜索树中序遍历的做法。
class BSTIterator {private List<Integer> traversal;private int index;public BSTIterator(TreeNode root) {traversal = new ArrayList<Integer>();TreeNode node = root;while (node != null) {if (node.left == null) {traversal.add(node.val);node = node.right;} else {TreeNode predecessor = node.left;while (predecessor.right != null && predecessor.right != node) {predecessor = predecessor.right;}if (predecessor.right == null) {predecessor.right = node;node = node.left;} else {predecessor.right = null;traversal.add(node.val);node = node.right;}}}index = -1;}public boolean hasNext() {return index + 1 < traversal.size();}public int next() {return traversal.get(++index);}
}
复杂度分析
-
时间复杂度:构造方法的时间复杂度是 O ( n ) O(n) O(n),方法 hasNext \textit{hasNext} hasNext 和方法 next \textit{next} next 的时间复杂度都是 O ( 1 ) O(1) O(1),其中 n n n 是二叉搜索树的结点数。构造方法需要 O ( n ) O(n) O(n) 的时间对二叉搜索树中序遍历,方法 hasNext \textit{hasNext} hasNext 和方法 next \textit{next} next 根据下标值得到结果,时间都是 O ( 1 ) O(1) O(1)。
-
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉搜索树的结点数。存储中序遍历序列需要 O ( n ) O(n) O(n) 的空间。
解法二
思路和算法
解法一需要存储完整的中序遍历序列,因此空间复杂度与结点数相关。利用中序遍历的迭代实现,可以将空间复杂度降低到与二叉搜索树的高度相关,虽然最坏情况下二叉搜索树的高度等于结点数,但是平均情况下二叉搜索树的高度小于结点数,因此空间复杂度更低。
为了不存储完整的中序遍历序列,不能在构造方法中完成中序遍历,而是应该在 next \textit{next} next 操作中完成中序遍历,每次调用 next \textit{next} next 操作时访问一个结点。因此,需要维护用于迭代实现中序遍历的栈以及当前结点,在构造方法中将栈初始化,并将当前结点初始化为二叉搜索树的根结点。
对于 hasNext \textit{hasNext} hasNext 操作,如果栈不为空或者当前结点不为空则返回 true \text{true} true,否则返回 false \text{false} false。
对于 next \textit{next} next 操作,模拟中序遍历的迭代实现的操作,访问一个结点。
代码
class BSTIterator {private Deque<TreeNode> stack;private TreeNode node;public BSTIterator(TreeNode root) {stack = new ArrayDeque<TreeNode>();node = root;}public boolean hasNext() {return !stack.isEmpty() || node != null;}public int next() {while (node != null) {stack.push(node);node = node.left;}node = stack.pop();int val = node.val;node = node.right;return val;}
}
复杂度分析
-
时间复杂度:构造方法的时间复杂度是 O ( 1 ) O(1) O(1),方法 hasNext \textit{hasNext} hasNext 的时间复杂度是 O ( 1 ) O(1) O(1),方法 next \textit{next} next 的均摊时间复杂度是 O ( 1 ) O(1) O(1)。构造方法初始化栈和当前结点的时间是 O ( 1 ) O(1) O(1),方法 hasNext \textit{hasNext} hasNext 判断栈是否为空和当前结点是否为空的时间是 O ( 1 ) O(1) O(1),方法 next \textit{next} next 的调用过程中会访问每个结点一次且每个结点入栈和出栈各一次,因此均摊时间复杂度是 O ( 1 ) O(1) O(1)。
-
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉搜索树的结点数。空间复杂度主要是栈空间,取决于二叉搜索树的高度,最坏情况下二叉搜索树的高度是 O ( n ) O(n) O(n)。
解法三
思路和算法
解法二不是在构造方法中完成中序遍历,而是在 next \textit{next} next 操作中完成中序遍历,避免了存储中序遍历序列,但是由于使用迭代实现中序遍历,仍需要使用栈空间。为了将空间复杂度降低到 O ( 1 ) O(1) O(1),需要使用莫里斯遍历实现中序遍历,在 next \textit{next} next 操作中完成中序遍历。
需要维护用于莫里斯遍历实现中序遍历的当前结点,在构造方法中将当前结点初始化为二叉搜索树的根结点。
对于 hasNext \textit{hasNext} hasNext 操作,如果当前结点不为空则返回 true \text{true} true,否则返回 false \text{false} false。
对于 next \textit{next} next 操作,模拟中序遍历的莫里斯遍历实现的操作,访问一个结点。
代码
class BSTIterator {private TreeNode node;public BSTIterator(TreeNode root) {node = root;}public boolean hasNext() {return node != null;}public int next() {int val = -1;while (val < 0) {if (node.left == null) {val = node.val;node = node.right;} else {TreeNode predecessor = node.left;while (predecessor.right != null && predecessor.right != node) {predecessor = predecessor.right;}if (predecessor.right == null) {predecessor.right = node;node = node.left;} else {predecessor.right = null;val = node.val;node = node.right;}}}return val;}
}
复杂度分析
-
时间复杂度:构造方法的时间复杂度是 O ( 1 ) O(1) O(1),方法 hasNext \textit{hasNext} hasNext 的时间复杂度是 O ( 1 ) O(1) O(1),方法 next \textit{next} next 的均摊时间复杂度是 O ( 1 ) O(1) O(1)。构造方法初始化当前结点的时间是 O ( 1 ) O(1) O(1),方法 hasNext \textit{hasNext} hasNext 判断当前结点是否为空的时间是 O ( 1 ) O(1) O(1),方法 next \textit{next} next 的调用过程中会访问每个结点两次,因此均摊时间复杂度是 O ( 1 ) O(1) O(1)。
-
空间复杂度: O ( 1 ) O(1) O(1)。