Chap 3. Feature Indexing and Retrieval

什么是索引？
为了提高数据集的检索效率而生成的结构化信息

基于特征的相似度匹配是多媒体数据检索方法的基础
从多媒体对象中提取重要特征，将其转化成高维特征向量存储在数据库中

相似性度量：
两种查询任务：

相似性查询可以通过扫描数据库来实现，但代价非常高
过滤 精简模式： Filter & Refine
近似策略快速过滤，对筛选后的结果精确比较
过滤策略需要满足两个条件：
候选集不能丢失任何可能的对象（ 保证召回率
候选集包含的对象不能比真实相关对象多太多（ 保证精度

核心问题 ：如何高效的基于特征向量计算多媒体对象之间的相似性或距离？
特征向量通常是高维的三维空间中的点、立方体、球
文本、音频、图像等多媒体特征数据
常用的线性匹配查询，在高维特征条件下速度非常慢，需要研究特殊的技术和数据结构来支持高效的相似性匹配
高维数据的特点：
具有复杂的结构：可能是一个点，也可能是更复杂的图形，难以对高维数据排序
思路 ：特征空间结构化
有了结构才能进行高效的索引，每次查询只需要检索少数几个子空间
高维索引就是针对高维空间进行空间划分和检索的技术和数据结构
影响查询效率的关键因素是磁盘的 I/O 次数，利用索引技术可以有效减少 I/O 次数
树结构非常自然的适用于索引结构

多维索引法
R tree 及其变形、 kd tree 等
近似最近邻法
VA File 等
降维法
iDistance 等
基于聚类的索引方法
Clindex 等

▪ 基于B树的索引方法
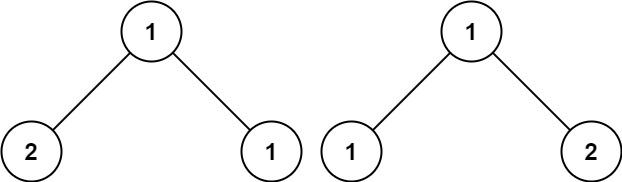
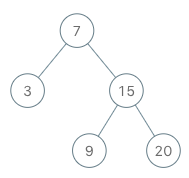
▪ B树，即二叉搜索树，其特点包括
▪ 1. 所有非叶子节点至多拥有两个子节点
▪ Left和Right
▪ 2. 所有的节点存储一个关键字
▪ 3. 非叶子节点的左指针指向小于其关键字的子
树，右节点指向大于其关键字的子树
▪ 数据的多维性使得传统的B树索引不再适合
▪ B树在一个维度上比较数据间的关系
▪ 大于、小于、等于
▪ 需要研究能适应高维特性的空间索引方式

▪ R-tree
▪ R树是B树向多维空间发展的另一种形式，是一种动态索引结构
▪ 对象空间按范围划分，每个结点对应一个区域▪ 由中间节点和叶节点组成
▪ 非叶结点存储其所有子结点的区域范围，所有子结点的区域都落在它的区域范围之内▪ 叶结点中存储其区域范围之内的所有空间对象的最小外接矩形（MBR

▪ 每个结点所能拥有的子结点数目有上、下限
▪ 下限保证对磁盘空间的有效利用
▪ 上限保证每个结点对应一个磁盘页
▪ 当新增操作导致某结点需要的空间大于一个磁盘页时，将该结点一分为二
▪ R树是一种动态索引结构，即：它的查询可与新增或删除同时进行

▪ 最小外接矩形MBR是包围数据，且平行于X，Y轴的最小外接矩形（以二维为例）
▪ MBR有什么作用？
▪ 数据的分布是不规则的，而MBR是平行于X，Y轴的规则图形，针对这样的矩形进行几何上的任何判断更加简单
▪ R-tree是B树在高维数据空间的扩展
▪ 是一种高度平衡树
▪ 用原始数据的最小边界矩形表示数据
▪ 删除、更新等操作都类似B树
▪ 有效支持的数据维数20维以下
▪ 可以进行点查询和范围查询
▪ 影响查询效率的主要因素
▪ 重叠区域：导致查询时遍历多个路径
▪ 死空间：导致查询时遍历不必要的路径
▪ 在构建R-tree时要尽量减少重叠区域和死区域的面积
分裂的原则：尽量减少对分裂后的两个节点进行查询操作
▪ 两个子节点所覆盖的区域面积之和尽量的小
▪ R-tree算法主要问题：
▪ 节点存在重叠现象，导致查询时可能要遍历多条路径，甚至是全部路径
▪ 当数据维度增大时，重叠现象迅速恶化，导致查询性能急剧下降

▪ R±tree
▪ 基本结构与R-tree相同
▪ 兄弟节点之间的MBR不允许重叠
▪ 一个数据可以被分割存储在不同的叶子节点中
▪ R±tree具有更好的查询性能，但需要更多的存
储空间
▪ 新增和删除操作的效率较低

▪ k-d-tree
▪ 一种由二叉搜索树推广而来的用于多维检索的树的结构形式（k即为空间的维数），主要应用于多维空间关键数据的搜索
▪ 传统二叉树无法适应多维数据的需求
▪ 与二叉搜索树不同的是它的每个结点表示k维空间的一个点，用一个k-1维超平面将节点所表示的k维空间分成两个部分
▪ N mod k

▪ VA-File (Vector Approximation File)
▪ 一种针对高维空间中矢量（点数据）的快速近似查询方法
▪ 通过数据压缩，近似表示高维矢量数据，减少磁盘代价

▪ VA-File的K近邻查询
▪ 1. 根据查询矢量确定匹配范围的下界和上界
▪ 2. 对候选矢量计算与查询矢量间的距离并排序 得到K近邻结果
▪ 量化精度影响匹配效果
▪ 量化越精确，第一步过滤效果越好，但代价更高
▪ 反之会影响第一步的查询精度
▪ 需要一个折中策略来确定量化精度

▪ iMinMax(θ)
▪ 一种基于降维的高维索引方法
▪ 将高维空间的点用其在所有维上的最大值或最小值表示，即利用边界近似的方法将高维数据映射到一维，然后用B±tree进行索引
▪ 通过调整参数θ，使算法适应不同的数据分布

▪ 基于聚类的索引结构
▪ 高维数据的分布具有聚集的特点
▪ 存在的问题：
▪ 聚类算法复杂度较高
▪ 聚类效果不理想