玩转Random的正确姿势-编程知识

一、关于java.util.Random

我们知道，在数学领域里面0到1之间的小数是无穷无尽的，所以如果从数学角度上来讲，要计算0到1之间某个小数出现的概率是不现实的，但是作为计算机领域的人员应该会注意到，大多数编程语言中随机数的出现是等概率的，为什么会这样呢，因为在计算机里面，是有精度限制的，所以能表示的小数范围是有限的，而不是无穷无尽的，那么各个语言在设计的时候，通过一定的设计就可以实现等概率返回某个小数，下面以java语言为例

在 Java 中，java.util.Random 类的随机数生成是基于伪随机数生成器（Pseudorandom Number Generator，PRNG）实现的。PRNG 是一种算法，通过使用一个种子（seed）来生成一系列看似随机的数字序列。这些数字序列在统计上表现为随机分布，但实际上是确定性的，因为它们是根据初始种子和固定的算法生成的。

java.util.Random 类使用一个称为线性同余生成器（Linear Congruential Generator，LCG）的算法来生成伪随机数。LCG 算法通过以下公式生成随机数序列：

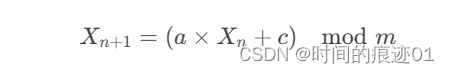
其中：

(X_n) 是前一个随机数
(X_{n+1}) 是下一个随机数
(a)、(c) 和 (m) 是算法中的参数

在 java.util.Random 类中，这些参数被固定为以下值：

(a = 25214903917)
(c = 11)
(m = 2^{48})

Random 类的 nextDouble() 方法会生成一个 48 位的随机数，然后将其转换为 0 到 1 之间的双精度浮点数。由于使用固定的算法和参数，因此 Random 类生成的随机数序列是可预测的，但在统计上表现为随机分布，满足一般应用中对随机性的需求。

下面我们来验证一下java.util.Random是否是真正的等概率返回小数的

    static int times = 1000000;static double x = 0.7;static int count = 0;/*** 一次方：0~x上的小数出现的概率：验证Math.random()等概率返回小数*/private void once() {for (int i = 0; i < times; i++) {if (Math.random() < x) {count++;}}System.err.println((double) count / times);}

通过运行once方法会发现输出的值约等于0.7，也就说明确实是等概率

二、基于java.util.Random衍生的一些算法题

题一：要求实现0到x（x小于1）范围内，每个小数出现的概率是x的平方，比如x=0.7的时候，那么返回0.7的概率是0.49，也就是0.7的平方，代码实现如下：

    private void two() {for (int i = 0; i < times; i++) {if (Math.max(Math.random(), Math.random()) < x) {count++;}}System.err.println((double) count / times);}

运行结果就不在这里展示了，大家可以自行运行测试一下，为什么这个代码可以实现以x的平方概率返回x的值呢，我们知道max函数是返回两个数中较大的那一个，那么要满足Math.max(Math.random(), Math.random())返回的值小于x，那么就必须连续两次调用Math.random()返回的值都落在0到x的范围，比如当x=0.7的时候，两次Math.random()都返回0.5那么就满足条件，只要有一个返回大于0.7的值，那么max返回的值就会大于x，所以这个就实现了以x的平概率返回x的值

题二：以x的三次方概率返回x的值

这个题的思路跟题一的思路是一样的，也就是要同时满足三次Math.random()的值都落在0到x的范围内，那么只需要对其中一个Math.random()再取一次max即可，代码如下：

    /*** 一次方：0~1上的小数出现的概率为x的三次方*/private void three() {for (int i = 0; i < times; i++) {if (Math.max(Math.max(Math.random(), Math.random()), Math.random()) < x) {count++;}}System.err.println((double) count / times);}

题三：给你一个已经实现好的函数f，它可以等概率返回1到5之间的整数，也就是等概率返回1,2,3,4,5，要求利用f函数等概率返回1到7之间的整数，也就是等概率返回1,2,3,4,5,6,7，f函数的内容不能修改

我们知道Random是可以等概率返回0到1之间的小数的，那么如果能够实现等概率返回0到6之间的小数，那么要等概率返回1到7之间的整数就很简单了，首先第一步，我们来实现f函数的功能：

   /*** 等概率返回1到5之间的整数*/private static int f() {return (int) (Math.random() * 5) + 1;}

如果能直接使用random的话就很简单了，但是现在要求只能使用f函数，于是我们可以换一种思路，能不能通过f函数来等概率返回0和1呢，如果能的话，那么我们就可以等概率返回一个三个二进制位表示的整数，也就是0到7的范围（000~111）

f函数是等概率返回12345的，要想等概率返回0和1，我们可以把1和2归纳为一组，表示0,4和5归纳为一组，表示1，多出来的这个3就不能用了，就要强制重新通过f返回一个新的数据，直到不等于3，这样就相当于是把3的那20%的概率强制平均到1245上了，实现代码如下：

    /*** 利用f函数等概率返回0和1*/private int eqauls0And1() {int tmp = f1To5();while (tmp == 3) {tmp = f1To5();}return tmp < 3 ? 0 : 1;}

我们用eqauls0And1来获取一个有三个二进制位标示的整数，也就是下面的代码：

(eqauls0And1() << 2) + (eqauls0And1() << 1) + (eqauls0And1() << 0)

这个就可以等概率返回000~111之间的整数，但是我们的目标是0到6，多了一个7（也可以说0是多余的），思路同前面一样，遇到0或者是7的时候强制重来，下面以7为例：

    /*** 利用eqauls0And1从000到111等概率返回，也就是0到7等概率返回*/private int OOO_to_111() {int tmp = (eqauls0And1() << 2) + (eqauls0And1() << 1) + (eqauls0And1() << 0);return tmp;}/*** 类似eqauls0And1的思想等概率返回0到6的整数*/private int O_to_6() {int tmp = OOO_to_111();while (tmp == 7) {tmp = OOO_to_111();}return tmp;}

最后只需要将O_to_6返回的结果加1就能达到目的了，如果是把0当做多余的那个，那么就不用加1了，代码就不在这里展示了，只需要把O_to_6中7改成0即可

题四：已知一个函数f是不等概率返回0和1，要求里用f函数实现等概率返回0和1，同样不能修改f函数的逻辑

假设f函数返回0的概率是0.7，返回1的概率是0.3，那么f函数逻辑如下

    /*** 不等概率返回0和1*/private int notEquals0And1() {return Math.random() < 0.7 ? 0 : 1;}

解题思路跟前面一样，就是想办法把不等概率通过强制重做转换为等概率，用一个二进制位肯定是做不到了，于是我们可以想到用两个二进制位，那么返回两个二进制位的概率如下：

00	0.7*0.7=0.49
01	0.7*0.3=0.21
10	0.7*0.3=0.21
11	0.3*0.3=0.09

我们可以看到返回01和10的概率是相等的，那么只需要把返回00和11的时候强制重来，就可以了，代码如下：

第一种：连续重做两次

    private int equals0And1() {int a = notEquals0And1();int b = notEquals0And1();while (a == b) {a = notEquals0And1();b = notEquals0And1();}return a == 1 ? 0 : 1;}

第二种，像前面那种利用二进制来实现：

 (notEquals0And1() << 1) + (notEquals0And1() << 0)

如果这个返回的数是0或者3就强制重做，其实效果同上面是一样的:

    private int equals0And1V2() {int a = (notEquals0And1() << 1) + (notEquals0And1() << 0);while (a == 0 || a == 3) {a = (notEquals0And1() << 1) + (notEquals0And1() << 0);}return a == 1 ? 0 : 1;}