LeetCode 2482.行和列中一和零的差值-编程知识

LeetCode 2482.行和列中一和零的差值

给你一个下标从 0 开始的 m x n 二进制矩阵 grid 。

我们按照如下过程，定义一个下标从 0 开始的 m x n 差值矩阵 diff ：

令第 i 行一的数目为 onesRowi 。
令第 j 列一的数目为 onesColj 。
令第 i 行零的数目为 zerosRowi 。
令第 j 列零的数目为 zerosColj 。
diff[i][j] = onesRowi + onesColj - zerosRowi - zerosColj
请你返回差值矩阵 diff 。

示例 1：

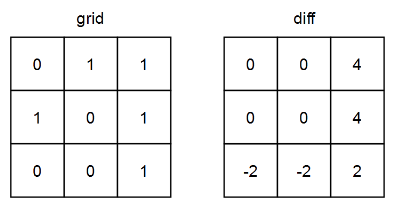
在这里插入图片描述

输入：grid = [[0,1,1],[1,0,1],[0,0,1]]
输出：[[0,0,4],[0,0,4],[-2,-2,2]]
解释：

diff[0][0] = onesRow0 + onesCol0 - zerosRow0 - zerosCol0 = 2 + 1 - 1 - 2 = 0
diff[0][1] = onesRow0 + onesCol1 - zerosRow0 - zerosCol1 = 2 + 1 - 1 - 2 = 0
diff[0][2] = onesRow0 + onesCol2 - zerosRow0 - zerosCol2 = 2 + 3 - 1 - 0 = 4
diff[1][0] = onesRow1 + onesCol0 - zerosRow1 - zerosCol0 = 2 + 1 - 1 - 2 = 0
diff[1][1] = onesRow1 + onesCol1 - zerosRow1 - zerosCol1 = 2 + 1 - 1 - 2 = 0
diff[1][2] = onesRow1 + onesCol2 - zerosRow1 - zerosCol2 = 2 + 3 - 1 - 0 = 4
diff[2][0] = onesRow2 + onesCol0 - zerosRow2 - zerosCol0 = 1 + 1 - 2 - 2 = -2
diff[2][1] = onesRow2 + onesCol1 - zerosRow2 - zerosCol1 = 1 + 1 - 2 - 2 = -2
diff[2][2] = onesRow2 + onesCol2 - zerosRow2 - zerosCol2 = 1 + 3 - 2 - 0 = 2
示例 2：

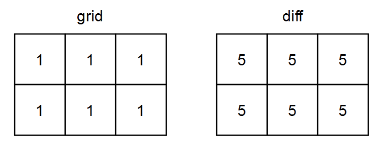
在这里插入图片描述

输入：grid = [[1,1,1],[1,1,1]]
输出：[[5,5,5],[5,5,5]]
解释：

diff[0][0] = onesRow0 + onesCol0 - zerosRow0 - zerosCol0 = 3 + 2 - 0 - 0 = 5
diff[0][1] = onesRow0 + onesCol1 - zerosRow0 - zerosCol1 = 3 + 2 - 0 - 0 = 5
diff[0][2] = onesRow0 + onesCol2 - zerosRow0 - zerosCol2 = 3 + 2 - 0 - 0 = 5
diff[1][0] = onesRow1 + onesCol0 - zerosRow1 - zerosCol0 = 3 + 2 - 0 - 0 = 5
diff[1][1] = onesRow1 + onesCol1 - zerosRow1 - zerosCol1 = 3 + 2 - 0 - 0 = 5
diff[1][2] = onesRow1 + onesCol2 - zerosRow1 - zerosCol2 = 3 + 2 - 0 - 0 = 5

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 105
1 <= m * n <= 105
grid[i][j] 要么是 0 ，要么是 1 。

法一：预处理一下nums，找出每行和每列1的个数，然后模拟即可：

class Solution {
public:vector<vector<int>> onesMinusZeros(vector<vector<int>>& grid) {int rowNum = grid.size();int colNum = grid[0].size();vector<int> rowOne(rowNum);vector<int> colOne(colNum);for (int i = 0; i < rowNum; ++i){for (int j = 0; j < colNum; ++j){if (grid[i][j] == 1){++rowOne[i];++colOne[j];}}}vector<vector<int>> ans;for (int i = 0; i < rowNum; ++i){ans.push_back({});for (int j = 0; j < colNum; ++j){int curAns = rowOne[i] + colOne[j] - (colNum - rowOne[i]) - (rowNum - colOne[j]);ans.back().push_back(curAns);}}return ans;}
};

此算法时间复杂度为O(mn)，空间复杂度为O(m+n)。

法二：法一基础上的小优化，我们预处理时，遇到1增加本行和本列的1的数量，遇到0时减少本行和本列1的数量，因为最后的结果中的某个元素可以看做本行1的个数减去本行0的个数加上本列1的个数减去本列1的个数：

class Solution {
public:vector<vector<int>> onesMinusZeros(vector<vector<int>>& grid) {int rowNum = grid.size();int colNum = grid[0].size();vector<int> rowOne(rowNum);vector<int> colOne(colNum);for (int i = 0; i < rowNum; ++i){for (int j = 0; j < colNum; ++j){if (grid[i][j] == 1){++rowOne[i];++colOne[j];}else{--rowOne[i];--colOne[j];}}}vector<vector<int>> ans;for (int i = 0; i < rowNum; ++i){ans.push_back({});for (int j = 0; j < colNum; ++j){ans.back().push_back(rowOne[i] + colOne[j]);}}return ans;}
};