这篇博客通过手动创建的一个简单二叉树,实现二叉树遍历,返回节点,叶子个数,查找结点等相关操作。
1. 二叉树的概念
二叉树不为空时,由根节点,左/右子树组成,逻辑结构如下,当二叉树为空时称为空树。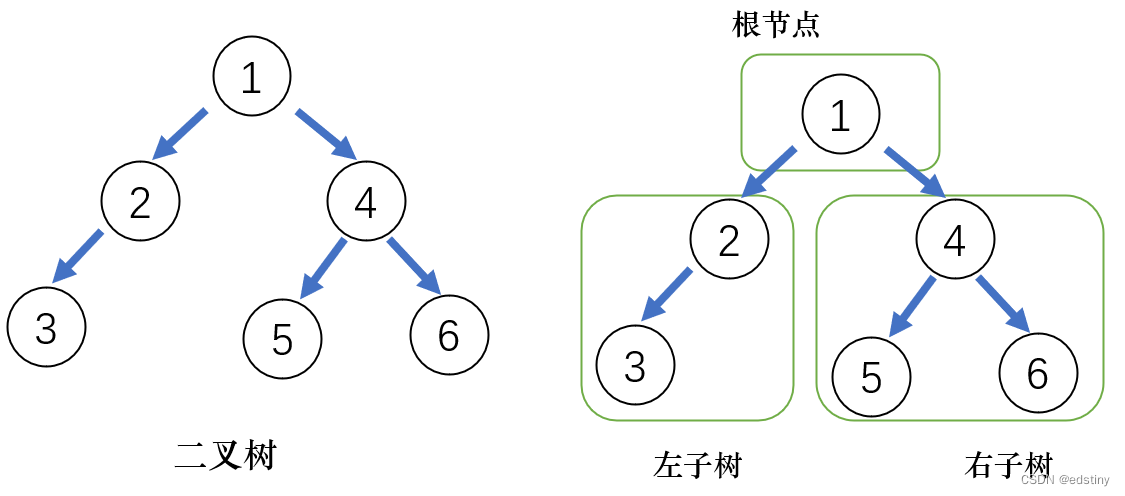
我们可以看到,左子树同样可以看作是根节点和左右子树构成,因此二叉树的基本操作需要利用递归的方式得以实现。此处需要注意的是,每次递归返回值不一定是传递给最外层的。
2.二叉树的遍历
二叉树的遍历按照规则分为三种情况,分别是前序遍历,中序遍历以及后序遍历。前序遍历先访问根节点再访问左右子树,中序遍历先访问左子树,再访问根节点和右子树,后序遍历先访问左右子树最后访问根节点。因此根据上述二叉树的排列不难写出二叉树的三种遍历情况,我们将NULL简写成 N,如下图所示:
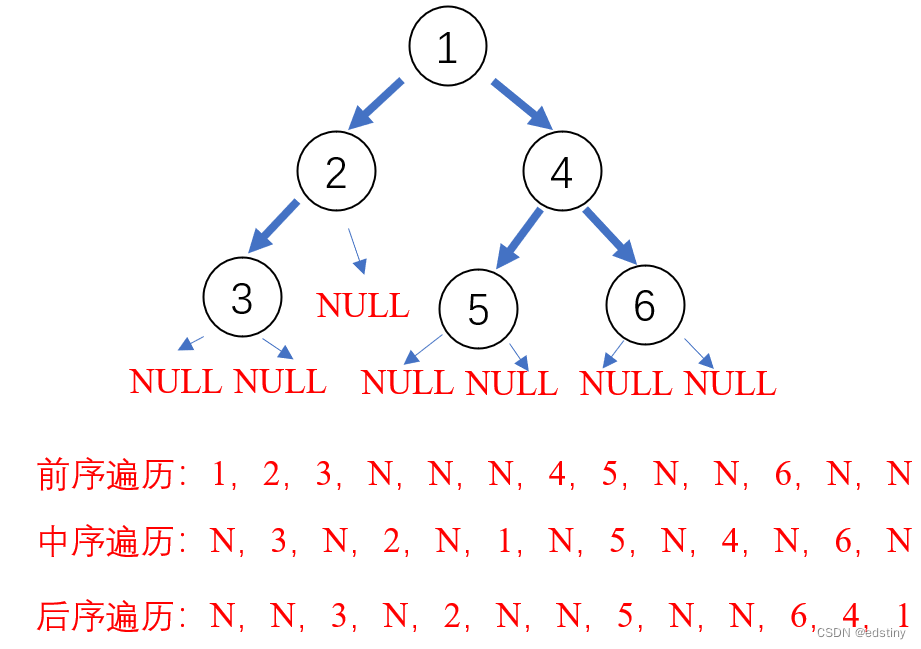
在代码实现的过程中,我们先创建节点,在更改节点的指向,即可实现我们需要的上述的结构:
typedef int BTDataType;typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;BTNode* BuyNode(BTDataType x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc fail");return;}newnode->left = NULL;//初始化newnode->right = NULL;newnode->data = x;return newnode;
}BTNode* creatBinaryTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}
实现三种情况的遍历,我们可以通过递归实现,因为二插树可以分成根节点和左右子树,左右子树又可以分为根节点和下一个左右子树,直到叶节点。代码如下:
void preorder(BTNode* root) //前序遍历
{if (root == NULL) {printf("N ");return;}printf("%d ",root->data);preorder(root->left);preorder(root->right);
}
void Inorder(BTNode* root)//中序遍历
{if (root == NULL){printf("N ");return;}Inorder(root->left);printf("%d ", root->data);Inorder(root->right);
}
void postorder(BTNode* root)//后续遍历
{if (root == NULL){printf("N ");return;}postorder(root->left);postorder(root->right);printf("%d ", root->data);
}
3.二叉树结点的个数
求二叉树结点的个数,也是同样的道理,计算左右子树结点之和+1即可。
int BTreeSize(BTNode* root)//分治求节点的个数
{if (root == NULL){return 0;}return BTreeSize(root->left)+ BTreeSize(root->right) + 1;
}
4.求叶子节点的个数
叶子节点的左右子树均为空,按照这个结束条件设计递归即可。
int BTreeLeafSize(BTNode* root)//求叶子节点的个数
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return BTreeLeafSize(root->left) + BTreeLeafSize(root->right) ;
}
5. 二叉树的最长路径
将求最长路径问题分成求左右子树的最长路径,之后取大的值即可。
int BTreeHeight(BTNode* root)//最长的路径
{if (root == NULL)//一定要判空树{return 0;}int leftHeight = BTreeHeight(root->left);int rightHeight = BTreeHeight(root->right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}
6. k层二叉树的节点个数
k层二叉树的节点个数问题可转化成左右节点k-1层节点个数之和,递归的结束条件是k == 1且节点不为空,以及节点为空。
int BTreeLevelKsize(BTNode* root,int k)//子问题,结束条件
{assert(k>0);if (root == NULL){return 0;}if (k == 1){return 1;}return BTreeLevelKsize(root->left, k - 1) + BTreeLevelKsize(root->right, k - 1);}
7. 查找值并返回节点的地址
依然是递归调用,分为左右节点。
BTreeFind(BTNode* root, BTDataType x)
{if (root == NULL){return NULL;}if (root->data == x){return root;}BTNode* ret1 = BTreeFind(root->left, x); if (ret1){return ret1;}BTNode* ret2 = BTreeFind(root->right, x); if (ret2){return ret2;}return NULL;
}
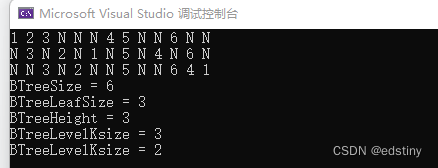
8. 结果
int main()
{BTNode* root =creatBinaryTree();preorder(root);printf("\n");Inorder(root);printf("\n");postorder(root);printf("\n");printf("BTreeSize = %d\n", BTreeSize(root));printf("BTreeLeafSize = %d\n", BTreeLeafSize(root));printf("BTreeHeight = %d\n", BTreeHeight(root));printf("BTreeLevelKsize = %d\n", BTreeLevelKsize(root,3));printf("BTreeLevelKsize = %d\n", BTreeLevelKsize(root, 2));return 0;
}