代码随想录(day2)——数组-编程知识

Leetcode.977 有序数组的平方：

题目如下：

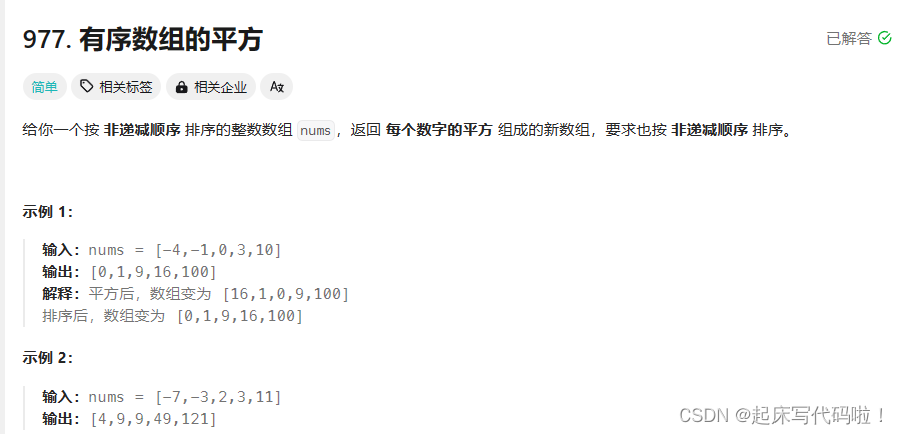
对于本题，可以采用双指针的方法进行解答，如果笔者写的几篇关于题解的文章有幸被读者浏览的话，会发现，针对数组问题，很大一部分是使用双指针来解决的。因此，在后续的文章中，将会专门有一篇文章来对于 $Leetcode$ 中关于双指针的经典题目进行解析。

本题涉及的双指针原理并不复杂，具体如下：

由于数组中存在负数，并且，题目中给出了给定的整数数组是按照非递减顺序排序的，因此，在抛去两个元素相等的情况下，数组中的第一个元素，一定是数组中最小的负数，数组中最后一个元素，绝对是数组中最大的一个正数。但是，在经过平方处理后，二者的大小关于有可能发生改变。但是，二者平方后，绝对是数组平方处理后，最大的两个数。

介于这个思路，可以定义两个指针 $left,right$ ，分别指向给定数组的第一个元素和最后一个元素。再利用创建一个一样大的数组，这里命名为 $v$ ，由于题目要求，新数组也需要非递减顺序，因此，再顶一个一个变量 $k$ ， $k=nums.size()-1$ 。

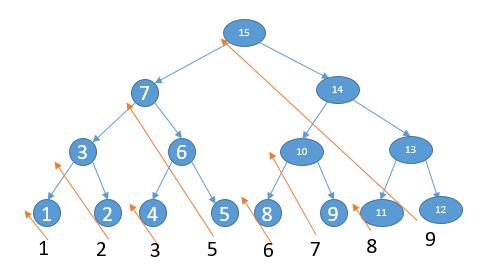
在最开始，比较 $nums[left]*nums[left]$ 和 $nums[right]*nums[right]$ ，找出二者较大的一个，并且将这个较大值赋值给 $v$ 的下标为 $k$ 的位置。具体原理可以由下面的流程图表示：

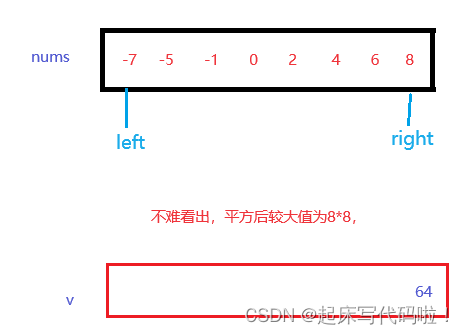
图中演示的是一种情况，即 $nums[right]*nums[right]> nums[left]*nums[left]$ 。

在进行完上述步骤后，令 $right--$ 。

如果是 $nums[left]*nums[left]>=nums[right]*nums[right]$ ，即上述情况的反情况，则在进行向 $v$ 赋值这一步骤后，需要令 $left++$ 。

并且，无论哪种情况，由于都需要在 $v$ 中插入元素，因此，在上述判断完成后，统一 $k--$ 。

不难看出，上述过程有点类似二分查找中对于 $left,right$ 的使用。在本题，也需要利用循环进行反复的判断以及插入元素。对于循环的结束条件，为 $left<=right$ 。因为对于图中的情况，当 $left==right$ ，此时两个指针均指向元素 $0$ ，并且元素 $0$ 并没有在 $v$ 中进行赋值。所以，为了避免这种情况，需要对于两个指针相等的情况也作一次处理。

对应代码如下：

class Solution {
public:vector<int> sortedSquares(vector<int>& nums) {vector<int> v;int k = nums.size()-1;v.resize(k+1,0);int left = 0,right = nums.size()-1;while(left <= right){if(nums[left]*nums[left] > nums[right]*nums[right]){v[k] = (nums[left]*nums[left]);left++;}else if( nums[left]*nums[left] <= nums[right]*nums[right]){v[k] = nums[right]*nums[right];right--;}k--;}return v;}
};

运行结果如下：

Leetcode.59 螺旋矩阵Ⅱ：

题目如下：

59. 螺旋矩阵 II - 力扣（LeetCode）

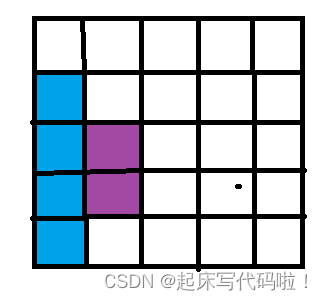
本题主要考察对于数组临界条件的控制。并且，在采取遍历并且给数组赋值的这一步中，如果没有想到正确的方法，则临界条件造成的题目的复杂度会大大上升，为了便于控制数组，文章采取了每次初始化 $n-1$ 个元素的方法，具体可以由下图表示：

如上图所示，对于螺旋矩阵的四个边，需要分四次进行处理，为了降低临界条件对于复杂度的影响，在处理螺旋矩阵的第一行时，只向里面填充四个元素，即 $n-1$ 个元素。对于第五个元素，则留在对于最后一列的元素进行处理时处理。对于其他的边原理均相同。

在填充完数组的最外层后，在填充第二层元素时，需要注意，此时第一个需要被填充的元素的数组下标为 $[1,1]$ ，而在填充第一层元素时，第一个被填充的元素下标为 $[0,0]$ ，因此，为了方便控制，可以单独创建两个变量用于表示这一层螺旋的起始元素的地址，再每经过一次螺旋的填充后，令这两个变量的值 $++$ 即可。为了方便表示，这里将这两个元素命名为 $startx,starty$ 分别用于表示起始元素的行，列。

前面提到，因为每次填充的元素个数为 $n-1$ 个，但是，这也仅限于第一行，因为第一行需要填充 $n-1$ 个元素，例如上图中，第一行填充 $4$ 个元素。但是到了第二次螺旋，由于起始地址改变了，并且需要填充内层元素，所以，对于第一行，第二行元素的填充，可以表示为 $n-starty-m$ ,其中 $m=1,2,3......$ 为了方便表示，在下面的给出的代码中，用 $offest$ 表示 $m$ 。

由此，上面给出的文字说明，给出了对于填充元素的临界条件，即：第一个被填充和最后一个被填充的位置的下标。不过上面说到，针对一个循环，需要进行四次处理，下面将分别给出处理方法：

如上图所示，给出了对于行元素的初始化，前面说到，为了更好的控制第一个被填充的元素的下标，创建了两个变量 $startx,starty$ 。对于第一行元素的填充，通过观察不难发现，行数不会改变，一直等于 $startx$ ，但是列数在改变。所以，针对这种情况，可以由下面的代码进行处理：

for(j = starty; j < n-offest; j++)
{nums[i][j] = count++;
}

其中 $count = 1$ ，每次进行填充后 $count$ 会增大。

对于本部分元素的填充，是列不变，但是行数在不停改变，在上一部分的元素填充中，用于表示列的变量 $j$ 此时恰好位于最后一列。因此，只需要定义 $i=startx$ ，改变 $i$ 即可。具体对应代码如下：

for i = startx; i < n-offest; i++)
{nums[i][j] = count++;
}

对于本部分元素的填充，只需要改变 $j$ 即可。但是前面部分的填充中， $j$ 恰好位于最后一列， $i$ 恰好处于最后一行，因此，只需要改变 $j$ 即可。具体代码如下：

for(; j > starty; j--)
{nums[i][j] = count++;
}

对于本部分元素的填充，此时 $j$ 恰好处于第一列， $i$ 恰好处于最后一行，因此对于代码如下：

for(; i > startx; i--)
{nums[i][j] = count++;
}

在一次螺旋走完后，需要改变 $startx,starty,offest$ 的大小，即全部 $++$ 。

对于本处给出的图形，不难看到， $n$ 是一个奇数，因此，对于 $n$ 为奇数的螺旋矩阵，会单独空一中间的位置没有被元素填充，具体可以由图片表示：

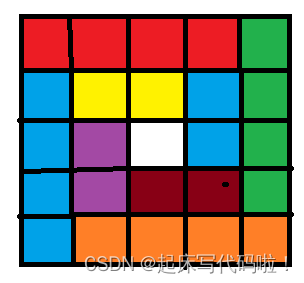
对于此处的坐标，可以用 $n/2$ 表示，因此，在进行循环填充后，还需要判断 $n$ 如果为奇数，则额外对中心的位置进行处理。对应代码如下：

class Solution {
public:vector<vector<int>> generateMatrix(int n) {vector<vector<int>> nums;nums.resize(n);for(int i = 0; i <n; i++){nums[i].resize(n,0);}//控制循环次数int k = n/2;//控制初始点位置int startx = 0,starty = 0;int count = 1;int offest = 1;int mid = n/2;int i = 0,j = 0;while(k--){i = startx,j = starty;for(j = starty; j < n-offest; j++){nums[i][j] = count++;}for(i = startx; i < n-offest; i++){nums[i][j] = count++;}for(;j > starty; j--){nums[i][j] = count++;}for(;i > startx; i--){nums[i][j] = count++;}startx++;starty++;offest+=1;}if(n%2 == 1){nums[mid][mid] = count;}return nums;}
};

运行结果如下：

Leetcode.209 长度最小的子数组：

209. 长度最小的子数组 - 力扣（LeetCode）

本题可以划分于滑动窗口这个类型，对于此类型的题目，在后续将会有专门的博客进行介绍。对于滑动窗口，起始可以看作一种特殊的双指针，对于之前的双指针，针对于目标都是单个具体的元素，但是对于滑动窗口，两个指针表示一个区间的起始位置和终止位置。

对于本题的解法，可以先创建两个指针，分别命名为 $start,end$ ，二者分别表示一段区间的起始位置和终止位置。由于题目要求需要与目标值 $target$ 进行比较，因此创建变量 $sum$ ，用于加和数组中的各个元素。如果 $sum < target$ ，则令 $end++$ ，且 $sum+=nums[end];$ 直到不满足 $sum<target$ 位置，对于题干中给出的一个数组，上述关系可以表示如下：

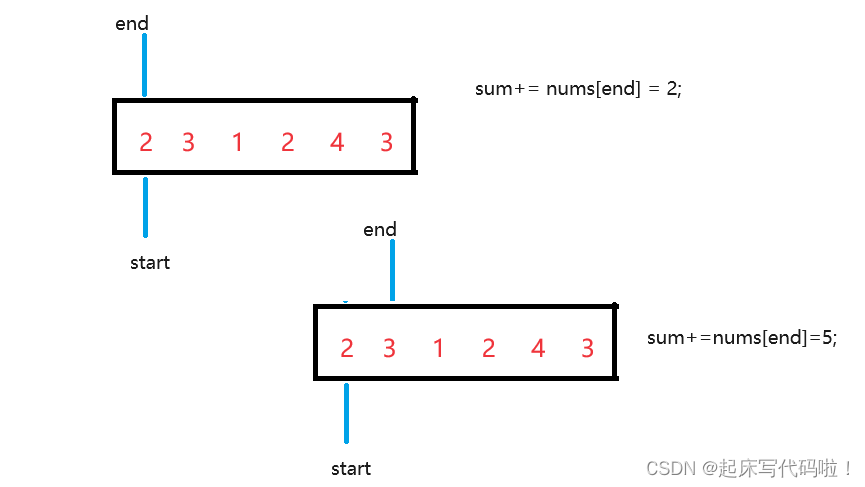
当 $end$ 指向数组中第四个元素时，即：

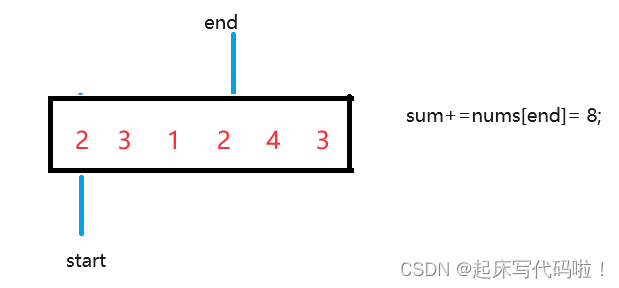
此时，得到了 $sum>target$ 的一个区间，但是，题目要求得到最小区间，因此，创建两个变量 $result,len$ 分别表示最小区间长度和用于进行比较的区间长度。但是，在第一次得到了 $len$ 时，由于 $result$ 不代表任何区间的长度，因此为了后续比较，这种情况下， $result$ 需要取最大值。

在得到了第一个满足大小关系的区间后，为了找到最小长度的区间，直接令 $start++$ ，即缩小这个区间的长度，并且令 $sum-=nums[start]$ 。再去进行比较，如果不满足大小关系，则令 $end$ 向后移动一位。然后再次进行判断，重复上述过程。

对于上述过程，下面将给出图片进行解释：

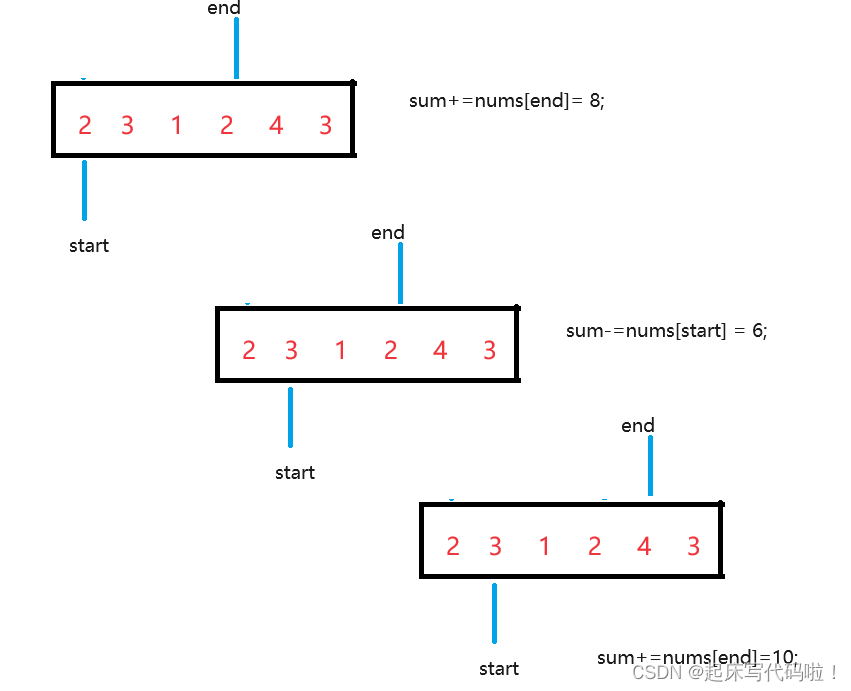
随后，每次找到了满足大小关系的区间，令 $result = min(result,len);$

具体代码如下：

class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int i = 0,j = 0;int sum = 0;int len = 0,result = 0;for(int j = 0; j < nums.size(); j++){sum += nums[j];while(sum >= target){len = j-i+1;if(i ==0){result = max(result,len);}result = min(result,len);sum -= nums[i];i++;}}return result;}
};