目录

题目介绍：

算法原理：

特殊位置处理：

代码实现：

---

题目介绍：

题目链接：. - 力扣（LeetCode）

算法原理：

这道题其实和我上一道题非常相似---寻找数组的中心下标，也是使用前缀和的思想，而这里需要改用前缀积：

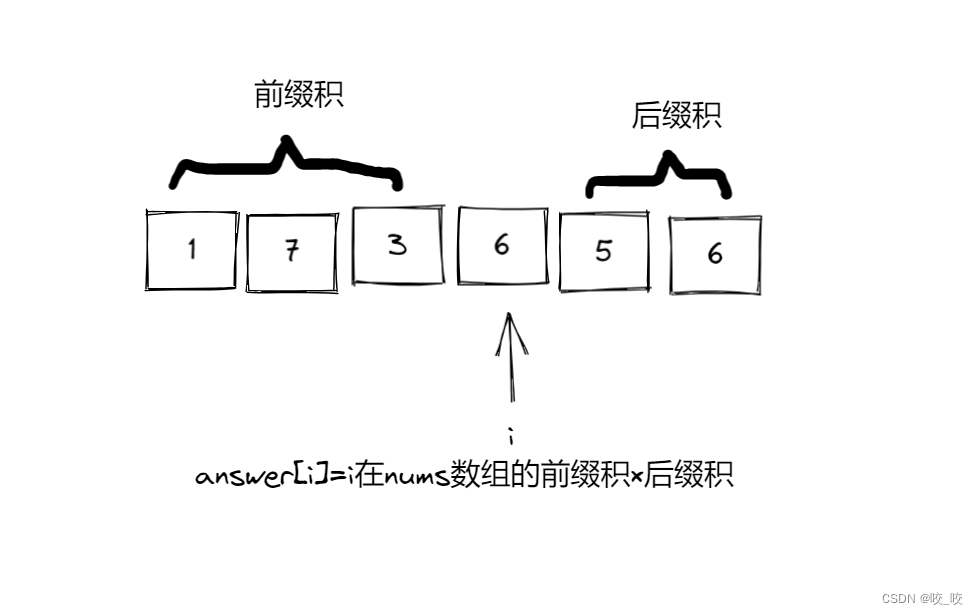
所以我们创建前缀积数组f，后缀积数组g：

f[i]表示nums数组（0~(i-1)）所有元素的积。(除自身外的前缀积）f[i]=f[i-1]*nums[i-1]

g[i]表示nums数组（(i+1)~(n-1)）所有元素的积。(除自身外的后缀积) g[i]=g[i+1]*nums[i+1]

特殊位置处理：

f[0]和g[n-1]，这两个位置要特殊处理一下，f[0]表示数组nums 0号位之前元素的积，可它之前没有元素，之前题目前缀和时我们都将它置为0，但这里不同，如果还是置为0的话，因为0乘任何数都是0，就会导致整个前缀积数组都变成0，所以为了不让它对后面的元素产生影响，我们应该把它置为1，g[n-1]同理。

 最后answer[i]=f[i]*g[i]

代码实现：

class Solution {
public:vector<int> productExceptSelf(vector<int>& nums) {//构建前缀积和后缀积数组int n= nums.size();vector<int> f(n,1),g(n,1);int i=1;for(i=1;i<n;i++){f[i]=f[i-1]*nums[i-1];}for(i=n-2;i>=0;i--){g[i]=g[i+1]*nums[i+1];}vector<int> answer(n);for(i=0;i<n;i++){answer[i]=f[i]*g[i];}return answer;}
};