K-Means算法:
K-means 是数据科学和商业的基本算法。让我们深入了解一下。
1. K-means是一种流行的用于聚类的无监督机器学习算法。它是用于客户细分、库存分类、市场细分甚至异常检测的核心算法。
2. 无监督:K-means 是一种无监督算法,用于没有标签或预定义结果的数据。目标不是预测目标输出,而是通过识别数据集中的模式、聚类或关系来探索数据的结构。
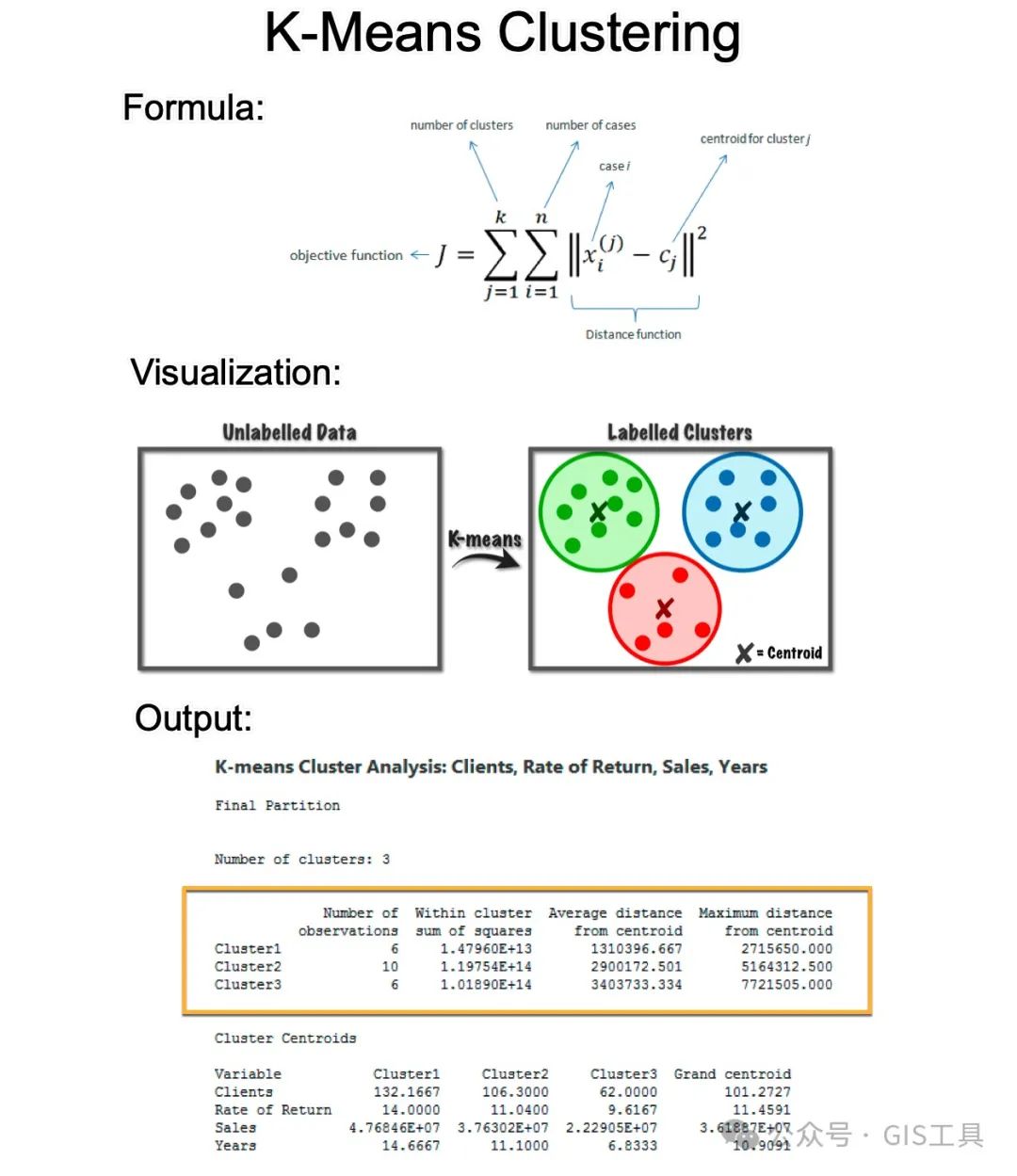
3. 目标函数:K-means 的目标是最小化簇内平方和(WCSS)。它通过一系列迭代步骤(包括分配和更新步骤)来实现这一点。
4. 分配步骤:在此步骤中,将每个数据点分配给最近的聚类质心。“最近”通常使用欧几里得距离来确定。
5.更新步骤:重新计算质心作为簇中所有点的平均值。每个质心是其簇中点的平均值。
6.迭代:重复分配和更新步骤,直到质心不再发生显着变化,表明集群稳定。此过程最大限度地减少了簇内方差。
7. 输出:聚类质心、标签和距离平方和。质心代表每个聚类中所有点的平均位置,对于解释聚类结果至关重要。标签是聚类分配。距离平方和是簇中每个点距簇质心距离的度量。
8. 评估。有多种评估 K 均值的方法。两种常见的方法是剪影评分法和肘部法。
9. Silhouette Score:该指标衡量数据点与其他集群相比与其自身集群的相似程度。轮廓得分范围从 -1 到 1,其中高值表示数据点与其自己的簇匹配良好,而与相邻簇匹配较差。
10. 肘部法:该方法涉及将惯性绘制为簇数量的函数,并在图中寻找“肘部”。下降率急剧变化的肘点对于簇数来说是一个不错的选择。
PostGIS 中的 K-Means 聚类操作及应用:
POSTGRESS是非常有名的开源数据库,POSTGIS是它的空间数据库扩展插件。相当于ARCGIS 中 ORACLE 和 SDE的关系。
点聚类是地理空间数据分析的常见任务,PostGIS提供了多种聚类功能,例如:
-
ST_ClusterDBSCAN
-
ST_ClusterKMeans
-
ST_ClusterIntersectingWin
-
ST_ClusterWithinWin
本文探讨了PostGIS 的 ST_ClusterKMeans函数的功能。K-Means 聚类作为一种对高维 LLM 嵌入进行分组的流行方式现在很流行,但它在较低维度的空间聚类中也很有作用。
ST_ClusterKMeans将对 2 维和 3 维数据进行聚类,并且当在点的“测量”维度中提供权重时,还会对点执行加权聚类。
为了尝试 K 均值聚类,我们需要一些点进行聚类,在本例中是 来自Natural Earth的1:10M 人口分布的数据。将其下载 GIS 文件并加载到数据库中,在此示例中使用 ogr2ogr。
ogr2ogr \-f PostgreSQL \-nln popplaces \-lco GEOMETRY_NAME=geom \PG:'dbname=postgres' \ne_10m_populated_places_simple.shp
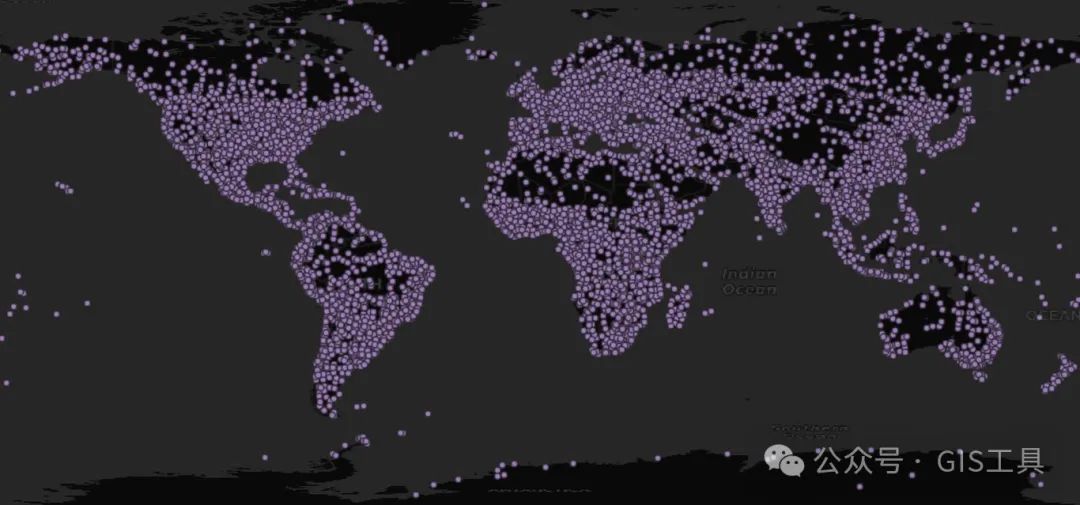
平面聚类(二维聚类)
二维空间中的简单聚类如下所示,使用 10 作为聚类数:
CREATE TABLE popplaces_geographic ASSELECT geom, pop_max, name,ST_ClusterKMeans(geom, 10) OVER () AS clusterFROM popplaces;
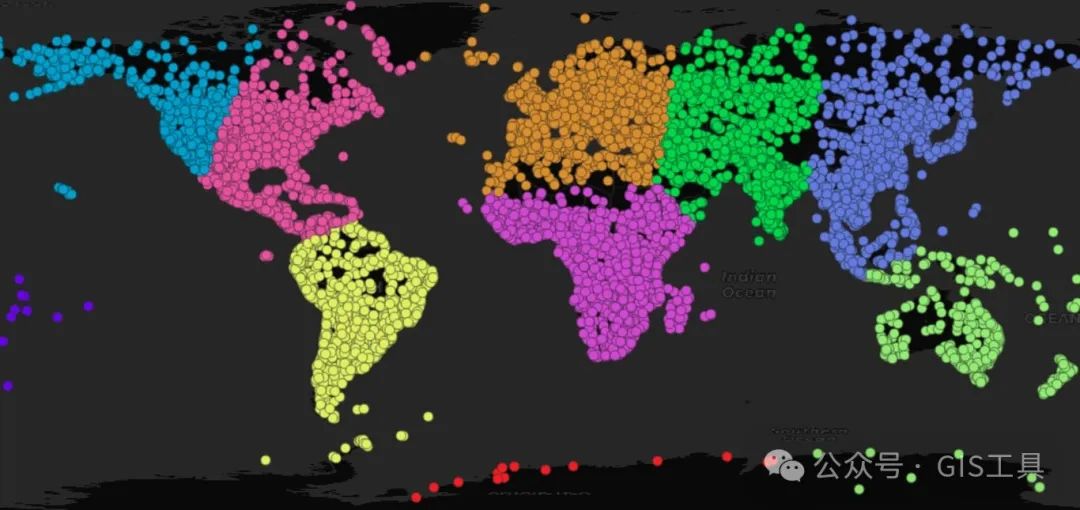
请注意,俄罗斯的部分地区与阿拉斯加聚集在一起,而大洋洲则被分开。这是因为我们将这些点的经度/纬度坐标视为在一个平面上,因此阿拉斯加距离西伯利亚非常远。
对于仅限于小区域的数据,诸如日期变更线分裂之类的影响并不重要,但对于我们的全球示例来说,却很重要。幸运的是,有一种方法可以解决这个问题。
地心聚类(三维聚类)
我们可以使用ST_Transform将原始数据的经度/纬度坐标转换为地心坐标系 。“地心”系统是一种原点为地球中心的系统,位置由距该中心的 X、Y 和 Z 距离定义。
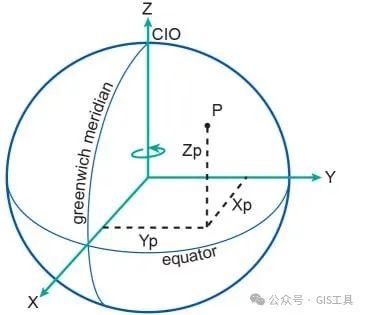
在地心系统中,日期变更线两侧的位置在空间中仍然非常接近,因此非常适合对全球数据进行聚类,而无需担心两极或日期变更线的影响。在本例中,我们将使用EPSG:4978作为我们的地心系统。
以下是转换为地心坐标的纽约坐标。
SELECT ST_AsText(ST_Transform(ST_PointZ(74.0060, 40.7128, 0, 4326), 4978), 1);POINT Z (1333998.5 4654044.8 4138300.2)SELECT ST_AsText(ST_Transform(ST_PointZ(74.0060, 40.7128, 0, 4326), 4978), 1);
POINT Z (1333998.5 4654044.8 4138300.2)这是在地心空间中执行的聚类操作。
CREATE TABLE popplaces_geocentric ASSELECT geom, pop_max, name,ST_ClusterKMeans(ST_Transform(ST_Force3D(geom),4978),10) OVER () AS clusterFROM popplaces;
结果看起来与平面聚类非常相似,但您可以在几个地方看到“整个世界”效应,例如澳大利亚和大洋洲的所有岛屿现在位于一个聚类中,以及西伯利亚和阿拉斯加之间的分界点星团已向西移动越过日期变更线。
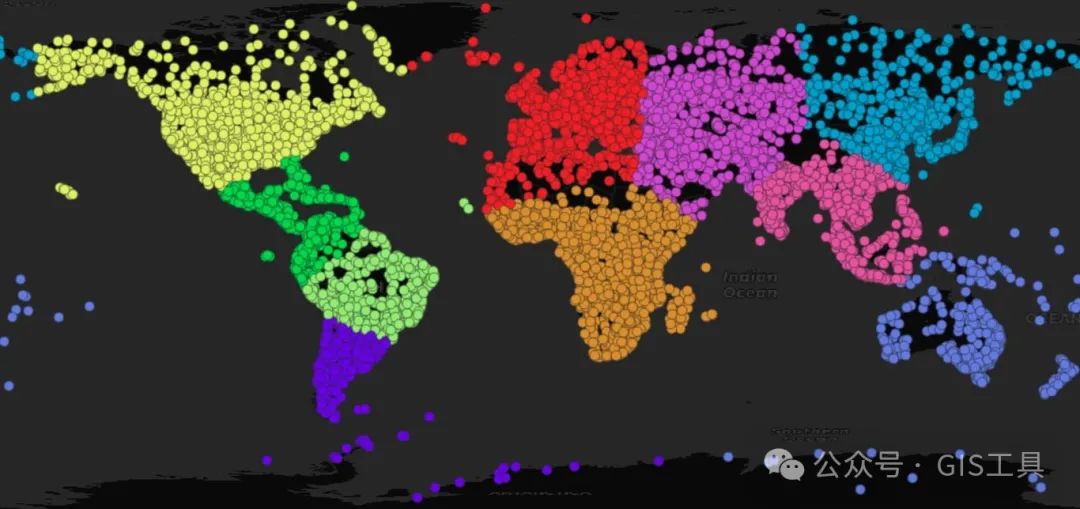
值得注意的是,尽管我们在二维中显示结果,但该聚类是在三个维度上执行的(因为地心坐标需要 X、Y 和 Z)。
加权聚类
除了朴素 k 均值之外, ST_ClusterKMeans还可以执行 加权 k 均值聚类,以使用输入点的“M”维度(第四维数据)增加额外信息来提高聚类质量。
由于我们有一个“人口稠密的地方”数据集,因此使用人口作为此示例的权重是有意义的。加权算法要求严格为正权重,因此我们过滤掉少数非正记录。
CREATE TABLE popplaces_geocentric_weighted ASSELECT geom, pop_max, name,ST_ClusterKMeans(ST_Force4D(ST_Transform(ST_Force3D(geom), 4978),mvalue => pop_max),10) OVER () AS clusterFROM popplacesWHERE pop_max > 0;
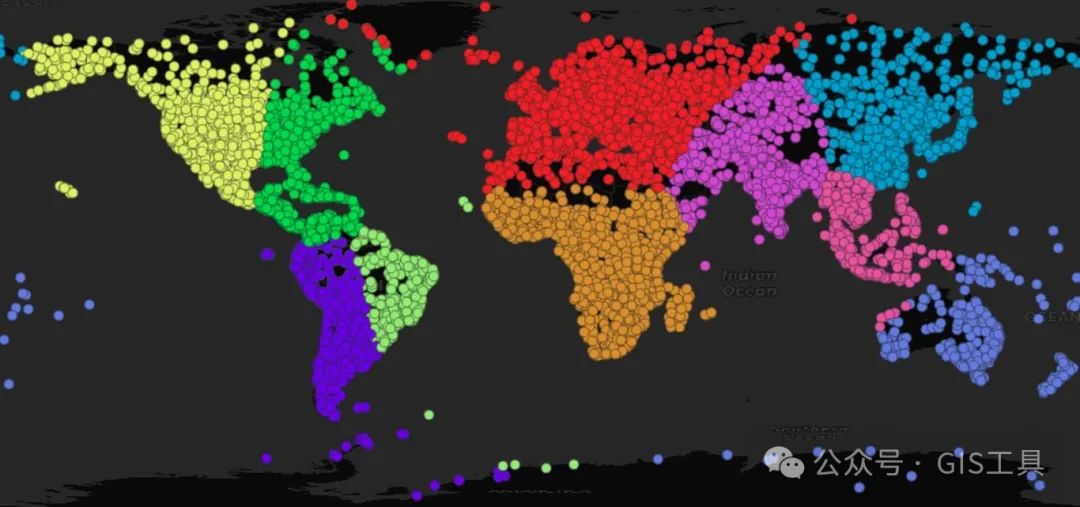
同样,差异是微妙的,但请注意印度现在是一个单一集群,巴西集群现在如何偏向人口稠密的东海岸,以及北美现在如何分为东部和西部。
![[蜥蜴书Chapter2] -- 创建测试集](https://img-blog.csdnimg.cn/direct/07db26abe754442ab84a55d0f1bb81cc.png)