3.2.1 约瑟夫环问题
【问题】 约瑟夫环问题(Josephds circle problem)由古罗马史学家约瑟夫提出,他参加并记录了公元66—70年犹太人反抗罗马的起义。约瑟夫作为一个将军,守住了裘达伯特城达47 天之久。在城市沦陷后,他和40名视死如归的将士在一个洞穴中避难,这些反抗者表决说“要投降毋宁死”。于是,约瑟夫建议每个人轮流杀死他旁边的人,而这个顺序是由抽签决定的。约瑟夫有预谋地抓到了最后一签,并且,作为洞穴中的两个幸存者之一,他说服了同伴一起投降了罗马。
【想法】 将参与抽签的人从1至n进行编号并构成一个环,从而将约瑟夫环问题抽象为如图3-1所示数据模型。假设密码是m, 从第1个人开始报数,报到m 时停止报数,报m的人出环;再从他的下一个人起重新报数,报到m时停止报数,报m的人出环。如此下去,直至所有人全部出环。当任意给定n和m后,求几个人出环的次序。
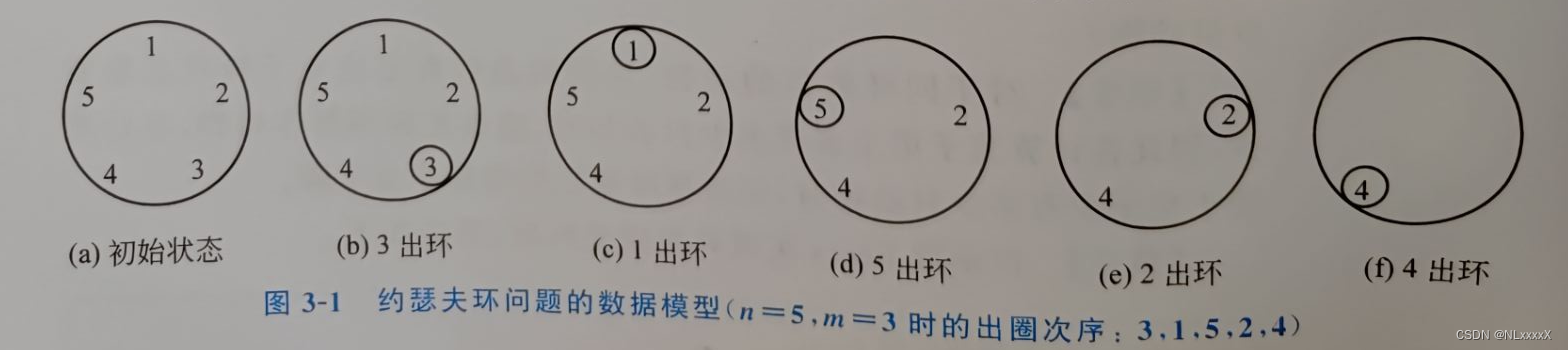
【算法】 设函数Joseph求解约瑟夫环问题,用数组r[n]存储n个人是否出列,下标表示人的编号,从1开始数到密码m 则将其出列。如果编号i的人出列则将数组r[i]置为1, 用求模运算%实现下标在数组内循环增1。算法如下。
算法:约瑟夫环问题Joseph
输入:参与游戏的人数n,密码 m
输出:最后一个出列的编号
1. 初始化数组 r[n]={0};
2.计数器 count=0;下标i=-1;出列人数 num-0;
3.重复下述操作直到数组r[n]仅剩一个人:
3.1 当count<m 时重复下述操作:
3.1.1 i=(i+1)% n;
3.1.2 如果r[i]未出列,则计数器count++;
3.2 令 r[i]=1;num++;
4.查找并返回仅剩的编号;
【算法分析】 步骤3在数组r[n]中反复查找待出列编号,外循环执行n-1次,内循环执行m次,时间复杂度为O(nXm)。
【算法实现】 设函数Joseph求解约瑟夫环问题,程序如下。
#include <iostream>
using namespace std;
int Joseph(int r[ ], int n, int m)
{
int count, i = -1, num = 0;
while (num < n - 1)
{
count = 0;
while (count < m) //查找报到m的人
{
i = (i+1) % n;
if (r[i] != 1) count++;
}
r[i] = 1; num++; //标记出列的人
}
for (i = 0; i < n; i++)
if (r[i] == 0) return i+1; //返回编号
}
int main( )
{
int n, m, x;
int r[10000] = {0};
cout<<"请输入人数和密码:";
cin>>n>>m;
x = Joseph(r, n, m);
cout<<"最后出列的人编号是:"<<x;
return 0;
}
3.2.2 埃拉托色尼筛法
【问题】埃拉托色尼筛法(the sieve of Eratosthenes)简称埃氏筛法,是古希腊数学家埃拉托色尼提出的算法,用于求一定区间内的所有素数。算法的基本思想是,从区间[1,n]内的所有数中去掉所有合数,剩下的就是所有素数。判断合数的方法是从2开始依次过筛,如果是2的倍数则该数不是素数,进行标记处理,直至将n/2过筛,将所有合数打上标记。
【想法】假设有一个筛子存放整数1~n,依次将2,3,5...的倍数筛去(标记),最后没有打上标记的数都是素数。埃拉托色尼筛法的计算过程如图所示。
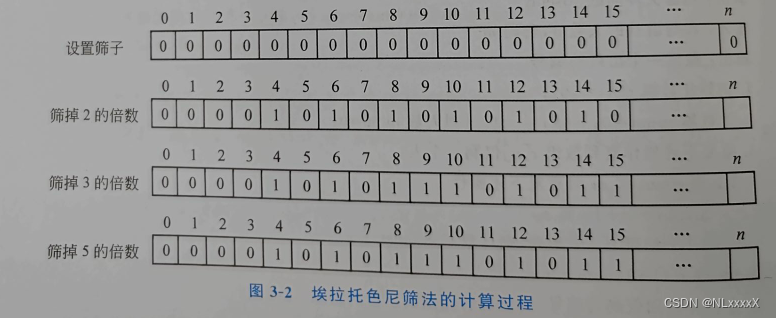
【算法】 设数组 A[n]表示筛子,元素值全部初始化为0,依次将下标是2,3,5...倍数的元素值置1进行标记处理,最后所有元素值为0对应的下标都是素数,算法如下。
算法:埃拉托色尼筛 EratoSieve
输入:待确定素数的范围n,数组 A[n]
输出:区间[1,n]的所有素数
1.循环变量i从2至n/2重复执行下述操作:
1.1 如果A[i]不等于0,说明整数i不是素数,转步骤1.3取下一个素数;
1.2将所有下标是i的倍数的元素值置为1;
1.3 i++;
2.输出数组 A[n]中所有元素值为0对应的下标;
【算法分析】 埃拉托色尼筛法实际上是一种空间换时间的算法优化,对于判断单个数的素数性质来说,相对于朴素的算法没有优化,但是对于求解某一区间的素数问题,埃拉托色尼筛法可以很快打印一份素数表,时间复杂度只有O(nlog logn)。
【算法实现】 设函数EratoSieve实现埃拉托色尼筛法,程序如下
#include <iostream>
using namespace std;
void EratoSieve(int A[ ], int n)
{
int i, j;
for (i = 2; i <= n/2; i++)
{
if (A[i] != 0) continue;
else
{
for (j = 2; i * j <= n; j++)
A[i*j] = 1;
}
}
}
int main( )
{
int n;
cout << "请输入判断素数的最大值(即区间):";
cin >> n;
if (n <= 0) {
cout << "无效的输入,请输入正整数。" << endl;
return 1;
}
int *A = new int[n + 1]{}; // 根据输入的 n 动态分配数组大小
EratoSieve(A, n);
cout << "以下是小于或等于 " << n << " 的素数:" << endl;
for (int i = 2; i <= n; i++) {
if (A[i] == 0) {
cout << i << " ";
// 添加空格以提高输出的可读性
}
}
cout << endl;
delete[] A; // 释放动态分配的数组内存
return 0;
}