Day 43

01. 最后一块石头的重量 II（No. 1049）

题目链接

代码随想录题解

<1> 题目

有一堆石头，用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。

每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

• 如果 x == y，那么两块石头都会被完全粉碎；
• 如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。

最后，最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下，就返回 0。

示例 1：

输入：stones = [2,7,4,1,8,1]
输出：1
解释：
组合 2 和 4，得到 2，所以数组转化为 [2,7,1,8,1]，
组合 7 和 8，得到 1，所以数组转化为 [2,1,1,1]，
组合 2 和 1，得到 1，所以数组转化为 [1,1,1]，
组合 1 和 1，得到 0，所以数组转化为 [1]，这就是最优值。

示例 2：

输入：stones = [31,26,33,21,40]
输出：5

提示：

• 1 <= stones.length <= 30
• 1 <= stones[i] <= 100

<2> 笔记

这道题其实和上一篇的 分割等和子集（No. 416） 非常类似，难点都是如何想出递归的思路。

在前面也提到过，动态规划其实就是用来求最值的，当看到可以利用最值求解的时候，就可以考虑递归的思路。

既然要求出什么时候两块石头能够相互抵消的最多，其实可以转换成 如何将这一堆石头分成两堆质量和 最 相近的石头；如果要分成最相近的两堆石头，那这个临界点就是这两堆石头重量 相等 的时候，即完全抵消的时候，也就是 约束 两堆重量最大值的条件有一条是：最大重量不能超过 sum / 2 也就是总重量的二分之一。

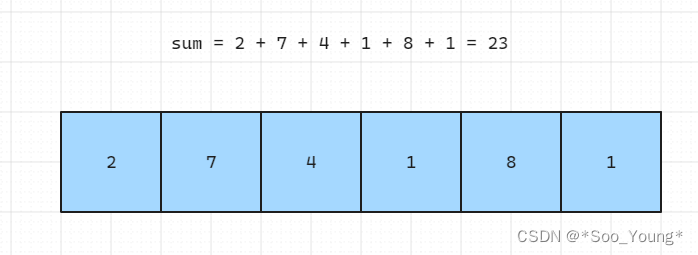
这时候得到了一堆中的最大重量，假设是 m 另一堆的最大重量也就是 sum - m，最终剩余的 重量 也就是
sum - 2 * m。

💡 说到这里其实很多人会思考如果 sum 是奇数的话，应该是向下取整还是向上取整呢？

• 其实是都可以的，比如上面那个例子当一堆中的物品取到可以将最大重量设定为 12 也可以设定为 11
• 站在总体的角度看，一堆中的重量想着 11 或者 12 靠近的时候，剩余的那一堆也是向它的目标靠近的
• 最终取得结果的时候就是整体的最优情况

但是如果求最大的那部分那最终的结果其实不好处理，因为这时候是依赖于 理论上的最大值 来进行限制的，只能说 其中一个部分 一定不会超过 这个理论上的最大值，但是另一部分却不一定，比如上题中的示例 2 ，它的两堆分别是 73 和 78，如果我们向上取整的话，其实最后还是要分辨 最终求得的部分是大的那一堆还是小的那一堆的，比如示例 1 的情况。

但如果向下取整就不会出现这种情况，因为这部分一定是小的那一堆；所以两种方式其实都可以，但是向下取整对结果的处理更加简单。

有一个限制（target）是 sum / 2，又有一堆东西可以去选择，这不正是一个背包问题嘛？

当遇到背包问题的时候不要去和背包问题类比，这样很容易把自己搞混乱，而是要像一开始接触到背包问题那样从头开始推导：限制值为 target ， dp[i][j] 是在当 前容量的限制下能够取得的最重的重量，对于一个石头可以选择 取或者不取，如果不取的话最终的重量其实就是 dp[i - 1][j] 如果取的话，最终得到的就是
dp[i - 1][j - stones[i]] + stones[j]，这样能得到和 01 背包 一样的递推公式。

之所以说不要尝试去类比，是因为其实很多 物品 是不具备 value 属性的，强行去类比反而会比较混乱，重要的是利用背包问题的思想去推导。

写出代码，本题的代码和背包问题几乎完全相同。

<3> 代码

二维数组的方法

class Solution {public int lastStoneWeightII(int[] stones) {int sum = 0; // 原本石头的总重量for (int i = 0; i < stones.length; i++) {sum += stones[i];}int[][] dp = new int[stones.length][sum/2 + 1];// 初始化 dp 数组for (int i = stones[0]; i < dp[0].length; i++) {dp[0][i] = stones[0];}for (int i = 1; i < stones.length; i++) {for (int j = 1; j < dp[0].length; j++) {if (j >= stones[i]) dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - stones[i]] + stones[i]);else dp[i][j] = dp[i - 1][j];}}return sum - 2 * dp[stones.length - 1][sum / 2];}
}   

滚动数组优化

class Solution {public int lastStoneWeightII(int[] stones) {int sum = 0; // 原本石头的总重量for (int i = 0; i < stones.length; i++) {sum += stones[i];}int target = sum / 2;int[] dp = new int[target + 1];// 初始化 dp 数组for (int i = stones[0]; i < dp.length; i++) {dp[i] = stones[0];}for (int i = 1; i < stones.length; i++) {for (int j = target; j >= stones[i]; j--) {dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);}}return sum - 2 * dp[target];}
}   

02. 目标和（No. 494）

题目链接

代码随想录题解

<1> 题目

给你一个非负整数数组 nums 和一个整数 target 。

向数组中的每个整数前添加 '+' 或 '-' ，然后串联起所有整数，可以构造一个 表达式 ：

• 例如，nums = [2, 1] ，可以在 2 之前添加 '+' ，在 1 之前添加 '-' ，然后串联起来得到表达式 "+2-1" 。

返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。

示例 1：

输入：nums = [1,1,1,1,1], target = 3
输出：5
解释：一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3

示例 2：

输入：nums = [1], target = 1
输出：1

提示：

• 1 <= nums.length <= 20
• 0 <= nums[i] <= 1000
• 0 <= sum(nums[i]) <= 1000
• -1000 <= target <= 1000

<2> 笔记

本题较容易想出来的肯定是回溯算法，即每个元素有两种情况，加上这个元素或者减去这个元素，但回溯算法的时间复杂度是指数级别的，可能不是最佳的解法；我会在代码区域贴上我的回溯算法示例。

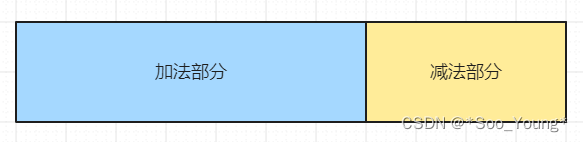
其实本题和上一题的思路比较类似，就是将这个集合去分成两部分，一部分是加法部分，另一部分是减法部分，只要将这两个部分相加得到的值是目标值即可。

这里设加法部分的总和为 m 减法部分的总和为 n，则可以得出 m - n = target，而又直到
m + n = sum，则可以有 m - (sum - m) = target 最终可以推导出 m = (target + sum) / 2 所以本题又变成了，从数组中选取元素，元素的总和能达到 (target + sum) / 2 的方式有多少种。

通过这个方程其实可以推出本题的一些判断条件

• 如果计算出来的 m 是分数的话，那可以直接返回 0，因为题目中给出的全是整数，不可能出现分数的情况
• 如果计算出来的 sum 的绝对值都要小于 target 的话，同样可以直接返回 0，因为不可能凑出结果

因为本题要求的是有多少种方式，所以这里将 dp 数组的含义先定义为有多少种方式，而对于这个方式的限定条件有

• m ：也就是 加法部分 需要达到的和
• 可以选取的数组元素的范围。

if ((target + sum) % 2 != 0) return 0;
if ( target < 0 && sum < -target) return 0;

所以可以将 dp[i][j] 定为在只能选取数组的前 i 个元素的情况下，能够凑成 j 的所有方式有多少种。

那这个状态能否发生转移呢？对于一个新的元素来说，同样会出现两种情况：不选取这个元素，还是按照原来的方式来；另一种就是选取这个元素。但这题与背包问题最大的区别就是 背包问题求得的是最优的情况，而本题求得是有多少种组合，所以背包问题需要求得最大值，而本题则采用 加和 的方式，即
dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]]

💡 这里来说一下数组的第二个部分，也就是 dp[i - 1][j - nums[i]] 的情况，如果现在可以取得 nums[i] 那得到 j 的方式其实就是 dp[i - 1][j - nums[i]] 种，也就是装满 j - nums[i] 有多少种方法，在这个基础上累加一个 nums[i] 也就是 dp[i][j] 要求的情况。

其实本题有个比较特殊的情况，就是当 m 为负数的时候，因为 target 可能为负数，最终导致
m = (target + sum) / 2 也是负数的情况，这时候如果去初始化 dp 数组就会出现下标为负数的情况，所以针对这个情况要做特殊的处理，其实这时候只要将 m 取反，然后去将这个值按照新的 m 去做就可以了，那这个数组就变成了达到 -m 的方式有多少种，这和达到 m 的方式有多少种是完全一样的。

<3> 代码

回溯算法

class Solution {int path = 0;int res = 0;public int findTargetSumWays(int[] nums, int target) {backtracking(nums, target, 0);return res;}public void backtracking(int[] nums, int target, int index) {if (path == target && index == nums.length) {res++;return;}if (index == nums.length) {return;}for (int i = 0; i < 2; i++) {if (i == 0) {path += nums[index];backtracking(nums, target, index + 1);path -= nums[index];} else {path -= nums[index];backtracking(nums, target, index + 1);path += nums[index];}}}
}

动态规划

class Solution {public int findTargetSumWays(int[] nums, int target) {int sum = 0;for (int i : nums) sum += i;if ((target + sum) % 2 != 0) return 0;if ( target < 0 && sum < -target) return 0;int m = (target + sum) / 2; if(m < 0) m = -m; // 处理负值的情况int[] dp = new int[m + 1];                                                                                          dp[0] = 1;for (int i = 0; i < nums.length; i++) {for (int j = m; j >= nums[i]; j--) {dp[j] += dp[j - nums[i]];}}return dp[m];                                         }
}

03. 一和零（No. 474）

题目链接

代码随想录题解

<1> 题目

给你一个二进制字符串数组 strs 和两个整数 m 和 n 。

请你找出并返回 strs 的最大子集的长度，该子集中 最多 有 m 个 0 和 n 个 1 。

如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的 子集 。

示例 1：

输入：strs = [“10”, “0001”, “111001”, “1”, “0”], m = 5, n = 3
输出：4
解释：最多有 5 个 0 和 3 个 1 的最大子集是 {“10”,“0001”,“1”,“0”} ，因此答案是 4 。
其他满足题意但较小的子集包括 {“0001”,“1”} 和 {“10”,“1”,“0”} 。{“111001”} 不满足题意，因为它含 4 个 1 ，大于 n 的值 3 。

示例 2：

输入：strs = [“10”, “0”, “1”], m = 1, n = 1
输出：2
解释：最大的子集是 {“0”, “1”} ，所以答案是 2 。

提示：

• 1 <= strs.length <= 600
• 1 <= strs[i].length <= 100
• strs[i] 仅由 '0' 和 '1' 组成
• 1 <= m, n <= 100

<2> 笔记

本题其实是背包问题的一种变式，将背包问题 背包容量的 一维拓展到了二维；本题中同时限制了两个方向，就是 0 的个数和 1 的个数，所以很简单的思路就是将数组拓展到三维数组，但这样拓展会使得代码编写和理解较为困难，所以想到了使用滚动数组，这样只需要书写二维数组就可以了。

这参考的是 01 背包的滚动数组方法，可以去看一下我的这篇博客：

代码随想录刷题笔记 DAY 42 | 背包问题 - 二维 | 背包问题 - 一维 | 分割等和子集 No.416

因为采用的是滚动数组，所以遍历方向是 从后往前 的

for (int i = m; i >= zero; i--) {for (int j = n; j >= one; j--) {}
}

然后在外层去遍历数组（物品）。

因为题目中求得的是最大子集的长度，所以 dp 数组的定义要尽量往这个方向去靠近，也就是在 n 个字符串中选取得到的子集含有的最多元素数是多少。

dp[i][j] 其实就是要不要加上这个元素，不加上的话就是 dp[i][j] 因为是滚动数组，加上的话就是 dp[i - zero][j - one] + 1 注意这里有两个限制条件。

卡哥最后的总结我非常喜欢，这里来引用一下，我做题的时候确实没有思考到这些：

不少同学刷过这道题，可能没有总结这究竟是什么背包。

此时我们讲解了0-1背包的多种应用，

• 纯 0 - 1 背包 (opens new window)是求 给定背包容量 装满背包 的最大价值是多少。
• 416. 分割等和子集 (opens new window)是求 给定背包容量，能不能装满这个背包。
• 1049. 最后一块石头的重量 II (opens new window)是求 给定背包容量，尽可能装，最多能装多少
• 494. 目标和 (opens new window)是求 给定背包容量，装满背包有多少种方法。
• 本题是求 给定背包容量，装满背包最多有多少个物品。

所以在代码随想录中所列举的题目，都是 0-1背包不同维度上的应用，大家可以细心体会！

<3> 代码

class Solution {public int findMaxForm(String[] strs, int m, int n) {int[][] dp = new int[m + 1][n + 1];for (String s : strs) {int one = getNum(s)[0];int zero = getNum(s)[1];for (int i = m; i >= zero; i--) {for (int j = n; j >= one; j--) {dp[i][j] = Math.max(dp[i][j], dp[i - zero][j - one] + 1);}}}return dp[m][n];}public int[] getNum(String s) {int m = 0;int n = 0;char[] charArray = s.toCharArray();for (char c : charArray) {if ('1' == c) m += 1;else n += 1;}return new int[]{m, n};}
}