一、查看防火墙状态
可通过两种方式查看防火墙状态,一种通过systemctl命令,另一种是通过firewall-cmd命令。
1、systemctl status firewalld
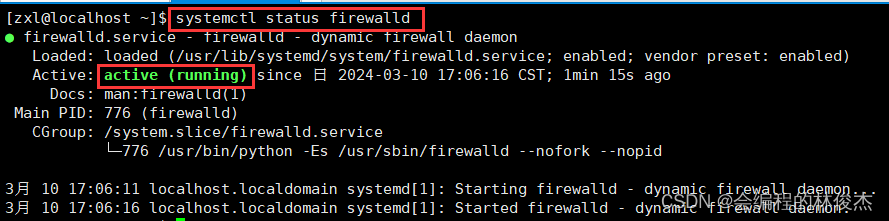
2、firewall-cmd --state
![]()
二、关闭防火墙
1、暂时关闭:设置暂时关闭防火墙将会在下次重启系统后失效
systemctl stop firewalld- 暂时关闭,并查看是否关闭:

- 使用reboot命令重启系统,验证防火墙是否还处于关闭状态:
![]()
通过查看防火墙状态发现,暂时关闭防火墙的方式符合我们之前所说,重启系统之后,防火墙再次被打开。
2、永久关闭:重启系统后才能生效,且重启将不会恢复到原来的状态
systemctl disable firewalld- 永久关闭,并查看是否关闭:

可以看到,该命令执行后并没有立即生效,防火墙仍处于开启状态。
- 使用reboot命令重启系统,验证防火墙是否关闭

系统重启之后,systemctl disable firewalld随即生效,防火墙已被永久关闭。
看到这里,也许大家会产生这样的疑问“为什么永久关闭防火墙需要重启系统才能生效,而暂时关闭则不需要呢?”。下面对此进行一下解答:
在 Linux 系统中,暂时关闭防火墙不需要重启系统是因为防火墙规则是在运行时加载到内存中的,而不是写入到磁盘上。因此,当你暂时关闭防火墙时,只是停止了防火墙服务,并清除了内存中的规则,从而使防火墙失效。这种方式关闭防火墙只在当前会话中有效,一旦系统重启或者重新加载防火墙服务,防火墙规则会重新加载到内存中。
而永久关闭防火墙则需要更改防火墙配置文件(如 iptables、firewalld 的配置文件),这些配置文件会在系统重启时重新加载,并且会将防火墙规则应用到系统启动时的默认配置中。因此,永久关闭防火墙需要重启系统,以便使配置文件的更改生效。
因此,暂时关闭防火墙只会影响当前会话,而永久关闭防火墙则需要修改系统配置文件并重新启动系统才能生效。
三、开启防火墙
开启防火墙同关闭时一样,也分为暂时开启、永久开启,同样的暂时开启只影响当前会话,而永久开启则需要重启系统才能生效,因此这里只做简单的命令演示,不做验证了。
1、暂时开启:当系统重启后将会恢复到原来的状态
systemctl start firewalld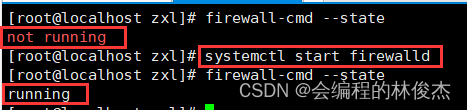
2、永久开启:重启系统后才能生效,且重启将不会恢复到原来的状态
systemctl enable firewalld
重启后,再次查看防火墙状态
![]()
四、firewall-cmd命令
在查看防火墙状态时,我们可以通过firewall-cmd命令来查看;其次,上述我们只介绍了开启、关闭防火墙的的操作,假如我们想在开启防火墙的状态下开放某些端口呢。那么,接下来我再介绍一下firewall-cmd命令,看看它可以为我们提供哪些关于防火墙的操作呢。
firewall-cmd 是用于管理 firewalld 防火墙的命令行工具,它提供了一种简单且强大的方式来配置和管理防火墙规则。
以下是该命令的一些常用操作:
- 查看防火墙状态:firewall-cmd --state
- 重新加载配置:firewall-cmd --reload
- 查看开放的端口:firewall-cmd --list-ports
- 开启防火墙端口:firewall-cmd --zone=public --add-port=端口号/tcp --permanent
命令含义:
–zone #作用域
–add-port=端口号/tcp #添加端口,格式为:端口/通讯协议
–permanent #永久生效,没有此参数重启后失效
注意:添加端口后,必须用命令firewall-cmd --reload重新加载一遍才会生效
- 关闭防火墙端口:firewall-cmd --zone=public --remove-port=端口号/tcp --permanent