python科学计算包中有一个fsolve函数来求解非线性方程组,那么C#中用什么包和什么api与之对应呢?本文仅针对拟牛顿法求解过程展开MathNet包中对应API的考察和测试。
一、案例1
1、方程组
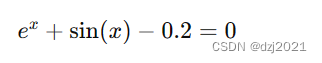
2、python的解法
- (1)代码
from scipy.optimize import fsolve
from math import exp ,sin
def f(x,*arg): f1=exp(x)+sin(x) f2=0.2return(f1-f2)
result=fsolve(f,x0=0)
print(result)
- (2)计算结果:
-0.45173218
- (3) jupyter运行:
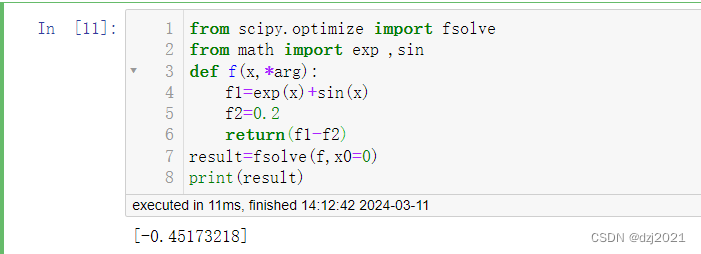
3、C#的解法
- (1)使用的包MathNet
using MathNet.Numerics;
using MathNet.Numerics.RootFinding;
- (2)用——拟牛顿法——Broyden.FindRoot()实现
[ContextMenu("拟牛顿法求根 2 ")]
void testN2()
{// 定义方程组Func<double[], double[]> equations = x => new[] {Math.Exp(x[0]) + Math.Sin(x[0]) - 0.2};try{// 初始猜测double[] initialGuess = { 0.0 };// 使用 Broyden 方法求解方程组double[] solution = Broyden.FindRoot(equations, initialGuess);// 输出解Debug.Log($"方程组的解为: {solution[0]}");}catch (NonConvergenceException ex){Debug.Log($"求解失败: {ex.Message}");}
}
-
(3)计算结果
方程组的解为: -0.451732182380972 -
(4)Win10 + Unity2021.3.18 环境测试
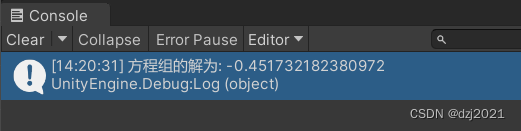
4、结论:
结果一致
二、案例2
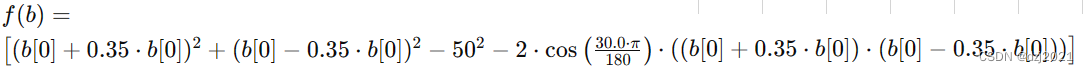
1、Python解法
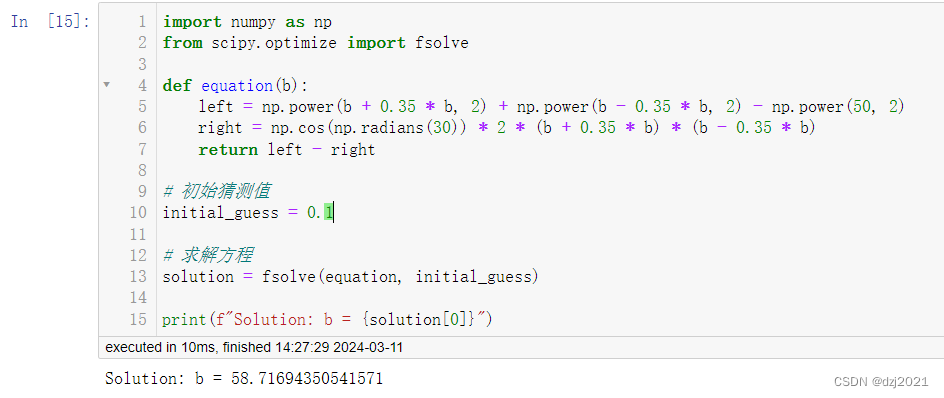
import numpy as np
from scipy.optimize import fsolvedef equation(b):left = np.power(b + 0.35 * b, 2) + np.power(b - 0.35 * b, 2) - np.power(50, 2)right = np.cos(np.radians(30)) * 2 * (b + 0.35 * b) * (b - 0.35 * b)return left - right# 初始猜测值
initial_guess = 0.1# 求解方程
solution = fsolve(equation, initial_guess)print(f"Solution: b = {solution[0]}")
计算结果:
Solution: b = 58.71694350541571
2、C#解法
[ContextMenu("拟牛顿法求根 1 ")]
void testN()
{Func<double[], double[]> equation = b => new[] {Math.Pow(b[0] + 0.35 * b[0], 2) + Math.Pow(b[0] - 0.35 * b[0], 2) - Math.Pow(50, 2) -Math.Cos(30.0 * Math.PI / 180) * 2 * (b[0] + 0.35 * b[0]) * (b[0] - 0.35 * b[0])};double[] initialGuess = { 1 };double[] solution = Broyden.FindRoot(equation, initialGuess,maxIterations:20000);Debug.Log($"方程的解b为: {solution[0]}");
}
结算结果
方程的解b为: 58.7169435054131
3、结论
结果一致
三、案例3
1、方程组
未知数:ϕ0 ,ψ0 ,P0 ,P1 ,P2
方程组:
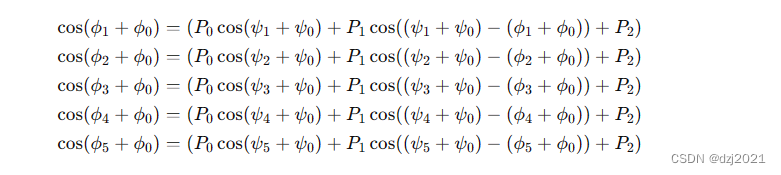
2、 C#的计算过程
// 已知参数double phi1 = 1.46683d.ToRadians(), phi2 = 12.36644d.ToRadians(), phi3 = 30d.ToRadians(), phi4 = 47.63356d.ToRadians(), phi5 = 58.5317d.ToRadians();double psi1 = 3.13922d.ToRadians(), psi2 = 24.33225d.ToRadians(), psi3 = 52.64663d.ToRadians(), psi4 = 75.87842d.ToRadians(), psi5 = 88.40146d.ToRadians(); // 定义方程组函数Func<double[], double[]> equations = x =>{double P0 = x[0];double P1 = x[1];double P2 = x[2];double phi0 = x[3];double psi0 = x[4];double equation1 = Math.Cos(phi1 + phi0) - (P0 * Math.Cos(psi1 + psi0) + P1 * Math.Cos((psi1 + psi0) - (phi1 + phi0)) + P2);double equation2 = Math.Cos(phi2 + phi0) - (P0 * Math.Cos(psi2 + psi0) + P1 * Math.Cos((psi2 + psi0) - (phi2 + phi0)) + P2);double equation3 = Math.Cos(phi3 + phi0) - (P0 * Math.Cos(psi3 + psi0) + P1 * Math.Cos((psi3 + psi0) - (phi3 + phi0)) + P2);double equation4 = Math.Cos(phi4 + phi0) - (P0 * Math.Cos(psi4 + psi0) + P1 * Math.Cos((psi4 + psi0) - (phi4 + phi0)) + P2);double equation5 = Math.Cos(phi5 + phi0) - (P0 * Math.Cos(psi5 + psi0) + P1 * Math.Cos((psi5 + psi0) - (phi5 + phi0)) + P2);return new[] { equation1, equation2, equation3, equation4, equation5 };};// 初始猜测值double[] initialGuess = {20d, 20d, 20d,20d, 20d};// 调用Broyden.FindRoot方法求解double[] solution = Broyden.FindRoot(equations, initialGuess,accuracy:1e-7,maxIterations:10000);// 输出解Debug.Log($"P0 = {solution[0]}, P1 = {solution[1]}, P2 = {solution[2]}, phi0 = {solution[3]}, psi0 = {solution[4]}");
计算结果:

3、结论
与第三方软件的【拟牛顿法】计算结果一致!