T(n) = O（F(n)）

T(n)：Time 渐进时间复杂度

O：正比例关系

F(n)：代码执行次数

只要代码执行的次数越来越多 所耗费的时间也就越来越高

常见的5种：

O(n^2)

O(n logn)

O(n)

O(logn)

O(1):不管重复多少次1次也是这个时间，10次也是这个时间。

时间复杂度排序：由小到大依次：

1.O(1)常数复杂度

2.O(logn)对数复杂度

3.O(n)线性时间复杂度

4.O(n logn)线性对数时间复杂度

5.O(n^2)平方

6.O(n^3)立方

7.O(2^n)指数

8.O(n!)阶乘

以选择排序为例

每次遍历把最小的放到最前面

第二次只要遍历N-1个数，以此类推

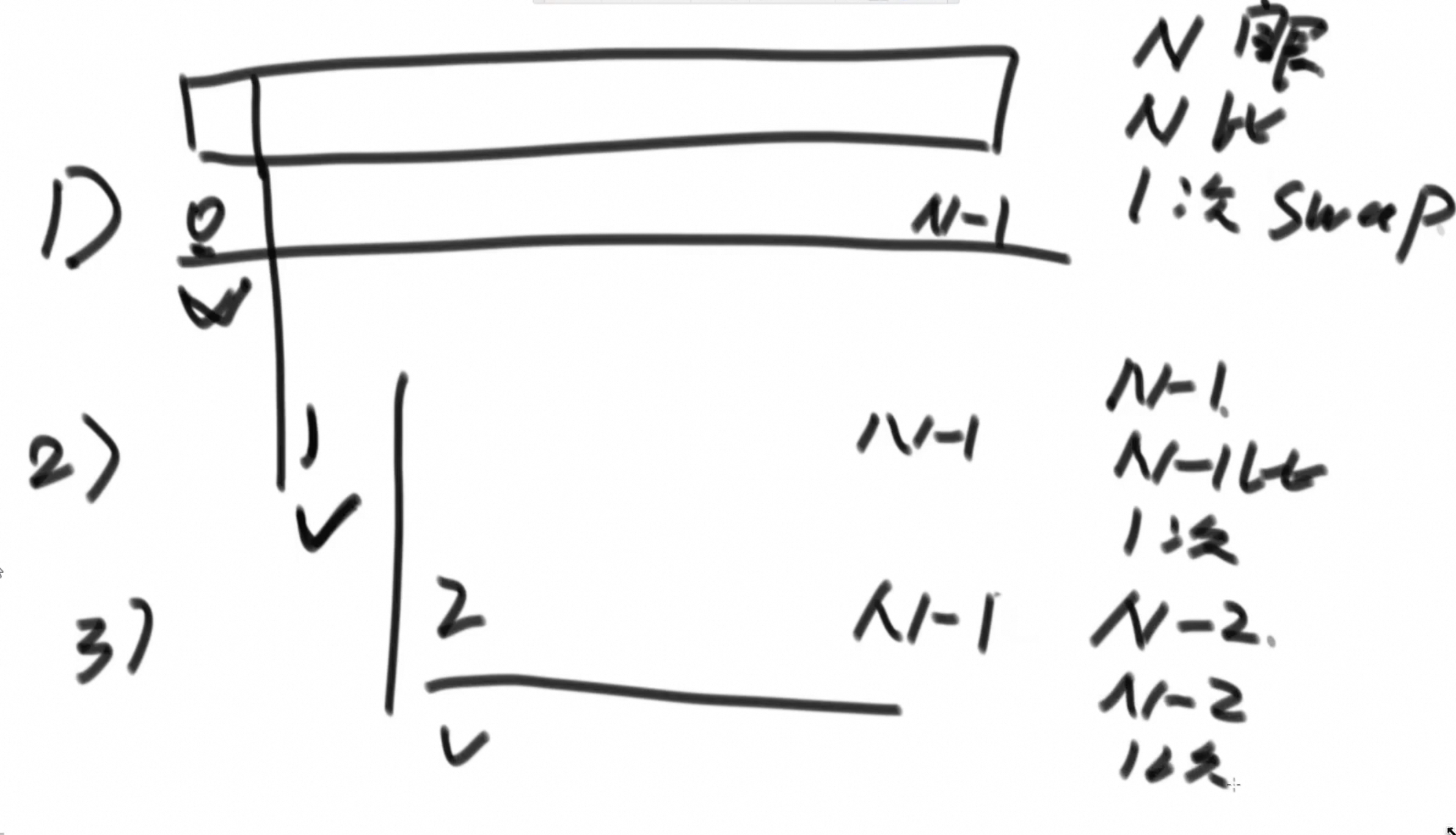
需要看N+N-1+N-2+……+N-N+1眼，

比N+N-1+N-2+……+N-N+1次，

交换N次

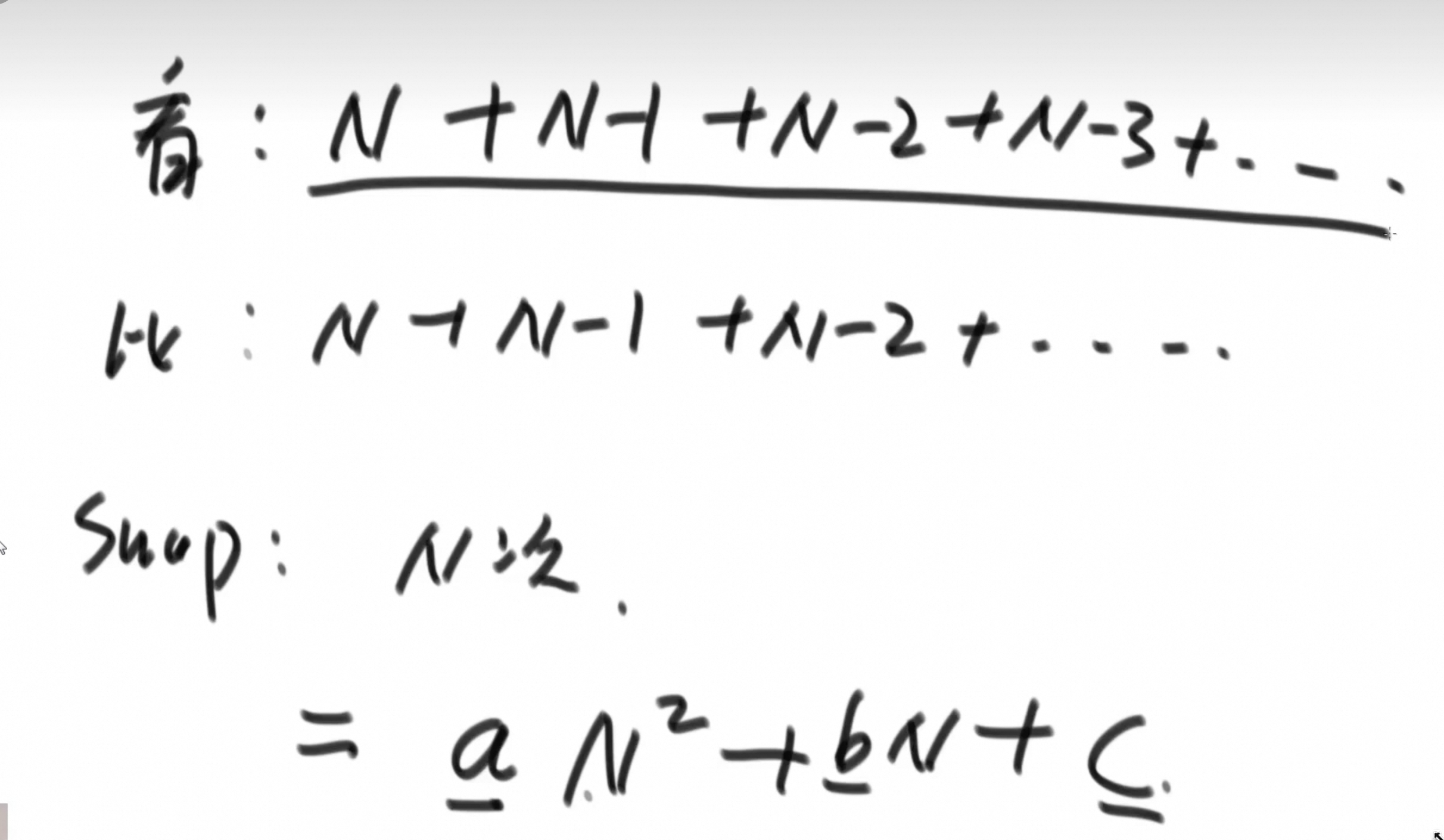
等差数列公式：有n²项

只要高阶项 且忽略高阶项系数得到选择排序算法时间复杂度O(n^2)

当时间复杂度都是同一级别时，只有实际去跑才知道谁更快，因为每个操作加减乘除花的时间无法用理论去估计

ab快速交换的代码【无需额外变量】

前提a和b的内存地址不能一样！！！！ 否则会洗成0 因为自己和自己异或

也就是说数组中 a和b不能是同一个位置

a = a^b;
b = a^b;
a = a^b;

就算 a和b相等 也是能交换成功的

伪代码：

1.O(1)常数复杂度：

①【数组寻址】

②public void m1(){

sout("====hello!");

}