【数据结构】二叉树的层序遍历、前序遍历，中序遍历、后续遍历-编程知识

一、前言

最近也是在准备笔试，由于没有系统的学过数据结构，所以花了半天的时间来学了下二叉树。现在记下来，以便后序查阅。

二、二叉树的遍历概念

二叉树的遍历是指从根结点触发，按照某种次序依次访问二叉树中所有结点，使得每个结点被访问一次且仅被访问一次。

1). 前(先)序遍历

前序遍历：若二叉树为空，则空操作返回，否则先访问根结点，然后前序遍历左子树，再前序遍历右子书。

特点：

根—–>左——->右
根据前序遍历的结果可知第一个访问的必定是root结点

(2). 中序遍历

中序遍历：若二叉树为空，则空操作返回，否则从根结点开始（注意并不是先访问根结点），中序遍历根结点的左子树，然后访问根结点，最后中序遍历右子树。

特点：

左—–>根——->右
根据中序遍历的结果，再结合前序遍历的root结点去划分root结点的左右子树。

(3). 后序遍历

后序遍历：若二叉树为空，则空操作返回，否则从左到右先叶子结点后结点的方式遍历访问左右子树，最后访问根结点。

特点：

左——>右——>根
根据后序遍历的结果可知最后访问的必定是root结点。

(4). 层序遍历

层序遍历：若二叉树为空，则空返回，否则从树的第一层，即根结点开始访问，从上而下逐层遍历，在同一层中，按从左到右的顺序对结点逐个访问。

特点：

从左到右，从上到下
可知第一个访问的必定是root结点

例如：

假如有如下的二叉树：

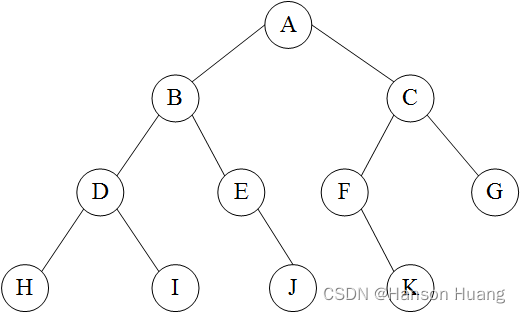
在这里插入图片描述

根据上面的定义，得出如下的遍历结果

前序遍历：ABDHIEJCFKG

中序遍历：HDIBEJAFKCG

后序遍历：HIDJEBKFGCA

层序遍历：ABCDEFGHIJK

我个人根据二叉树图来求遍历结果的经验是：先根据定义，给出所有子树的相对位置，然后再整理。

通过遍历循序确定根的位置，即前序（根在前）、中序（根在中间）、后序（根在最后）

三、根据遍历结果去推其他的遍历结果

相信这种情况下，考题的最多，一是考查如何递归倒推；二是节约试卷版面，画图也麻烦。

1.根据前序遍历、中序遍历，求后序遍历

例：

前序遍历: GDAFEMHZ

中序遍历: ADEFGHMZ

画树求法：

第一步，根据前序遍历的特点，我们知道根结点为G

第二步，观察中序遍历ADEFGHMZ。其中root节点G左侧的ADEF必然是root的左子树，G右侧的HMZ必然是root的右子树。

第三步，观察左子树ADEF，左子树的中的根节点必然是大树的root的leftchild。在前序遍历中，大树的root的leftchild位于root之后，所以左子树的根节点为D。

第四步，同样的道理，root的右子树节点HMZ中的根节点也可以通过前序遍历求得。在前序遍历中，一定是先把root和root的所有左子树节点遍历完之后才会遍历右子树，并且遍历的左子树的第一个节点就是左子树的根节点。同理，遍历的右子树的第一个节点就是右子树的根节点。

第五步，观察发现，上面的过程是递归的。先找到当前树的根节点，然后划分为左子树，右子树，然后进入左子树重复上面的过程，然后进入右子树重复上面的过程。最后就可以还原一棵树了。

该步递归的过程可以简洁表达如下：

确定根,确定左子树，确定右子树。
在左子树中递归。
在右子树中递归。
打印当前根。

那么，我们可以画出这个二叉树的形状：

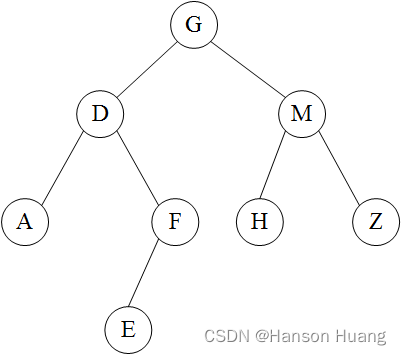
在这里插入图片描述
那么，根据后序的遍历规则，我们可以知道，后序遍历顺序为：AEFDHZMG

2. 已知中序和后序遍历，求前序遍历

依然是上面的题，这次我们只给出中序和后序遍历：

中序遍历: ADEFGHMZ

后序遍历: AEFDHZMG

画树求法：

第一步，根据后序遍历的特点，我们知道后序遍历最后一个结点即为根结点，即根结点为G。

第二步，观察中序遍历ADEFGHMZ。其中root节点G左侧的ADEF必然是root的左子树，G右侧的HMZ必然是root的右子树。

第三步，观察左子树ADEF，左子树的中的根节点必然是大树的root的leftchild。在前序遍历中，大树的root的leftchild位于root之后，所以左子树的根节点为D。

第四步，同样的道理，root的右子树节点HMZ中的根节点也可以通过前序遍历求得。在前后序遍历中，一定是先把root和root的所有左子树节点遍历完之后才会遍历右子树，并且遍历的左子树的第一个节点就是左子树的根节点。同理，遍历的右子树的第一个节点就是右子树的根节点。

第五步，观察发现，上面的过程是递归的。先找到当前树的根节点，然后划分为左子树，右子树，然后进入左子树重复上面的过程，然后进入右子树重复上面的过程。最后就可以还原一棵树了。该步递归的过程可以简洁表达如下：

确定根,确定左子树，确定右子树。
在左子树中递归。
在右子树中递归。
打印当前根。

这样，我们就可以画出二叉树的形状，如上图所示，这里就不再赘述。

那么，前序遍历: GDAFEMHZ

关于二叉树，多练习几次就熟悉了。

四、代码实现

地址：GitHub

import java.util.LinkedList;
import java.util.Queue;/*** 二叉树的前序、中序、后序、层序遍历** @author hanson* @date 2024/3/13 13:56*/
public class Traversal {// 定义树结构static class TreeNode {String val;TreeNode left;TreeNode right;public TreeNode(String val) {this.val = val;this.left = null;this.right = null;}}// 前序遍历 根左右public static void preorderTraversal(TreeNode root) {if (root != null){System.out.println(root.val + " ");preorderTraversal(root.left);preorderTraversal(root.right);}}// 中序遍历 左根右public static void inorderTraversal(TreeNode root) {if (root != null){inorderTraversal(root.left);System.out.println(root.val + " ");inorderTraversal(root.right);}}// 后序遍历 左右根public static void postorderTraversal(TreeNode root) {if (root != null){postorderTraversal(root.left);postorderTraversal(root.right);System.out.println(root.val + " ");}}// 层序遍历public static void levelOrderTraversal(TreeNode root){if (root == null) return;// 我们使用队列来辅助进行二叉树的层序遍历。队列的基本操作有 offer 和 poll：////offer(E e) 方法用于将指定的元素插入到队列中，如果队列满了则返回 false。//poll() 方法用于从队列中取出并删除头部元素，如果队列为空则返回 null。//在二叉树的层序遍历中，我们首先将根节点入队，然后在循环中不断出队并访问节点，同时将其左右子节点入队，直到队列为空为止。这样可以保证按照层次遍历每个节点。Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()){TreeNode node = queue.poll();System.out.println(node.val + " ");if (node.left != null){queue.offer(node.left);}if (node.right != null){queue.offer(node.right);}}}public static void main(String[] args) {// 构造一个二叉树TreeNode root = new TreeNode("A");root.left = new TreeNode("B");root.right = new TreeNode("C");root.left.left = new TreeNode("D");root.left.right = new TreeNode("E");root.right.left = new TreeNode("F");root.right.right = new TreeNode("G");root.left.left.left = new TreeNode("H");root.left.left.right = new TreeNode("I");root.left.right.right = new TreeNode("J");root.right.left.right = new TreeNode("K");// 前序遍历结果：System.out.println("前序遍历结果：");preorderTraversal(root);// 中序遍历结果：System.out.println("中序遍历结果：");inorderTraversal(root);// 后序遍历结果：System.out.println("后序遍历结果：");postorderTraversal(root);// 层序遍历结果：System.out.println("层序遍历结果：");levelOrderTraversal(root);}
}