上一篇中讲了并查集及其原理，在这篇文章中简单应用一下。如果对并查集不是很了解强烈建议先看上一篇。

题目：
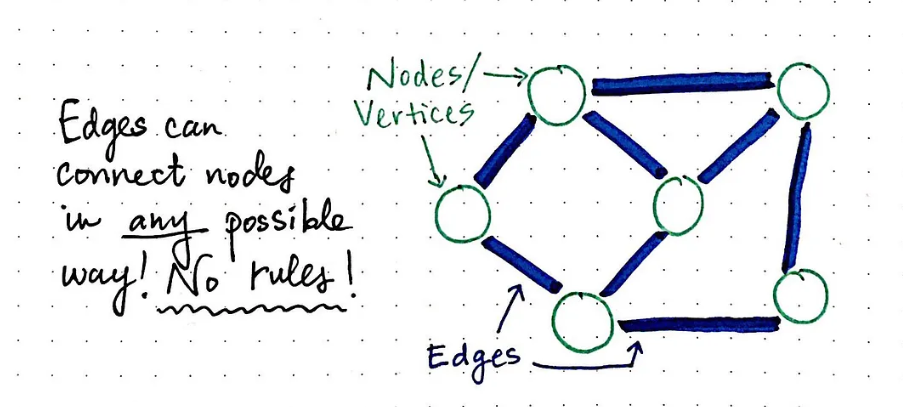
有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。如果isConnected[i][j] = 1，则isConnected[j][i] = 1。

返回矩阵中 省份 的数量。

举例：
根据题目中最后一段所说，给定的n * n矩阵中，如果城市 i 和城市 j相连，则isConnected[i][j] = 1。
如果可以理解为一个2维数组中的行和列，是每个城市之间的连接关系。

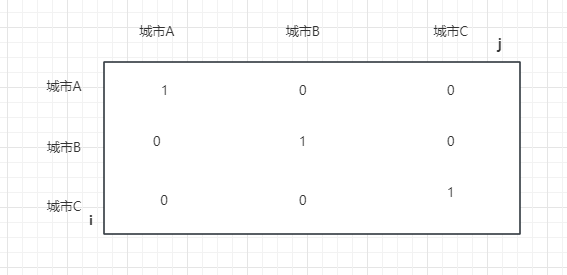
如果所示，i为行数，j为列数。城市A和A本身之间默认是相连的为1，城市A与城市B相连，也为1，A与B相连，B也必定与A相连，所示BA也为1，城市AB之间构成了一大片的省份。城市C与AB都不相连，只有自己，所以CC为1，其余为0，此时图示中省份数为2。

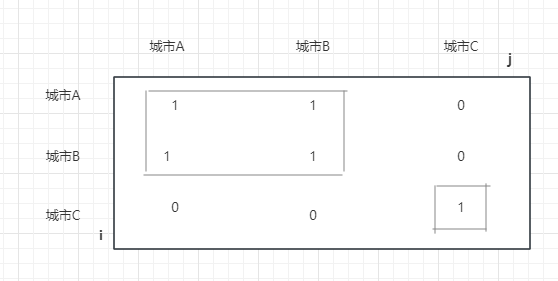
如果ABC之间互不相连，则省份数量为3。

分析：

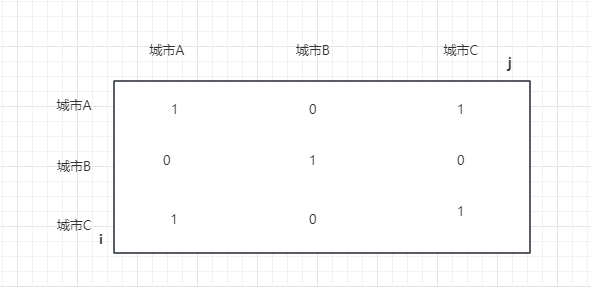
1. 因为isConnected[i][j] = 1，则isConnected[j][i] = 1并且isConnected[i][i] = 1，所以矩阵一定是对称的。所以只需要遍历上半部分就可以（以从左上到右下的对角线为分界）。
2. 以上图为例，AC相连，所以域中有{A,C}，CA与AC域相同，不用管，B与其他两个不相连，单独为域{B}，所以共两个省份{A,C},{B}。
3. 将每个城市看做是一个样本，每个样本是一个独立的集合，如果isConnected[i][i] = 1，则进行合并。合并完后，看一共有几个集合。

实现方式与上一篇中介绍的HashMap方式有所不同，采用数组的形式，常数时间会照比Map更好一些（数组寻址比栈的压栈弹栈快）。

代码实现：

public static int findCircleNum(int[][] M) {int N = M.length;UnionFind unionFind = new UnionFind(N);for (int i = 0; i < N; i++) {for (int j = i + 1; j < N; j++) {if (M[i][j] == 1) {unionFind.union(i, j);}}}return unionFind.sets;}public static class UnionFind {//i位置的parent是parent[i]private int[] parent;//i所在集合大小为size[i]//size[i]是代表节点才有意义，否则无意义private int[] size;//容器，帮助使结构扁平化private int[] help;//集合个数private int sets;public UnionFind(int N) {parent = new int[N];size = new int[N];help = new int[N];sets = N;for (int i = 0; i < N; i++) {parent[i] = i;size[i] = 1;}}//从index开始，找到代表节点，并进行路径压缩public int findParent(int index) {int num = 0;while (index != parent[index]) {help[num++] = index;index = parent[index];}for (int i = 0; i < num; i++) {help[i] = parent[index];}return index;}public boolean isSameSet(int i, int j) {return findParent(i) == findParent(j);}public void union(int i, int j) {int iParent = findParent(i);int jParent = findParent(j);if (iParent != jParent) {if (size[i] >= size[j]){size[i] += size[j];parent[jParent] = iParent;}else{size[j] += size[i];parent[iParent] = jParent;}sets--;}}}