回顾在acw上做过的题

---

 有依赖的背包问题

 

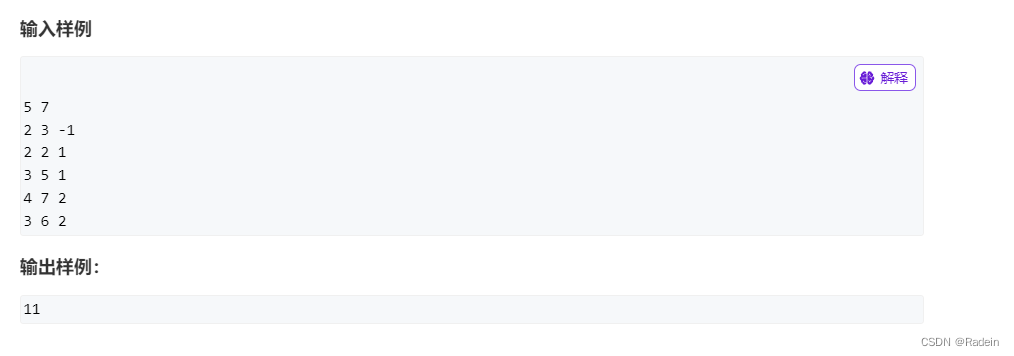
 这一题是与树相关的dp问题，根据父节点与子节点的相连关系，我们用dfs来处理根节点与子树的迭代更新，把每一颗最小单位子树看成一个物品，然后就有点像多重背包（因为有体积限制），又有点像01背包问题（每颗子树要么选要么不选）

f[ i ][ j ] 表示以i为根节点（包含i）的子树，总体积不超过j的最大价值。

然后画一颗dfs深搜树，在回溯的时候进行迭代更新

#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>using namespace std;
const int N = 110;
int v[N],w[N];
vector<int> fa[N];
int f[N][N];
int n,m;void dfs(int x)
{for(int i = v[x]; i <= m; i ++) f[x][i] = w[x];//初始化每个节点在合法体积下的价值for(int i = 0; i < fa[x].size(); i ++){int t = fa[x][i];dfs(t); // dfs找到分支末端for(int j = m; j >= v[x]; j --) //要保证给根节点x赋值，所以体积至少为v[x]for(int k = 0; k <= j - v[x]; k ++) //因为要保证给根节点x赋值，所以给子树分配的体积要留剩下v[x]f[x][j] = max(f[x][j], f[x][j-k]+f[t][k]);}
}int main()
{cin>>n>>m;int root;for(int i = 1; i <= n; i ++){int p;cin>>v[i]>>w[i]>>p;if(p == -1) root = i;elsefa[p].push_back(i);}dfs(root);cout<<f[root][m];
}

背包问题求方案

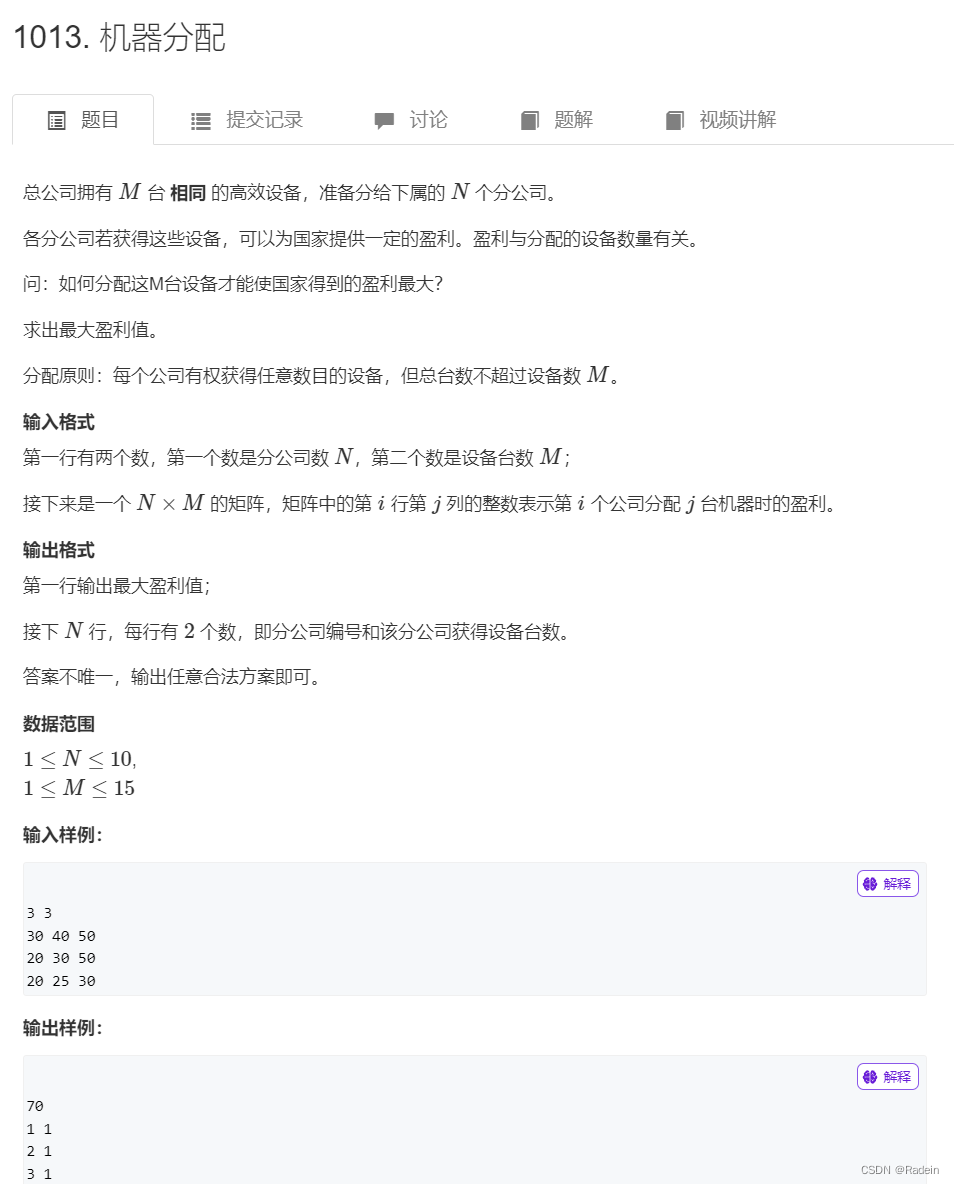
 这道题抽象成多重背包问题。体积就是总共能分配出去多少台机器，k就是枚举给每一家子公司分配出去多少机器，对应的w[ i ][ k ]就是所获得的价值。

接下来就是求方案，这个问题就要思考我们的答案是怎么来的，是通过集合的迭代更新，一步步往后迭代得到f[ n ][ m ]的。那么我们只需要找到这个状态的前一个状态的关系，将他们链接起来，就可以找到具体转移过程中涉及的变量。

#include<iostream>
#include<cstring>
#include<algorithm>using namespace std;
const int N = 11, M = 16;
int f[N][M];
int w[N][M];
int n,m;
int path[N];
int main()
{cin>>n>>m;for(int i = 1; i <= n; i++)for(int j = 1; j <= m; j ++)cin>>w[i][j];//用多重背包的思路来解决for(int i = 1; i <= n; i ++)for(int j = m; j >= 0; j--)for(int k = 0; k <= j; k ++)f[i][j] = max(f[i][j], f[i-1][j-k] + w[i][k]);cout<<f[n][m]<<endl;int j = m;for(int i = n; i >= 1; i--)for(int a = 0; a <= m; a ++){if(f[i-1][j-a] + w[i][a] == f[i][j]) //倒着求，寻找方案{path[i] = a;j -= a;break;}}for(int i = 1; i <= n; i ++) cout<<i<<' '<<path[i]<<endl;
}