题目

输入样例1:
2 2 2
1 2
2 1
输出样例1:
2
输入样例2:
2 3 2
1 2 3
2 1 5
输出样例2:
14思路
题目说从入口开始,只能向右或向下行走到达右下角,类似“摘花生”这道题的模型。题目又说只有当格子里的宝贝价值比小明手中任意宝贝价值都大,小明就可以拿起它,也就说拿到的宝贝价值严格单调递增,是“单调递增子序列”的模型。
状态表示:
那用几维才能表示一个状态呢?首先,需要用 i, j 来表示从起点走到 (i, j) 这个格子的所有路径方案数;然后,需要用ki来表示从起点走到(i, j)这个格子拿了多少个物品;最后,由于拿到的宝贝价值要严格单调递增,因此需要用C表示拿到的最后一个物品的价值。
那为什么我们不用最后一个物品的坐标来表示状态呢,通过坐标也可以得到最后一个物品的价值啊?因为有50 x 50个坐标,并且是这样做会使一个状态表示的维数达到五维,时间复杂度也会增加。题目中取到宝贝的价值有限(0≤Ci≤12),因此可以用C代表最后取到的宝贝的最大值即可,这样可以将维数降到四维。
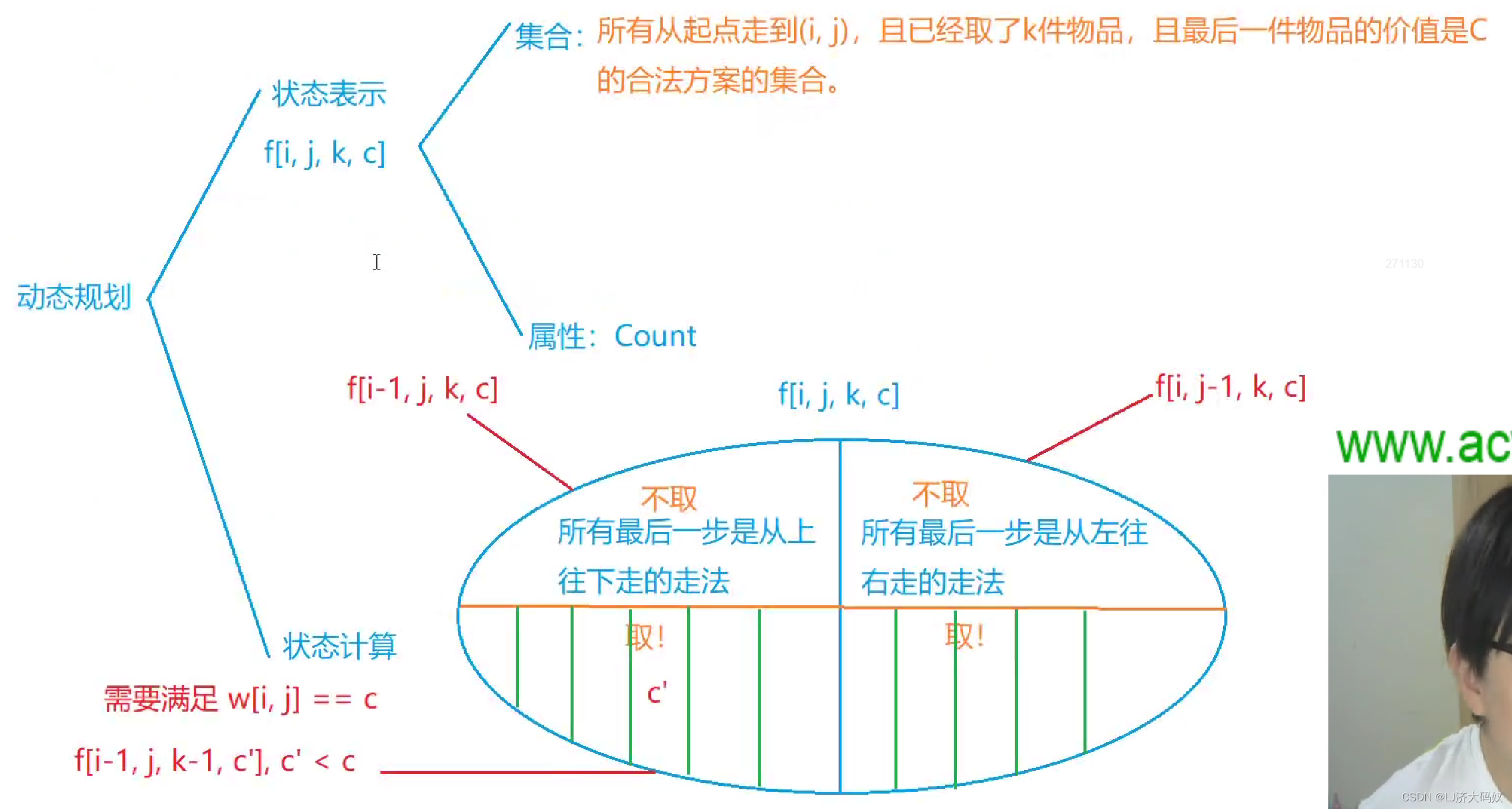
综上所述,我们可以将集合f[i][j][ki][c]定义为所有从起点走到(i,j),且已经取了ki件物品,且最后一件物品的价值是C的合法方案的集合。集合属性为满足集合定义的方案数总和。
状态计算:
由于到达(i, j)这个点只能从左边或上边来,因此可以将集合划分为所有最后一步是从上往下走的走法的集合和所有最后一步是从左往右走的走法的集合。而对于所有最后一步是从上往下走的走法的集合,又可以划分为取不取(i, j)这个格子的宝贝这两个小的集合,当要取(i, j)这个格子的宝贝时,说明这个格子里宝贝价值value比前面拿到的任何宝贝的价值都大,并且,根据集合定义,f[i][j][ki][c]存的是最后一件物品的价值是c的合法方案的集合,因此,当枚举c时,若要取(i, j)这个格子的宝贝还需要满足value等于c。
边界处理
需要注意的是,由于宝贝的价值可能为0,当左上角格子的的宝贝价值为0时,不拿可以表示为f[1][1][0][0] = 1,但下一步(向右或向下走)遇到一个格子的宝贝价值为0,就不能拿了,因为题目要求拿到的宝贝价值要严格单调递增;而实际上,若没有拿左上角格子价值为0的宝贝,在下一步遇到一个价值为0的宝贝是可以选择拿或不拿的。
对此,我们可以将所有格子里宝贝的价值都加上1,宝贝价值区间变成1≤Ci≤13;当c为0时表示还没有拿过任何一件宝贝,“最后一个物品价值为0”。这样处理后,当左上角格子的的宝贝价值为1时,不拿可以表示为f[1][1][0][0] = 1,当下一步(向右或向下走)遇到一个格子的宝贝价值为1,就可以选择拿或不拿了。
int 范围为2.1 x 10^9,因此val最多加两个数就要取模了。
代码
#include<bits/stdc++.h>
using namespace std;
const int MOD = 1000000007, N = 55;
int a[N][N], f[N][N][13][14];
int n, m, k, res;int main()
{cin >> n >> m >> k;for (int i = 1; i <= n; i ++){for (int j = 1; j <= m; j ++){cin >> a[i][j];a[i][j] ++;}}int res = 0;f[1][1][1][a[1][1]] = 1, f[1][1][0][0] = 1;for (int i = 1; i <= n; i ++){for (int j = 1; j <= m; j ++){if (i == 1 && j == 1) continue;for (int ki = 0; ki <= k; ki ++){for (int value = 0; value <= 13; value ++){int &val = f[i][j][ki][value];//不能选(i, j)这个格子里的宝贝//从上往下走,并且不取(i, j)上的宝贝的方案数val = (val + f[i - 1][j][ki][value]) % MOD;//从左往右走,并且不取(i, j)上的宝贝的方案数val = (val + f[i][j - 1][ki][value]) % MOD;if (ki > 0 && value == a[i][j]){for (int c = 0; c < value; c ++){//从前面的状态中选价值c < value并且选了ki - 1件的fval = (val + f[i - 1][j][ki - 1][c]) % MOD;val = (val + f[i][j - 1][ki - 1][c]) % MOD;}}}}}}for (int i = 1; i <= 13; i ++) res = (res + f[n][m][k][i]) % MOD;cout << res;return 0;
}
感觉DP就是根据集合定义打好表,算出全部的状态的值,然后查询表中符合题目要求的状态值。