C++进阶--红黑树

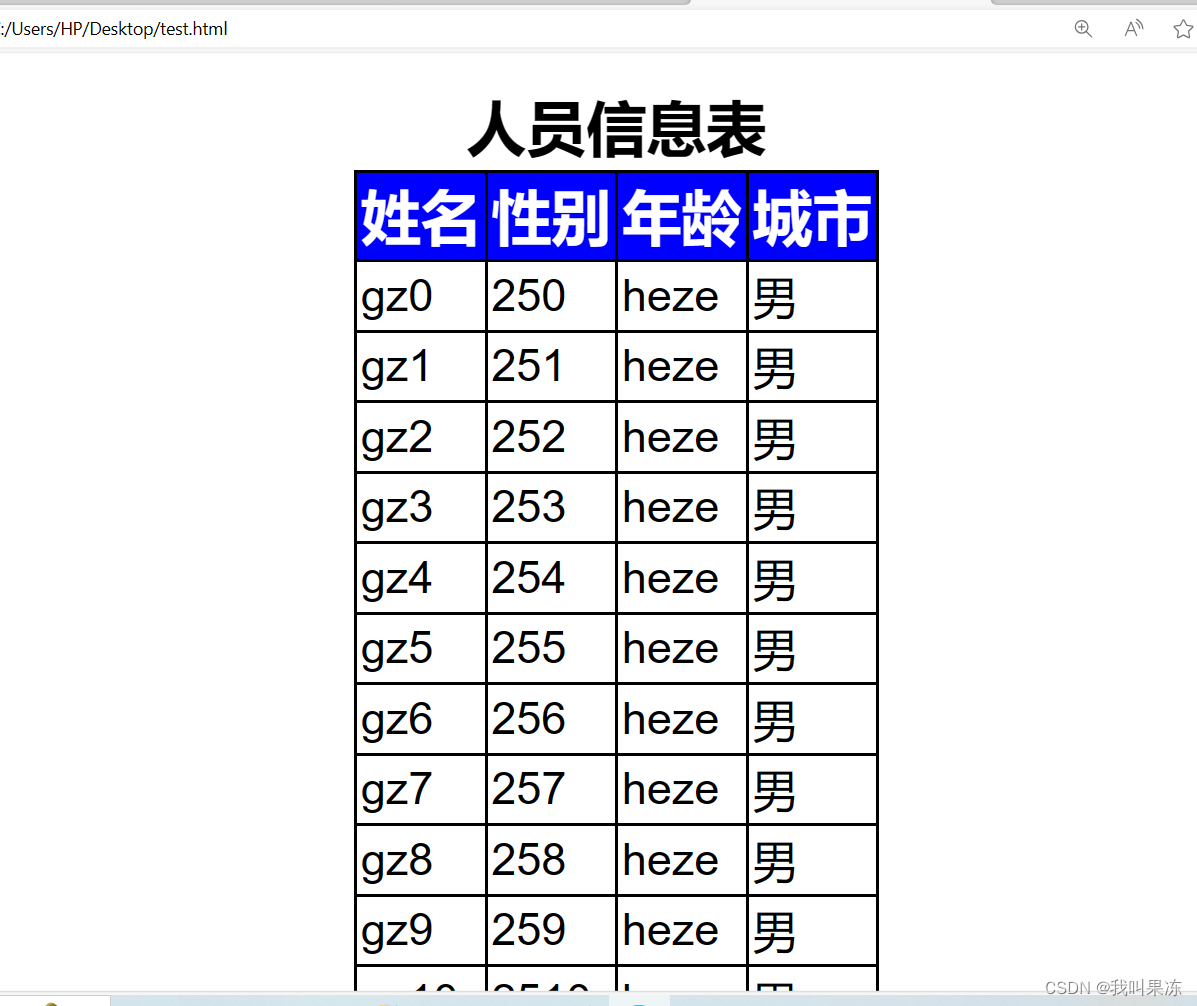
概念与特性

红黑树，是一种自平衡的二叉搜索树，它具有以下特点：

  1. 每个节点要么是红色，要么是黑色
  2. 根节点是黑色的。
  3. 每个叶子节点（NIL节点，空节点）都是黑色的。
  4. 如果一个节点是红色的，那么它的两个子节点都是黑色的，也就说，不存在两个连续的红色节点。
  5. 对于任意节点，从该节点到其后代叶子节点的所有路径上包含相同数目的黑色节点，即保证了红黑树的黑色节点高度相同。

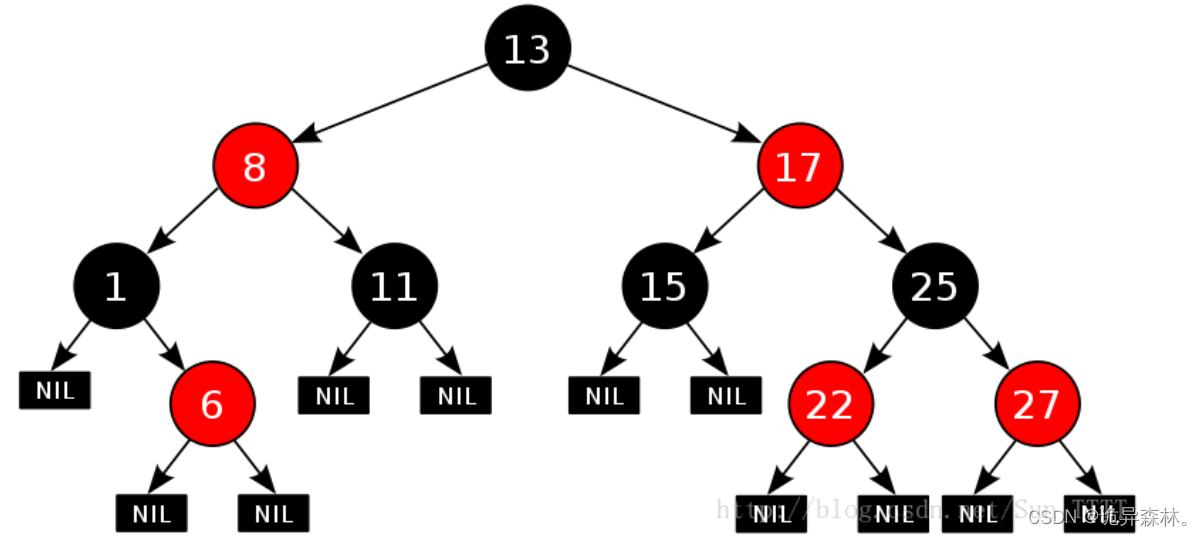
在这里插入图片描述

红黑树的定义

enum Colour
{RED,BLACK
};template<class K,class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col;RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED){}
};

在这里插入图片描述

红黑树的插入操作

旋转的见：AVL树链接入口

bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}//确定插入位置Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}//确定cur节点和p节点的位置关系cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;//情况一if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//向上处理cur = grandfather;parent = cur->_parent;}else//情况2{if (cur == parent->_left){//      g//    p    u//  cRotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//      g//    p    u//      cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;//旋转完的子树的根节点必为黑，这时就不用向上调整处理了}}else{Node* uncle = grandfather->_left;// 情况一：叔叔存在且为红if (uncle && uncle->_col == RED){// 变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续往上处理cur = grandfather;parent = cur->_parent;}else//情况2{if (cur == parent->_right){//      g//    u    p//           cRotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//      g//    u    p//        cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;//旋转完的子树的根节点必为黑，这时就不用向上调整处理了}}}_root->_col = BLACK;return true;}

在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

验证

void TestRBTree1()
{int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };RBTree<int, int> t;for (auto e : a){t.Insert(make_pair(e, e));}t.InOrder();cout << t.IsBalance() << endl;
}

在这里插入图片描述
在这里插入图片描述

bool Check(Node* cur, int blackNum, int refBlackNum){if (cur == nullptr){//当节点为空时，表示这条路径结束，这时就要对黑色节点进行判断if (refBlackNum != blackNum){cout << "与其他路径的黑色节点数不相等" << endl;return false;}return true;}if (cur->_col == RED && cur->_parent->_col == RED){cout << cur->_kv.first << "存在连续的红色节点" << endl;return false;}if (cur->_col == BLACK){blackNum++;}return Check(cur->_left,blackNum,refBlackNum) && Check(cur->_right,blackNum,refBlackNum);}bool IsBalance(){if (_root && _root->_col == RED)return false;//统计一条路径的黑色节点数int refBlackNum = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK){refBlackNum++;}cur = cur->_left;}return Check(_root,0,refBlackNum);}

在这里插入图片描述

红黑树的性能测试

void TestRBTree2()
{const int N = 1000000;vector<int> v;v.reserve(N);srand(time(0));for (size_t i = 0; i < N; i++){v.push_back(rand() + i);}//测插入所需时间size_t begin2 = clock();RBTree<int, int> t;for (auto a : v){t.Insert(make_pair(a, a));}size_t end2 = clock();cout << "Insert:" << end2 - begin2 << endl;cout << t.IsBalance() << endl;//测高度，数量cout << "height" << t.Height() << endl;cout << "Size:" << t.Size() << endl;//测查找时间size_t begin1 = clock();for (size_t i = 0; i < N; i++){t.Find((rand() + i));}size_t end1 = clock();cout << "Find:" << end1 - begin1 << endl;}

在这里插入图片描述

原码

#pragma once
enum Colour
{RED,BLACK
};template<class K,class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col;RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED){}};template<class K,class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}//确定插入位置Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}//确定cur节点和p节点的位置关系cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;//情况一if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//向上处理cur = grandfather;parent = cur->_parent;}else//情况2{if (cur == parent->_left){//      g//    p    u//  cRotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//      g//    p    u//      cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;//旋转完的子树的根节点必为黑，这时就不用向上调整处理了}}else{Node* uncle = grandfather->_left;// 情况一：叔叔存在且为红if (uncle && uncle->_col == RED){// 变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续往上处理cur = grandfather;parent = cur->_parent;}else//情况2{if (cur == parent->_right){//      g//    u    p//           cRotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//      g//    u    p//        cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;//旋转完的子树的根节点必为黑，这时就不用向上调整处理了}}}_root->_col = BLACK;return true;}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;subR->_left = parent;Node* ppnode = parent->_parent;parent->_parent = subR;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subR;}else{ppnode->_right = subR;}subR->_parent = ppnode;}}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;Node* ppnode = parent->_parent;parent->_parent = subL;if (parent == _root){_root = subL;subL->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subL;}else{ppnode->_right = subL;}subL->_parent = ppnode;}}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << endl;_InOrder(root->_right);}void InOrder(){_InOrder(_root);}bool Check(Node* cur, int blackNum, int refBlackNum){if (cur == nullptr){//当节点为空时，表示这条路径结束，这时就要对黑色节点进行判断if (refBlackNum != blackNum){cout << "与其他路径的黑色节点数不相等" << endl;return false;}return true;}if (cur->_col == RED && cur->_parent->_col == RED){cout << cur->_kv.first << "存在连续的红色节点" << endl;return false;}if (cur->_col == BLACK){blackNum++;}return Check(cur->_left,blackNum,refBlackNum) && Check(cur->_right,blackNum,refBlackNum);}bool IsBalance(){if (_root && _root->_col == RED)return false;//统计一条路径的黑色节点数int refBlackNum = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK){refBlackNum++;}cur = cur->_left;}return Check(_root,0,refBlackNum);}size_t Size(){return _Size(_root);}size_t _Size(Node* root){if (root == NULL)return 0;return _Size(root->_left)+ _Size(root->_right) + 1;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_kv.first < key){cur = cur->_right;}else if (cur->_kv.first > key){cur = cur->_left;}else{return cur;}}return NULL;}int _Height(Node* root){if (root == nullptr)return 0;int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}int Height(){return _Height(_root);}private:Node* _root = nullptr;
};void TestRBTree1()
{int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };RBTree<int, int> t;for (auto e : a){t.Insert(make_pair(e, e));}t.InOrder();cout << t.IsBalance() << endl;
}//性能测试
void TestRBTree2()
{const int N = 1000000;vector<int> v;v.reserve(N);srand(time(0));for (size_t i = 0; i < N; i++){v.push_back(rand() + i);}//测插入所需时间size_t begin2 = clock();RBTree<int, int> t;for (auto a : v){t.Insert(make_pair(a, a));}size_t end2 = clock();cout << "Insert:" << end2 - begin2 << endl;cout << t.IsBalance() << endl;//测高度，数量cout << "height" << t.Height() << endl;cout << "Size:" << t.Size() << endl;//测查找时间size_t begin1 = clock();for (size_t i = 0; i < N; i++){t.Find((rand() + i));}size_t end1 = clock();cout << "Find:" << end1 - begin1 << endl;}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/537210.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

Python 查找PDF中的指定文本并高亮显示

Python 查找PDF中的指定文本并高亮显示

在处理大量PDF文档时&#xff0c;有时我们需要快速找到特定的文本信息。本文将提供以下三个Python示例来帮助你在PDF文件中快速查找并高亮指定的文本。 查找并高亮PDF中所有的指定文本查找并高亮PDF某个区域内的指定文本使用正则表达式搜索指定文本并高亮 本文将用到国产第三方…
阅读更多...
mac启动skywalking报错

mac启动skywalking报错

这个命令显示已经成功 但是日志报错了以上内容。 然后去修改。vim .bash_profile 查看全局变量&#xff0c;这个jdk却是有2个。所以这个问题没解决。
阅读更多...
设计模式 — — 单例模式

设计模式 — — 单例模式

一、是什么 单例模式只会在全局作用域下创建一次实例对象&#xff0c;让所有需要调用的地方都共享这一单例对象 二、实现 // 单例构造函数 function CreateSingleton (name) {this.name name;this.getName(); };// 获取实例的名字 CreateSingleton.prototype.getName func…
阅读更多...
【高效开发工具系列】Java读取Html

【高效开发工具系列】Java读取Html

&#x1f49d;&#x1f49d;&#x1f49d;欢迎来到我的博客&#xff0c;很高兴能够在这里和您见面&#xff01;希望您在这里可以感受到一份轻松愉快的氛围&#xff0c;不仅可以获得有趣的内容和知识&#xff0c;也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…
阅读更多...
Ubuntu 14.04：安装 PaddleOCR 2.3

Ubuntu 14.04：安装 PaddleOCR 2.3

目录 一、说明 1.1 如何选择版本 1.2 查看 github 中的 PaddleOCR 版本 二、安装 2.1 安装前环境准备 2.2 下载包 2.3 解压 2.4 安装依赖库 异常处理&#xff1a;Read timed out. 2.5 下载推理模型&#xff1a;inference 2.5.1 模型存放位置 2.5.2 模型下载链接 2.5.…
阅读更多...
es 聚合操作（一）

es 聚合操作（一）

前言 Elasticsearch除搜索以外&#xff0c;提供了针对ES 数据进行统计分析的功能。聚合(aggregations)可以让我们极其方便的实现对数据的统计、分析、运算。例如&#xff1a; 衣服品牌的受欢迎程度这些衣服的平均价格、最高价格、最低价格这些衣服的每天、每月销量如何 使用…
阅读更多...
Rust 构建开源 Pingora 框架可以与nginx媲美

Rust 构建开源 Pingora 框架可以与nginx媲美

一、概述 Cloudflare 为何弃用 Nginx&#xff0c;选择使用 Rust 重新构建新的代理 Pingora 框架。Cloudflare 成立于2010年&#xff0c;是一家领先的云服务提供商&#xff0c;专注于内容分发网络&#xff08;CDN&#xff09;和分布式域名解析。它提供一系列安全和性能优化服务…
阅读更多...
xcode15，个推推送SDK闪退问题处理办法

xcode15，个推推送SDK闪退问题处理办法

个推iOS推送SDK最新版本 优化了xcode15部分场景下崩溃问题&#xff0c;以及回执上传问题&#xff0c;近期您的应用有发版计划&#xff0c;建议更新SDK&#xff1a; 1&#xff09;GTSDK更新到3.0.5.0以及以上版本&#xff1b; 2&#xff09;GTCommonSDK更新到3.1.0.0及以上版本…
阅读更多...
【深度学习目标检测】二十三、基于深度学习的行人检测计数系统-含数据集、GUI和源码（python，yolov8）

【深度学习目标检测】二十三、基于深度学习的行人检测计数系统-含数据集、GUI和源码（python，yolov8）

行人检测计数系统是一种重要的智能交通监控系统&#xff0c;它能够通过图像处理技术对行人进行实时检测、跟踪和计数&#xff0c;为城市交通规划、人流控制和安全管理提供重要数据支持。本系统基于先进的YOLOv8目标检测算法和PyQt5图形界面框架开发&#xff0c;具有高效、准确、…
阅读更多...
Linux 网络套接字编程基础

Linux 网络套接字编程基础

端口号 我们在上一篇文章中以打电话的例子得出结论&#xff1a;在进行网络通信的时候&#xff0c;不是我们的两台机器在进行通信&#xff0c;本质上是应用层在进行通信。 为什么这么说呢&#xff1f; 网络协议的下三层&#xff0c;解决的是数据安全可靠地发送到远端机器。这…
阅读更多...
BUU [FBCTF2019]RCEService

BUU [FBCTF2019]RCEService

BUU [FBCTF2019]RCEService 开题&#xff0c;要求以json格式输入命令。 无任何信息泄露&#xff0c;源码如下&#xff1a; <?phpputenv(PATH/home/rceservice/jail);if (isset($_REQUEST[cmd])) {$json $_REQUEST[cmd];if (!is_string($json)) {echo Hacking attempt de…
阅读更多...
开源导出html表格项目-easyHtml

开源导出html表格项目-easyHtml

开源导出html表格项目-easyHtml 背景介绍 背景 项目的由来&#xff0c;在面试的过程中&#xff0c;发现这个需求&#xff08;导出html表格&#xff09;比较常见&#xff0c;同时也引起我的兴趣&#xff0c;所以就有了开源项目easyHtml第一个版本 介绍 功能 支持自定义表格标…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023