【C++ 】stack 和 queue-编程知识

【C++ 】stack 和 queue

1. 标准库中的stack

stack 的介绍：

1. stack是一种容器适配器，专门用在具有后进先出操作的上下文环境中，其删除只能从容器的一端进行元素的插入与提取操作

2. stack是作为容器适配器被实现的，容器适配器即是对特定类封装作为其底层的容器，并提供一组特定的成员函数来访问其元素，将特定类作为其底层的，元素特定容器的尾部(即栈顶)被压入和弹出

3. stack的底层容器可以是任何标准的容器类模板或者一些其他特定的容器类

a. stack 的使用

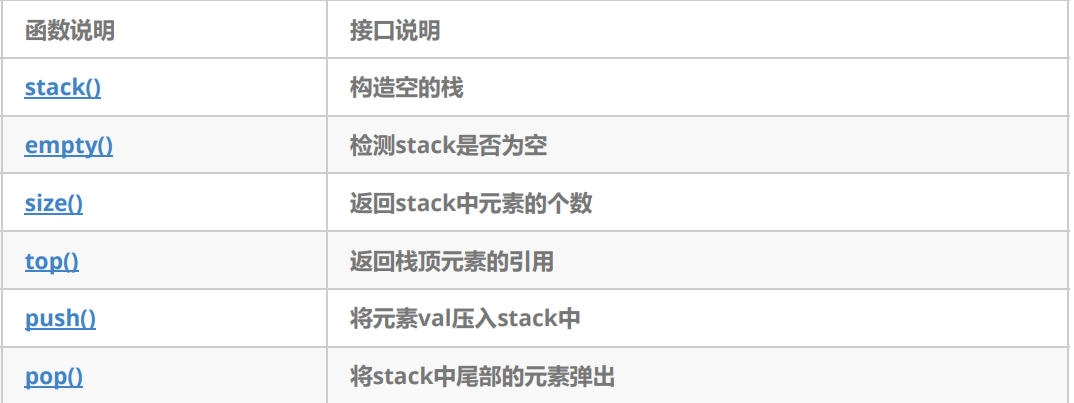
注意：

如果要访问所有元素得到栈顶元素，再pop，直到为空

2. stack的模拟实现

代码

namespace lhy
{ template<class T,class container = vector<T>>class stack{public:void push(const T& x){_t.push_back(x);}void pop(){_t.pop_back();}size_t size(){return _t.size();}bool empty(){return _t.empty();}const T& top(){return _t.back();}private:container _t;};

//用法很像缺省参数，不过这里缺省的是类型

3. 标准库中的queue

queue 的介绍：

1. 队列是一种容器适配器，专门用于在FIFO上下文(先进先出)中操作，其中从容器一端插入元素，另一端提取元素

2. 队列作为容器适配器实现，容器适配器即将特定容器类封装作为其底层容器类，queue提供一组特定的成员函数来访问其元素。元素从队尾入队列，从队头出队列

3. 底层容器可以是标准容器类模板之一，也可以是其他专门设计的容器类

a. queue 的使用

4. queue的模拟实现

代码

namespace lhy
{ template<class T,class container = list<T>>class queue{public:void push(const T& x){_v.push_back(x);}void pop(){_v.pop_front();}bool empty(){return _v.size() == 0;}const T& back(){return _v.back();}const T& front(){return _v.front();}size_t size(){return _v.size();}private:container _v;};

5. priority_queue （优先级队列）

优先级队列的介绍：

优先级队列默认使用vector作为其底层存储数据的容器，在vector上又使用了堆算法将vector中元素构造成堆的结构

因此priority_queue就是堆，所有需要用到堆的位置，都可以考虑使用priority_queue

注意：

默认情况下priority_queue是大堆

a. priority_queue 的使用

priority_queue() (无参构造函数)
priority_queue(InputIterator first, InputIterator last)
empty() (判空)
push() (尾插)
pop () （删除栈顶元素，即第一个元素）
top() (返回栈顶元素)

6. priority_queue 的模拟实现

代码

namespace lhy
{template<class T>struct less{bool operator()(const T& x, const T& y){return x > y;}};template<class T>struct greater{bool operator()(const T& x, const T& y){return x < y;}};template<class T, class container = vector<T>, class compare = less<T>>class priority_queue{private:container con;void AdjustUp(int child){int parent = (child - 1) / 2;while (child > 0){if (compare()(con[parent], con[child])){std::swap(con[parent], con[child]);}else{break;}child = parent;parent = (child - 1) / 2;}}void AdjustDown(int parent){int child = parent * 2 + 1;while (child < size()){if (child + 1 < size() && con[child] > con[child + 1]){child++;}if (compare()(con[parent], con[child])){std::swap(con[parent], con[child]);}else{break;}parent = child;child = parent * 2 + 1;}}public:size_t size(){return con.size();}void push(const T & x){con.push_back(x);AdjustUp(size() - 1);}void pop(){swap(con[0], con[size() - 1]);con.pop_back();AdjustDown(0);}bool empty(){return con.empty();}const T& top(){return con[0];}};
}