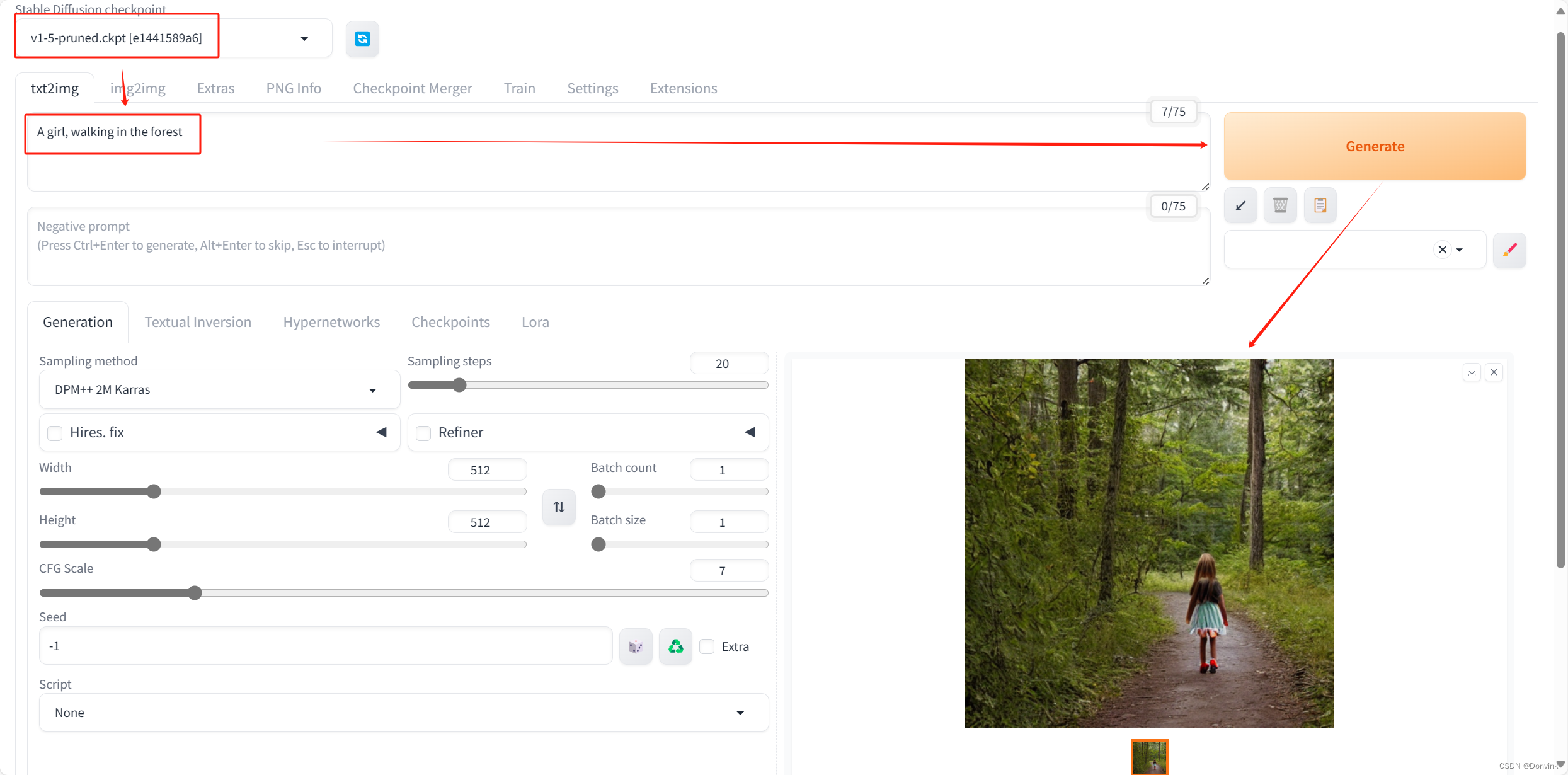
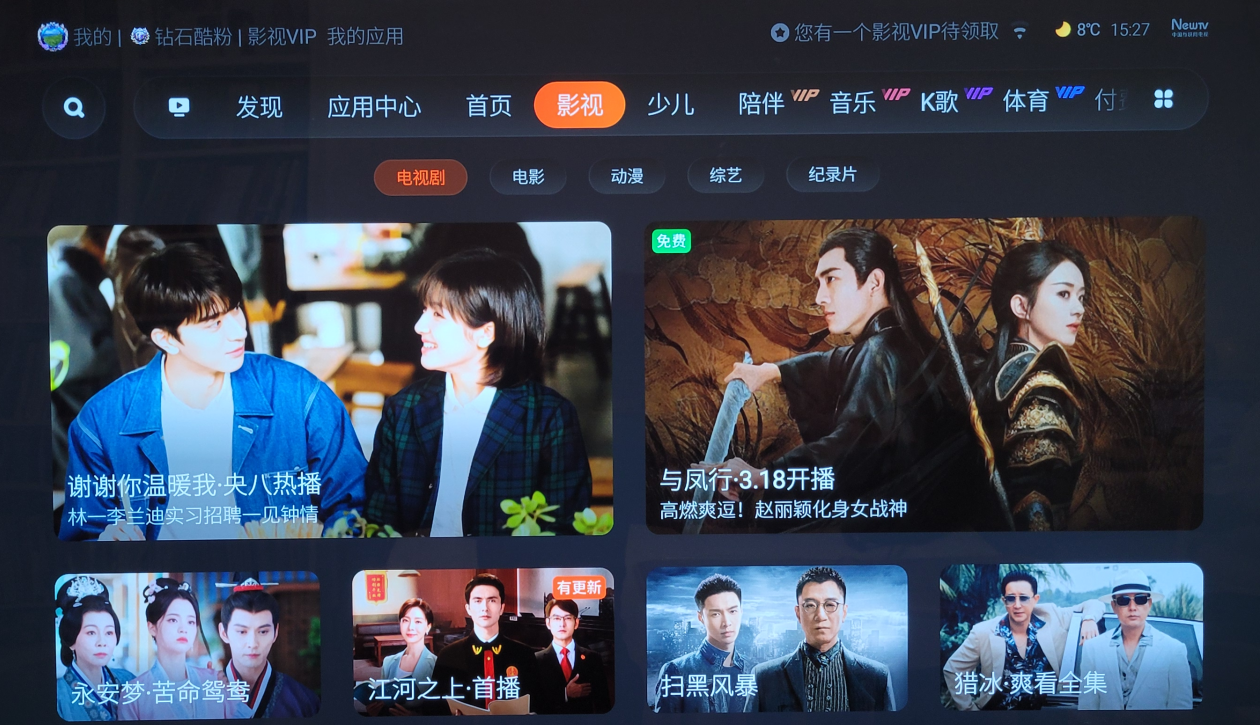
搜索:暴力法算法思想的具体实现
搜索:通用的方法,一个问题如果比较难,那么先尝试一下搜索,或许能启发出更好的算法
技巧:竞赛时遇到不会的难题,用搜索提交一下,说不定部分判题数据很弱,得分了
暴力法
把所有的可能性都列举出来,一一验证,简单直接
利用计算机强大的计算能力和存储能力
依赖的是递归
深度优先搜索
Depth First Search 即 DFS,意为深度优先搜索,是所有的搜索手段之一。它是从某个状态开始,不断进行状态转移,直到不能转移后,向后回退,一直到遍历完所有的状态。
深度优先搜索基本概念
作为搜索算法的一种,DFS 主要是用于解决 NP 完全问题。但是,深度优先搜索算法的时间复杂度较高,深度优先搜索是 O ( n ! ) O(n!) O(n!) 的阶乘级算法,它的效率非常低,在数据规模变大时,此算法就难以解决当前的问题了。
所以搜索算法使用于状态节点较小规模的问题。
DFS 的设计步骤
按照定义设计:
- 确定该题目的状态(包括边界)
- 找到状态转移方式
- 找到问题的出口,计数或者某个状态
- 设计搜索
DFS基础:递归和记忆化搜索
形式上,递归函数是自己调用自己,是一个不断重复的过程
递归的思想是把大问题逐步缩小,直到变成最小的同类问题的过程,而最后的小问题的解是已知的,一般是给定的初始条件
到达最小问题之后,再回溯,把小问题的解逐个带回给更大的问题,最终大问题也得到了解决
递归有两个过程:递归前进、递归返回
在递归过程中,由于大问题和小问题的解决方法完全一样,那么大问题的代码和小问题的代码可以写成一样
一个递归函数,直接调用自己,实现了程序的复用
DFS的代码框架
ans //答案,用全局变量表示
def dfs (层数 (状态), 其他参数):if (条件判断) //到达最底层(达到最终状态),或者满足条件退出更新答案 //答案一般用全局变量表示return //返回到上一层剪枝 //在进一步DFS之前剪枝for (枚举下一层可能的情况)://对每一个情况继续DFSif (used[i] == 0): //如果状态i没有用过,就可以进入下一层used[i] = 1 //称为保存现场,占有现场//标记状态i,表示已经用过,在更底层不能再使用dfs(层数+1, 其他参数) //下一层used[i] = 0 //称为恢复现场,释放现场//恢复状态,回溯时,不影响上一层对这个状态的使用return //返回到上一层
剪枝
题目中给了要求是y<30
当扩展到y=29这个点以后,就不需要继续往后扩展了
伪代码:
int check(参数)
{if(满足条件)return 1;return 0;
}
bool pd(参数){相应操作
}
void dfs(int step)
{判断边界pd(){不在边界内,即回溯}尝试每一种可能{满足check条件标记继续下一步dfs(step+1)恢复初始状态(回溯的时候要用到)}
}
DFS:剪枝
剪枝:把不会产生答案的,或不必要的枝条剪掉
剪枝的关键:剪什么枝、在哪里剪
剪枝是搜索常用的优化手段,常常能把指数级的复杂度,优化到近似多项式的复杂度
可行性剪枝:对当前状态进行检查,如果当前条件不合法就不再继续,直接返回
搜索顺序剪枝:搜索树有多个层次和分支,不同的搜索顺序会产生不同的搜索树形态
最优性剪枝:在最优化问题的搜索过程中,如果当前花费的代价已超过前面搜索到的最优解,那么本次搜索已经没有继续进行下去的意义,停止对当前分支的搜索
排除等效冗余:搜索不同的分支,最后的结果是一样的,那么只搜一个分支就够了
记忆化搜索:在递归的过程中,有许多分支被反复计算,会大大降低算法执行的效率。将已经计算出来的结果保存起来,以后需要用到的时候直接取出结果,避免重复运算,从而提高了算法的效率
DFS 题目讲解
1. 状态搜索代表: N 皇后问题
题目链接
难度: 简单
标签: DFS
题目描述:
在N×N的方格棋盘放置了N 个皇后,使得它们不相互攻击(即任意 22 个皇后不允许处在同一排,同一列,也不允许处在与棋盘边框成 45 角的斜线上。你的任务是,对于给定的N,求出有多少种合法的放置方法。
输入描述:
输入中有一个正整数 N≤10,表示棋盘和皇后的数量
输出描述:
为一个正整数,表示对应输入行的皇后的不同放置数量。
输入输出样例:
示例:
输入:
5
输出:
10
运行限制:
最大运行时间:1s最大运行内存: 256M
解题思路:
二维搜索问题,有一个x坐标一个y坐标
下面是用递归的深度优先搜索求解 n 皇后问题的算法描述:
这里用一个 N×N 的矩阵来表示棋盘,但是我们不需要定义这样的数组,只要心中有 N×N 的棋盘即可。
- 算法开始:
当前行设为第一行,当前列设为第一列,从第一行第一列开始搜索,即只能让皇后从第一行放到第 n 行。
这样在每次判断是否满足情况时我们不用去判断是否皇后在相同行。
我们只用判断之前的 1 到 a−1 个皇后的位置和当前第 a 个皇后的位置是否属于同一列或者斜线,判断是否同一列。 - 判断边界:
在当前行,当前列的位置上判断是否满足条件(即保证经过这一点的行,列与斜线上都没有两个皇后),若不满足,跳到第 5 步,即不符合边界条件。
首先说一下,什么叫不符合边界条件,不只是跳出了搜索范围,剪枝也可以从这里开始,比如这里不满足条件,向下继续搜索也不会再有结果。
这可以理解为超出边界的剪枝,我们的边界只得可能存在解的范围,这里已经超出有解的范围,必然要被踢出。
判断条件:
我们用数组 x [ a ] = i x[a]=i x[a]=i 来表示第 a 个皇后的位置在第 a 行第 i 列,我们不用考虑是否在同一行的问题你,我们只用判断之前的 1 到 a−1 个皇后的位置和当前第 a 个皇后的位置是否属于同一列或者斜线。
判断是否属于同一列: 就判断 x [ a ] x[a] x[a] 是否等于 x [ i ] x[i] x[i]; 判断是否属于同一斜线:等同于判断行之差是否等于列之差也,即 a b s ( x [ k ] − x [ i ] ) ≠ a b s ( k − i ) x [ k ] ≠ x [ i ] \begin{array}{} abs(x[k]−x[i])\ne abs(k−i)\\ x[k]\ne x[i] \end{array} abs(x[k]−x[i])=abs(k−i)x[k]=x[i] - 搜索过程:
调用Check函数。
如果 边界条件,就继续调用放下一个皇后的位置 Check函数:
如果当搜索到第 N+1 行的时候,即代表前 N 行已经搜索完了,所以这个时候正好求出了一个解,记录加一。- 在当前位置上不满足条件的情形,进行回溯
搜索过程
![![[Pasted image 20240310171129.png]]](https://img-blog.csdnimg.cn/direct/5d957d90fa2c4eb1b1d48162b08f9f7b.png)
回溯,把放过的收起来
不是直接回溯到最开始,而是从第五行开始往第一行走,一层一层回溯,回到之前的每一行,继续往下一列走,判断有没有新的解,没有的话,就继续往前回溯
![![[Pasted image 20240310171558.png]]](https://img-blog.csdnimg.cn/direct/ef2174d22b0c4273b83c32324e73695c.png)
回溯到第二行,找到新的解,停止回溯,往后搜索,寻找新的解
![![[Pasted image 20240310171716.png]]](https://img-blog.csdnimg.cn/direct/c5e0544dfb3946faa883db5ddb2697fa.png)
找到新的解,ans+1,第五行没有别的解了,往前回溯
代码
C++ 语言描述:
占用的代码
#include <iostream>
#include <cstdio>
using namespace std;
int x[15] = {0}; //已知N小于10,建15没有问题
int sum,n;//判断是不是在同一列或者同一斜线上
int PD(int k)
{for(int i=1; i<k; i++){if(abs(k-i)==abs(x[k]-x[i]))return 0;else if (x[k]==x[i])return 0;//即判断是否符合条件来放,i表示皇后所在的行数,x[i]表示所在的列数,//所以前面那个条件用来判断两个皇后是否在对角线上,后面用来判断是否在同一列上。//行数不需要判断,因为他们本身的i就代表的是行数}return 1;
}bool check(int a)
{if(a>n) //当放到n+1的时候,代表前n个已经放好了sum++; //前面的放好了,ans+1elsereturn 0;return 1;
}void DFS(int a)
{if(check(a)) //判断是不是走到第n+1层,找到a了,直接返回return ;else //如果没找到,继续往下找for(int i=1; i<=n; i++) //从这一行的第一个往后放{if (x[a] != 0) //当前位置已被放过continue;x[a]=i; //第a个皇后放的列数,标记使用if(PD(a)) //判断是否能放这步DFS(a+1);//能的话进行下一个皇后的放置x[a] = 0;//释放现场//不能就下一列}
}
int main()
{cin>>n;//表示几个皇后DFS(1);//每次都从第一个皇后开始cout<<sum<<endl;return 0;
}
不占用的代码
#include <iostream>
#include <cstdio>
using namespace std;
int x[15] = {0};
int sum,n;int PD(int k)
{for(int i=1; i<k; i++){if(abs(k-i)==abs(x[k]-x[i]))return 0;else if (x[k]==x[i])return 0;//即判断是否符合条件来放,i表示皇后所在的行数,x[i]表示所在的列数,//所以前面那个条件用来判断两个皇后是否在对角线上,后面用来判断是否在同一列上。//行数不需要判断,因为他们本身的i就代表的是行数}return 1;
}bool check(int a)
{if(a>n)sum++;elsereturn 0;return 1;
}void DFS(int a)
{if(check(a))return ;elsefor(int i=1; i<=n; i++){x[a]=i;//第a个皇后放的列数if(PD(a))//判断是否能放这步DFS(a+1);//能的话进行下一个皇后的放置else continue ;//不能就下一列}
}
int main()
{cin>>n;//表示几个皇后DFS(1);//每次都从第一个皇后开始cout<<sum<<endl;return 0;
}
2. 图的路径搜索代表-路径之谜
题目链接
难度: 中等
标签: DFS, 2016, 国赛
题目描述:
小明冒充 X 星球的骑士,进入了一个奇怪的城堡。
城堡里边什么都没有,只有方形石头铺成的地面。
假设城堡地面是 n×n 个方格。如下图所示。
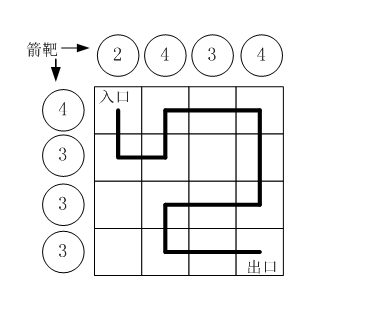
按习俗,骑士要从西北角走到东南角。可以横向或纵向移动,但不能斜着走,也不能跳跃。每走到一个新方格,就要向正北方和正西方各射一箭。(城堡的西墙和北墙内各有 n 个靶子)同一个方格只允许经过一次。但不必走完所有的方格。如果只给出靶子上箭的数目,你能推断出骑士的行走路线吗?有时是可以的,比如上图中的例子。
本题的要求就是已知箭靶数字,求骑士的行走路径(测试数据保证路径唯一)
输入:
第一行一个整数 N (0≤N≤20),表示地面有 N×N 个方格。
第二行 N 个整数,空格分开,表示北边的箭靶上的数字(自西向东)
第三行 N 个整数,空格分开,表示西边的箭靶上的数字(自北向南)
输出:
输出一行若干个整数,表示骑士路径。
为了方便表示,我们约定每个小格子用一个数字代表,从西北角开始编号: 0,1,2,3 ⋯⋯
输入输出样例:
输入
4
2 4 3 4
4 3 3 3
比如,上图中的方块编号为:
| 箭靶 | 2 | 4 | 3 | 4 |
|---|---|---|---|---|
| 4 | 0 | 1 | 2 | 3 |
| 3 | 4 | 5 | 6 | 7 |
| 3 | 8 | 9 | 10 | 11 |
| 3 | 12 | 13 | 14 | 15 |
输出
0 4 5 1 2 3 7 11 10 9 13 14 15
运行限制:
最大运行时间:1s
最大运行内存: 128M
解题思路:
这里用一个 N×N 的矩阵来表示城堡的位置,横向、纵向标号 1−N。
我们采用逆推法,既然原题目是走到哪里射一支箭,那我们就走到那里之后拔一支箭,如果最后得到所有的靶子上都没有箭了,由于题目的路径唯一,那就证明我们找到了题目所要求的路径。
- 算法开始:
当前行设为第一行,当前列设为第一列,从第一行第一列开始搜索。
然后从左上角初始位置,按照题目意思进行寻路。 - 判断边界:
在当前行,当前列的位置上判断是否满足条件,若不满足,跳到第 5 步,即不符合边界条件。 判断条件如下:- f l a g [ x ] [ y ] = = 1 flag[x][y]==1 flag[x][y]==1 标记数组已经被标记,已被走过,不能再走,超出边界
- x < 1 x<1 x<1 从左侧走出方格。
- x > n x>n x>n 从右侧走出方格。
- y < 1 y<1 y<1 从上侧走出方格。
- y > n y>n y>n 从下侧走出方格。
- c o l [ x ] < = 0 col[x]<=0 col[x]<=0 没走到右下角,箭用完了。
- r o l [ y ] < = 0 rol[y]<=0 rol[y]<=0 没走到右下角,箭用完了
- 搜索过程:
调用Check函数。 如果边界条件满足,就继续调用搜索,找到下一步的位置 - check(参数):
如果当搜索到 x = n , y = n x=n,y=n x=n,y=n 时,且靶子上的箭都没了,按就找到了答案。
按照题目输出即可。 - 在当前位置上不满足条件的情形,进行回溯,并还原现场
C++ 语言描述:
#include <bits/stdc++.h>using namespace std;struct PII
{int first;int second;
};const int N = 30;
int rol[N];
int col[N];
int n;//格子数 长宽从1到n
bool flag[N][N]; //用来标记是否走过
vector<PII> res;//---------图的路径搜索常用方向移动表示-------int dx[4]= {0,1,-1,0};
int dy[4]= {1,0,0,-1};// 两两组合形成上下左右四个方向
// 1------------------> x
// |
// |
// |
// |
// |
// |
// |
// ↓
// y// dx[0]=0 dy[0]=1 那么代表向下的方向
// dx[1]=1 dy[1]=0 那么代表向右的方向
// dx[2]=-1 dy[2]=0 那么代表向左的方向
// dx[3]=0 dy[3]=-1 那么代表向上的方向//--------------------------------------------bool check(int x, int y) //判断走过的路径的箭靶数是否与目标相同
{if(x==n && y==n) //表示走到右下角了{for(int i=1; i<=n; i++) //从1~n开始判断北边的靶子有没有箭{if(col[i]!=0){return false;}//如果箭靶上的数目不为0,根据逆推,我们通过当前路径得不到箭靶上的结果}for(int i=1; i<=n; i++) //判断西边的靶子上有没有箭{if(rol[i]!=0){return false;}//如果箭靶上的数目不为0,根据逆推,我们通过当前路径得不到箭靶上的结果}for(int i=0; i<res.size(); i++) //如果有,把答案进行输出{int x=res[i].first;//x 轴坐标int y=res[i].second;//y 轴坐标int sum=n*(x-1)+y-1 ;// 通过计算的到为题目要求的坐标系cout <<sum<< " ";}cout << endl;return false;// 成功终止}return true; //继续搜索//关于终止还是继续我们交给判定即可
}
bool pd(int x2,int y2) //边界判断
{if(flag[x2][y2]==1)return 0;//已被走过,不能再走,超出边界else if(x2<1)return 0;//从左侧走出方格else if(x2>n)return 0;//从右侧走出方格else if(y2<1)return 0;//从上侧走出方格else if(y2>n)return 0;//从下侧走出方格else if(col[x2]<=0)return 0;//没走到右下角,箭用完了else if(rol[y2]<=0)return 0;//没走到右下角,箭用完了else return 1;//符合边界条件,可以继续执行搜索
}void dfs(int x,int y)
{if(!check(x,y)) //判断是不是符合规则{return ;//包含不符合规则的地方,回溯,用于剪枝}else //如果符合规则,就扩展{for(int i=0; i<4; i++){int xt=dx[i]+x; //完成上下左右四个方向的移动int yt=dy[i]+y;if(!pd(xt,yt)){continue ;//不符合要求继续换方向搜索}else{//因为要进行位置转移,我们给它起个名字,叫作案现场//比如向下移动flag[xt][yt]=true; //搜索到这个点,把它标记起来col[xt]--; //北边拔一个箭rol[yt]--; //西边拔一个箭res.push_back({xt,yt}); //把每次路径的点放入vector//继续向下搜索dfs(xt,yt);//搜索回溯后,因为没有找到正确答案,所以要回复作案现场,返回到搜索之前res.pop_back();flag[xt][yt]=false;col[xt]++;rol[yt]++;}}}
}int main()
{cin >> n;for(int i=1; i<=n; i++)cin >> rol[i];for(int i=1; i<=n; i++)cin >> col[i];flag[1][1]=true;col[1]--;rol[1]--;res.push_back({1,1});dfs(1,1);return 0;
}