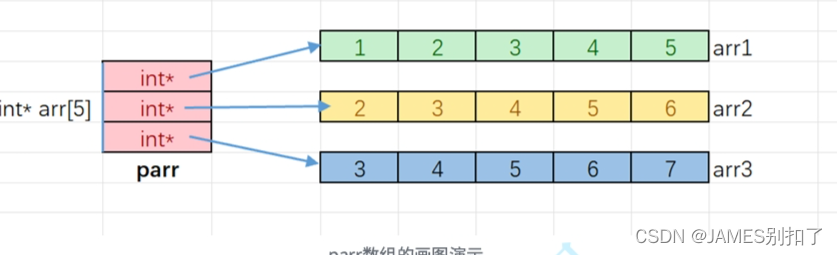
原文:普林斯顿大学算法课程
译者:飞龙
协议:CC BY-NC-SA 4.0
6.1 事件驱动模拟
原文:
algs4.cs.princeton.edu/61event译者:飞龙
协议:CC BY-NC-SA 4.0
本章节正在建设中。
根据弹性碰撞的法则使用事件驱动模拟模拟 N 个碰撞粒子的运动。这种模拟在分子动力学(MD)中被广泛应用,以理解和预测粒子级别的物理系统的性质。这包括气体中分子的运动,化学反应的动力学,原子扩散,球体堆积,围绕土星的环的稳定性,铈和铯的相变,一维自引力系统以及前沿传播。相同的技术也适用于其他涉及粒子系统的物理建模领域,包括计算机图形学,计算机游戏和机器人技术。我们将在第七章再次讨��其中一些问题。
一个好的参考资料
硬球模型. 硬球模型(台球模型)是容器中原子或分子运动的理想化模型。我们关注二维版本称为硬盘模型。这个模型的显著特性如下。
-
N 个运动中的粒子,限制在单位盒中。
-
粒子i具有已知位置(rx[i], ry[i])、速度(vx[i], vy[i])、质量m[i]和半径σ[i]。
-
粒子之间以及与反射边界之间通过弹性碰撞相互作用。
-
没有其他力的作用。因此,粒子在碰撞之间以恒定速度直线运动。
这个简单模型在统计力学中起着核心作用,这个领域将宏观可观测量(例如温度、压力、扩散常数)与微观动力学(单个原子和分子的运动)联系起来。麦克斯韦和玻尔兹曼使用这个模型推导出相互作用分子的速度分布与温度的关系;爱因斯坦用它来解释花粉颗粒在水中的布朗运动。
模拟. 有两种自然方法来模拟粒子系统。
-
时间驱动模拟. 将时间离散化为大小为dt的量子。在每个dt时间单位后更新每个粒子的位置并检查重叠。如果有重叠,将时钟回滚到碰撞时刻,更新碰撞粒子的速度,并继续模拟。这种方法简单,但存在两个重大缺点。首先,我们必须在每个时间量子中执行 N²次重叠检查。其次,如果dt太大,碰撞粒子在我们查看时未发生重叠,我们可能会错过碰撞。为了确保相对准确的模拟,我们必须选择dt非常小,这会减慢模拟速度。
-
事件驱动模拟. 通过事件驱动模拟,我们只关注发生有趣事件的时间点。在硬盘模型中,所有粒子在碰撞之间以恒定速度直线运动。因此,我们的主要挑战是确定粒子碰撞的有序序列。我们通过维护一个按时间排序的优先队列来解决这个挑战。在任何给定时间,优先队列包含所有未来可能发生的碰撞,假设每个粒子永远沿直线轨迹运动。随着粒子碰撞并改变方向,一些计划在优先队列上的事件变得“过时”或“无效”,不再对应物理碰撞。我们采取一种懒惰策略,将这些无效的碰撞留在优先队列上,等待识别并丢弃它们被删除时。主要的事件驱动模拟循环工作如下:
-
删除即将发生的事件,即具有最小优先级t的事件。
-
如果事件对应于无效的碰撞,将其丢弃。如果其中一个粒子自事件插入优先队列以来已经参与了碰撞,则该事件无效。
-
如果事件对应于粒子i和j之间的物理碰撞:
-
将所有粒子沿直线轨迹推进到时间t。
-
根据弹性碰撞的法则更新两个碰撞粒子i和j的速度。
-
确定所有未来可能涉及i或j的碰撞事件,假设所有粒子从时间t开始沿直线轨迹移动。将这些事件插入优先队列。
-
-
如果事件���应于粒子i和墙壁之间的物理碰撞,对粒子i执行类似的操作。
这种事件驱动的方法比时间驱动的方法产生了更健壮、更准确和更高效的模拟。
-
碰撞预测。 我们回顾了指定粒子是否以及何时与边界或其他粒子碰撞的公式,假设所有粒子都沿直线轨迹移动。
-
粒子与墙壁之间的碰撞. 给定时间t时粒子的位置(rx, ry)、速度(vx, vy)和半径σ,我们希望确定它是否以及何时会与垂直或水平墙壁碰撞。

由于坐标在 0 和 1 之间,如果ry + Δt vy等于σ或(1 - σ),则粒子在时间t + Δt 时与水平墙面接触。解出Δt得到:

一个类似的方程预测了与垂直墙壁的碰撞时间。
-
两个粒子之间的碰撞. 给定时间t时两个粒子i和j的位置和速度,我们希望确定它们是否以及何时相互碰撞。

让(rx[i]’ , ry[i]’ )和(rx[j]’ , ry[j]’ )表示粒子i和j在接触时刻,即t + Δt的位置。当粒子碰撞时,它们的中心相距σ = σ[i] + σ[j]的距离。换句话说:
σ² = (rx[i]’ - rx[j]’ )² + (ry[i]’ - ry[j]’ )²
在碰撞之前的时间内,粒子沿直线轨迹移动。因此,
rx[i]’ = rx[i] + Δt vx[i], ry [i]’ = ry[i] + Δt vy[i]
rx[j]’ = rx[j] + Δt vx[j], ry [j]’ = ry[j] + Δt vy[j]
将这四个方程代入前一个方程,解出得到的二次方程的Δt,选择物理相关的根,并简化,我们得到Δt的表达式,其中包括已知位置、速度和半径。


如果Δv ⋅ Δr ≥ 0 或 d < 0,则二次方程对Δt > 0 没有解;否则我们保证Δt ≥ 0。
碰撞解决方案。 在本节中,我们提供了指定粒子在与反射边界或其他粒子发生弹性碰撞后行为的物理公式。为简单起见,我们忽略多粒子碰撞。有三个方程控制着一对硬盘之间的弹性碰撞:(i) 线性动量守恒,(ii) 动能守恒,以及(iii) 碰撞时,法向力作用于碰撞点的表面垂直方向。对物理感兴趣的学生被鼓励从第一原理推导这些方程;其余的可以继续阅读。
-
粒子与墙壁之间。 如果具有速度(vx,vy)的粒子与垂直于x轴的墙壁碰撞,则新速度为(-vx,vy);如果与垂直于y轴的墙壁碰撞,则新速度为(vx,-vy)。
-
两个粒子之间。 当两个硬盘碰撞时,法向力沿着连接它们中心的线作用(假设没有摩擦或旋转)。在接触瞬间,完全弹性碰撞的法向冲量(Jx,Jy)在x和y方向上的作用是:

其中m[i]和m[j]分别是粒子i和j的质量,σ、Δx、Δy和Δ v ⋅ Δr如上所定义。一旦我们知道冲量,我们就可以应用牛顿第二定律(以动量形式)来计算碰撞后立即的速度。
vx[i]’ = vx[i] + Jx / m[i], vx[j]’ = vx[j] - Jx / m[j]
vy[i]’ = vy[i] + Jy / m[i], vy[j]’ = vy[j] - Jy / m[j]
Java 中的粒子碰撞模拟。 我们的实现涉及以下数据类型:MinPQ.java、Particle.java 和 CollisionSystem.java。
-
粒子数据类型。 代表在单位盒中移动的粒子。
-
事件数据类型。 表示碰撞事件的数据类型。有四种不同类型的事件:与垂直墙壁的碰撞、与水平墙壁的碰撞、两个粒子之间的碰撞和重绘事件。这将是一个很好的机会来尝试面向对象编程和多态性。我们提出以下更简单(但略显不够优雅)的方法。
为了实现
isValid,事件数据类型应该在事件创建时存储相关粒子的碰撞计数。如果粒子的当前碰撞计数与事件创建时的相同,则该事件对应于物理碰撞,即没有干预碰撞。
数据文件。 我们使用以下数据格式。第一行包含粒子数量 N。剩下的 N 行中,每行包含 6 个实数(位置、速度、质量和半径),后跟三个整数(颜色的红、绿、蓝值)。您可以假设所有位置坐标在 0 和 1 之间,颜色值在 0 和 255 之间。此外,您可以假设没有粒子相互交叉或与墙壁相交。
N
rx ry vx vy radius mass r g b
rx ry vx vy radius mass r g b
rx ry vx vy radius mass r g b
rx ry vx vy radius mass r g b这里是一些示例数据文件:
| 文件 | 描述 |
| p10.txt | 10 个粒子 |
|---|---|
| p2000.txt | 2000 个粒子 |
| diagonal.txt | |
| diagonal1.txt | |
| diagonal2.txt | |
| wallbouncing.txt | 一排有 9 个粒子与一列有 9 个粒子碰撞 |
| wallbouncing2.txt | 一排有 10 个粒子不与一列有 9 个粒子碰撞 |
| wallbouncing3.txt | 一排有 19 个粒子与一列有 19 个粒子碰撞 |
| p100-.125K.txt | 0.125 开尔温下的 100 个粒子 |
| p100-.5K.txt | 0.5 开尔温下的 100 个粒子 |
| p100-2K.txt | 2.0 开尔温下的 100 个粒子 |
| p1000-.5K.txt | 0.5 开尔温下的 1000 个粒子 |
| p1000-2K.txt | 2.0 开尔温下的 1000 个粒子 |
| billiards2.txt | 母球撞击 3 个球的金字塔 |
| billiards4.txt | 母球撞击 10 个球的金字塔 |
| billiards5.txt | 母球撞击 15 个球的金字塔 |
| diffusion.txt | 从裂缝一侧扩散的粒子 |
| diffusion2.txt | 从一个四分之一处扩散的粒子 |
| diffusion3.txt | |
| brownian.txt | |
| brownian2.txt | |
| squeeze.txt | 一个微小粒子夹在两个大粒子之间 |
| squeeze2.txt | 一个微小粒子夹在两个大颗粒之间 |
| pendulum.txt | 钟摆效应 |
其他潜在的数据文件
-
一个颗粒在运动。
-
两个颗粒正面碰撞。
-
两个颗粒,一个静止,以角度碰撞。
-
一个红色颗粒在运动,N 个蓝色颗粒静止。
-
N 个粒子在一个具有随机初始方向的晶格上(但速度相同),以使总动能与某个固定温度 T 一致,总线性动量= 0。 对于不同的 T 值,有不同的数据集。
-
扩散 I:在容器中心附近分配 N 个非常小的相同大小的粒子,具有随机速度。
-
扩散 II:左侧有 N 个蓝色颗粒,右侧有 N 个绿色颗粒,分配速度使它们热化(例如,离开它们之间的隔板并在一段时间后保存位置和速度)。 观察它们混合。 计算平均扩散速率?
-
N 个大颗粒,所以没有太多空间可以移动而不碰到东西。
-
爱因斯坦对布朗运动的解释:中间有一个大红色颗粒,N 个较小的蓝色颗粒。
练习
-
粒子碰撞游戏。 实现游戏Particles:你用鼠标控制一个红色球,试图避免与根据弹性碰撞定律行事的蓝色球碰撞。 一段时间后,随机引入一个新的蓝色球。
-
布朗运动。 1827 年,植物学家罗伯特·布朗使用显微镜观察了浸泡在水中的野花花粉颗粒的运动。 他观察到花粉颗粒是随机运动的,遵循后来被称为布朗运动的运动。 这种现象被讨论过,但直到爱因斯坦在 1905 年提供了一个数学解释之前,没有提供令人信服的解释。 爱因斯坦的解释:花粉颗粒的运动是由数百万微小分子与较大颗粒碰撞引起的。 他给出了描述在给定温度下悬浮在液体中的微小颗粒行为的详细公式。 爱因斯坦的解释旨在帮助证明原子和分子的存在,并可用于估计分子的大小。 爱因斯坦的布朗运动理论使工程师能够通过观察单个粒子的运动来计算合金的扩散常数。 这里有一个来自这里的 Einstein’s explanation of Brownian motion 演示。
-
自由程和自由时间。 自由程 = 粒子在碰撞之间行进的距离。 绘制直方图。 平均自由程 = 所有粒子的平均自由程长度。 随着温度的升高,平均自由程增加(保持压力恒定)。 计算自由时间长度 = 粒子与另一个粒子或墙壁碰撞之前经过的时间。
-
碰撞频率。 每秒碰撞次数。
-
均方根速度。 均方根速度 / 平均自由程 = 碰撞频率。均方根速度 = sqrt(3RT/M),其中摩尔气体常数 R = 8.314 J / mol K,T = 温度(例如,298.15 K),M = 分子质量(例如,氧气为 0.0319998 kg)。
-
麦克斯韦-玻尔兹曼分布。 在硬球模型中,粒子速度的分布服从麦克斯韦-玻尔兹曼分布(假设系统已经热化,粒子足够重,我们可以忽略量子效应)。 分布形状取决于温度。 每个分量的速度分布与 exp(-mv_x² / 2kT)成比例。 在 d 维中速度的大小分布与 v^(d-1) exp(-mv² / 2kT)成比例。 在统计力学中使用,因为模拟大约 10²³ 个粒子是不方便的。 原因:x,y 和 z 方向的速度是正态的(如果所有粒子质量和半径相同)。 在 2d 中,用 Rayleigh 代替麦克斯韦-玻尔兹曼。
-
压力。 感兴趣的主要热力学性质 = 平均压力。压力 = 分子碰撞对容器施加的单位面积的力。在二维中,压力 = 容器壁上单位长度的平均力。
-
温度。 绘制随时间变化的温度(应保持恒定)= 1/N sum(mv²) / (d k),其中 d = 维度 = 2,k = 玻尔兹曼常数。
-
扩散。 分子移动非常迅速(比喷气机更快),但扩散缓慢,因为它们与其他分子碰撞,从而改变它们的方向。两个通过管道连接的容器,其中包含两种不同类型的粒子。随时间变化测量每种类型粒子在每个容器中的比例。
-
时间可逆性。 改变所有速度并向后运行系统。忽略舍入误差,系统将返回到其原始状态!
-
麦克斯韦的恶魔。 麦克斯韦的恶魔是詹姆斯·克拉克·麦克斯韦于 1871 年构想出来的一个思想实验,旨在反驳热力学第二定律。中间有垂直墙壁,带有分子大小的陷阱门,左半部分有 N 个粒子,右半部分也有 N 个粒子,只有恶魔允许通过的粒子才能通过陷阱门。恶魔让左到右速度比平均速度快的粒子通过,让右到左速度比平均速度慢的粒子通过。可以利用能量重新分配来运行热机,允许热量从左到右流动。(不违反法则,因为恶魔必须与物理世界互动以观察分子。恶魔必须存储关于分子在陷阱门哪一侧的信息。恶魔最终会耗尽存储空间,必须开始擦除先前积累的信息以为新信息腾出空间。这种信息的擦除增加了熵,需要 kT ln 2 单位的工作。)
-
度量空间。 扩展以支持任意度量空间中的球体和超平面。
-
细胞方法。 有用的优化:将区域划分为矩形单元。确保粒子只能在任何时间量子中与九个相邻单元中的粒子发生碰撞。减少必须计算的二元碰撞事件数量。缺点:必须监视粒子在单元之间移动的过程。
-
多粒子碰撞。 处理多粒子碰撞。在模拟台球游戏中的碰撞时,这种碰撞非常重要。
-
动态堆或动态数据结构。(Guibas)
创意练习
6.2 B 树
原文:
algs4.cs.princeton.edu/62btree译者:飞龙
协议:CC BY-NC-SA 4.0
本章正在进行重大改建。
问答
练习
6.3 后缀数组
原文:
algs4.cs.princeton.edu/63suffix译者:飞龙
协议:CC BY-NC-SA 4.0
本章正在大规模施工中。
重要说明。
*从 Oracle 和 OpenJDK Java 7,Update 6 开始,substring()方法在提取的子串大小上花费线性时间和空间(而不是常数时间和空间)。String API对其所有方法,包括substring()和charAt(),都不提供性能保证。
课本和书站中的程序已经更新,不再依赖于常数时间的子串操作。但是,如果您使用的是课本的第三版印刷版(或更早版本),请自行考虑。*
后缀排序和后缀数组。
后缀排序:给定一个字符串,按升序对该字符串的后缀进行排序。排序后的列表称为后缀数组。程序 SuffixArray.java 构建了一个后缀数组数据结构。
最长重复子串。
将排序应用于计算生物学和抄袭检测。程序 LongestRepeatedSubstring.java 使用后缀数组解决了这个问题。
上下文关键词(KWIC)。
给定后缀数组,通过二分搜索很容易搜索字符串或句子。内存是线性的。搜索是 O(K log N),其中 K 是您要搜索的字符串的长度。(通过使用 lcp 数组,可以在 K + log N 内完成。)有时被称为 KWIK(关键词上下文)和共现。被语言学家使用。Concordancer = 制作索引的程序。马丁·阿贝格(Martin Abegg)曾经将死海古卷的索引反向工程并转换为可读文本。程序 KWIK.java。
Manber 算法。
然而,输入大小为 N,因此我们可能希望利用子串的重叠性质并取得更好的效果。程序 Manber.java 使用 Manber-Myers 重复加倍算法的版本对字符串后缀进行排序。Larsson在内部排序例程替换为 O(N log N)基于比较的排序算法时给出了 O(N log N)的分析。
Kasai 算法。
这里是描述Kasai 算法计算 lcp 数组的内容。
问答
线性时间后缀排序。
倾斜分治。最简单的线性时间后缀排序解决方案。递归地对索引为{0, 1, 2} mod 3 的后缀进行排序,然后合并。
练习
-
给出字符串"abacadaba"的后缀数组。此外,给出 i 从 1 到 n-1 的
lcp(i)值表。 -
对字符串"mississippi"重复上一个问题。
-
创建一个长度为 n 的
SuffixArray对象需要多少字节? -
下面的代码片段计算后缀排序的所有后缀有什么问题?
suffix = ""; for (int i = s.length() - 1; i >= 0; i--) {suffix = s.charAt(i) + suffix;suffixes[i] = suffix; }答案:二次时间 和 二次空间。
-
下面的代码片段计算后缀排序的所有循环后缀有什么问题?
int n = s.length(); for (int i = 0; i < n; i++)suffixes[i] = s.substring(i, n) + s.substring(0, i);答案:二次时间 和 二次空间。
-
下面的代码片段计算后缀排序的所有循环后缀有什么问题?
int n = s.length; StringBuilder ss = new StringBuilder(); ss.append(s).append(s); for (int i = 0; i < N; i++)suffixes[i] = ss.substring(i, i + n);答案:二次时间 和 二次空间。
-
最长公共子串。 编写一个程序 LongestCommonSubstring.java,接受两个文件名作为命令行参数,读取这两个文本文件,并找到两者中都出现的最长子串。提示:为 s#t 创建一个后缀数组,其中 s 和 t 是两个文本字符串,#是两者都不出现的字符。
1970 年,D. Knuth 猜想在线性时间内解决这个问题是不可能的。事实上,可以使用后缀树或后缀数组在线性时间内(在最坏情况下)解决这个问题。
-
Burrows-Wheeler 变换。 Burrows-Wheeler 变换(BWT)是数据压缩算法中使用的一种转换,包括 bzip2 和基因组学中的高通量测序。给定长度为 N 的文本字符串(以特殊的文件结束符 $ 结尾,比任何其他字符都小),考虑 N×N 矩阵,其中每行包含原始文本字符串的不同循环旋转。按字典顺序对行进行排序。Burrows-Wheeler 变换是排序矩阵中的最右列。例如,BWT (mississippi ) = i p s s m ) = ipssm )=ipssmpissii。
-
Burrows-Wheeler 逆变换。 Burrows-Wheeler 逆变换(BWI)用于反转 BWT。给定文本字符串的 BWT,设计一个线性时间算法来恢复原始文本字符串。例如,BWI(ipssm p i s s i i ) = m i s s i s s i p p i pissii) = mississippi pissii)=mississippi。
-
循环字符串线性化。 给定一个字符串 s,找到字典序最小的旋转。在化学数据库中用于循环分子。每个分子表示为循环字符串。规范表示是字典序最小的旋转。设计一个算法来计算循环字符串的规范表示 提示:后缀排序。
其他解决方案:Duval 算法使用 Lyndon 分解和由周元提出的令人惊讶优雅的最小表达算法。
-
加速排名。 使用以下思想加速
rank()方法中的二分搜索。让lo和hi表示当前搜索区间的左右端点。让lcpLo表示查询字符串和suffixes[lo]的 lcp,让lcpHi表示查询字符串和suffixes[hi]的 lcp。然后,在将查询字符串与suffixes[mid]进行比较时,只需要比较从lcp = min(lcpLo, lcpHi)开始的字符,因为搜索区间中的所有后缀都具有相同的前lcp个字符。 -
加速排名分析。 显示加速排名的最坏情况运行时间仍然与 L log N 成正比,其中 L 是查询的长度,N 是文本的长度。然而,Myers 和 Manber 报告说这在实践中加快了计算。理论上,可以使用非相邻的 lcp 值将其改进为 L + log N。
-
最长 3 重复子串。 给定一个文本字符串,找到重复 3 次或更多次的最长子串。
-
最长 k 重复子串。 给定一个文本字符串和一个整数 k,找到重复 k 次或更多次的最长子串。
-
长重复子串。 给定一个文本字符串和一个整数 L,找到所有长度大于等于 L 的重复子串。
-
三个字符串中的最长公共子串。 给定三个字符串 r、s 和 t,找到在所有三个字符���中出现的最长子串。
-
最长公共反向互补子串。 给定两个 DNA 字符串,找到出现在一个字符串中的最长子串,其反向 Watson-Crick 互补出现在另一个字符串中。如果 t 是 s 的反向,除了以下替换 AT、CG,则两个字符串 s 和 t 是反向互补的。例如 ATTTCGG 和 CCGAAAT 是彼此的反向互补。 提示:后缀排序。
-
具有更少内存的后缀数组。 不使用子字符串数组,其中
suffixes[i]指的是第 i 个排序后缀,而是维护一个整数数组,其中 index[i] 指的是第 i 个排序后缀的偏移量。要比较由 a = index[i] 和 b = index[j] 表示的子字符串,比较字符s.charAt(a)与s.charAt(b),s.charAt(a+1)与s.charAt(b+1),依此类推。你节省了多少内存?你的程序更快吗? -
k-gram 频率计数。 给定一个文本字符串,设计一个数据结构以高效地回答以下形式的查询:给定一个 k-gram 出现了多少次?在最坏情况下,时间复杂度应该与 k log N 成正比,其中 k 是 k-gram 的长度,N 是文本字符串的长度。
-
最频繁的 k-gram。 给定一个文本字符串和一个整数 k,找到出现频率最高的 k-gram。
-
最短唯一子串。 给定一个文本字符串,找到一个出现仅一次的最短子串。这个问题常见于生物信息学。
-
最短非子串。 给定一个比特串,找到一个最短的比特串,它不作为子串出现。
-
最短唯一子串。 给定一个文本字符串,预处理它以回答以下形式的最短唯一子串查询:给定一个索引 q 到文本字符串,找到一个包含索引 q 且在文本中其他地方不作为子串出现的最短子串。
6.4 最大流
原文:
algs4.cs.princeton.edu/64maxflow译者:飞龙
协议:CC BY-NC-SA 4.0
本节正在大规模建设中。
最大流和最小 s-t 割。
程序 FordFulkerson.java 在 E² V 时间内使用 Edmonds-Karp 最短增广路径启发式方法计算带权有向图中的最大流和最小 s-t 割(尽管在实践中,它通常运行得更快)。它使用 FlowNetwork.java 和 FlowEdge.java。
渗透。
2D(始终选择最左边的路径)和 3D 中的最大流。
应用于计算机图形学。
Yuri Boykov在计算机视觉中的分割应用中有关于最大流的论文。maxflow data。
二部图匹配。
练习
-
**包含两个顶点的循环。**给定一个无向图 G 和两个特殊顶点 s 和 t,找到包含 s 和 t 的循环(不一定是简单的),或报告不存在这样的循环。您的算法应该在线性时间内运行。
答案。当且仅当从 s 到 t 的最大流至少为 2 时,答案是肯定的。因此,在每条边都替换为两条反向边和单位容量的有向图中运行 Ford-Fulkerson 的两次迭代。
-
**k-连通。**给定一个无向图,确定两个顶点 s 和 t 是否 k-连通(或等价地,是否存在 k 条边不相交的路径)。
-
真或假。如果为真,请提供简短的证明,如果为假,请给出一个反例。
-
在任何最大流中,没有一个有正流量的有向循环。
-
存在一种最大流,其中没有一个有正流量的有向循环。
-
如果所有边的容量都不同,最大流是唯一的。
-
如果所有边的容量都不同,最小割是唯一的。
-
如果所有边的容量增加一个加法常数,最小割保持不变。
-
如果所有边的容量乘以一个正整数,最小割保持不变。
-
-
**包含两个顶点的简单循环。**给定一个无向图和两个顶点 s 和 t,找到包含 s 和 t 的简单循环(或报告不存在这样的循环)。
提示:当且仅当存在两个(内部)顶点不相交的路径时,包含 s 和 t 的有向循环才存在。
-
**有向图中的顶点不相交路径。**给定一个有向图 G 和两个顶点 s 和 t,找到从 s 到 t 的最大数量的顶点不相交路径。
提示:将每个顶点 v(除了 s 和 t 之外)替换为两个顶点 v1 和 v2;从 v1 到 v2 添加容量为 1 的边;将所有指向 v 的边重定向到 v1;将所有从 v 指向的边重定向到 v2。
-
**无向图中的顶点不相交路径。**给定一个无向图 G 和两个顶点 s 和 t,找到 s 和 t 之间的最大数量的顶点不相交路径。
提示:将每条无向边 v-w 替换为两条有向边 v->w 和 w->v。
-
**包含三个顶点的简单路径。**给定一个无向图和三个顶点 u、v 和 w,找到包含 u、v 和 w 的简单路径(或报告不存在这样的路径)。
提示:当且仅当存在两个(内部)顶点不相交的路径,一个从 v 到 u,一个从 v 到 w 时,u 和 w 之间存在一个通过 v 的简单路径。
-
**唯一最小割。**给定一个 s-t 流网络,确定最小割是否唯一。
提示:在 G 和 G^R 中解决 s-t 最小割问题。
-
**二部图中的不可匹配边。**给定一个二部图 G,如果边不出现在 G 的任何完美匹配中,则该边是不��匹配的。
提示:如果 G 没有完美匹配,那么所有边都是不可匹配的。否则,找到一个完美匹配;将完美匹配中的所有边定向为一个方向,将所有剩余的边定向为相反的方向;不在完美匹配中且端点在结果有向图的不同强连通分量中的边都是不可匹配的边。
-
具有最少边的最小割。 给定一个流网络,在所有最小割中,找到一个具有最少边数的割。
提示:创建一个新的流网络 G’,它等于 G,除了 w’(e) = w(e) * n + 1。
6.5 归约
原文:
algs4.cs.princeton.edu/65reductions译者:飞龙
协议:CC BY-NC-SA 4.0
本章节正在建设中。
归约。
在计算机科学中,归约或模拟是一个强大的概念… 将问题 X 转化为一个更简单的问题 Y 的问题解决框架,以便根据 Y 的解推导出原始问题 X 的解。
Eric Alander - “归约提供了一种抽象。如果 A 高效地归约到 B,且 B 高效地归约到 A,那么 A 和 B 在某种意义上是等价的:它们是观察同一问题的两种不同方式。我们不再有无限多的计算问题,而是留下了更少数量的等价问题类。没有什么能让计算社区为这一惊人的洞察做好准备,即人们真正想要解决的计算问题只有几个。根据资源限制将自然计算问题划分为有意义的组别。”
上界。
-
3-共线到排序。
-
凸包到排序(Graham 扫描)。
-
中位数到排序。
-
二分图匹配到最大流。BipartiteMatchingToMaxflow.java 通过将问题归约为最大流,在二分图中计算最大基数匹配。在最坏情况下,每次增广都会增加匹配的基数。Hopcroft-Karp 算法将运行时间改进为 E sqrt(V)。
-
LP 标准形式:标准形式线性规划是 { max cx : Ax <= b, x ≥ 0 }。展示如何将一般线性规划(带有 ≤、≥ 和 = 约束)归约为标准形式。
-
最大流到线性规划。
-
分配问题到线性规划。
-
PERT 到 有向无环图的拓扑排序。
-
USTCONN(无向图中的 s-t 连通性)到 STCONN(有向图中的无向 s-t 连通性)。
-
无向图上的最短路径到有向图上的最短路径。
-
欧几里得最小生成树到 Delauney 三角剖分。
-
LP 可行性归约为 LP。(使用二分搜索。需要限制有界 LP 的值。)
-
二人零和博弈到 LP。TwoPersonZeroSumGame.java
-
LP 可归约为二人零和博弈。(Bradley, Hax, 和 Magnanti 的练习 26)
下界。
-
元素唯一性到排序。
-
2D 最近点对问题到 2D 欧几里得最小生成树。
-
凸包到 Voronoi / Delauney 三角剖分。
-
3-SUM 到 3-共线。
-
练习:3-SUM 到 4-SUM。
-
练习:3-SUM 到 3-SUMplus
-
练习:3-共线到 3-共点。
-
3-SAT 到 独立集。
-
独立集到整数线性规划。
-
元素唯一性。 给定 N 个来自全序宇宙的元素 x[1], …, x[n],是否存在一对 i ≠ j,使得 x[i] = x[j]?在比较树模型和代数决策树模型中有 Theta(N log N) 的下界。通过排序可以轻松达到 O(N log N)。
解决方案 1(比较树模型):给定 N 个不同的值。让 ai 成为第 i 小的元素。在任何基于比较的算法中,我们必须比较 a[i] 和 a[i-1];否则算法无法区分 a[i-1] < a[i] 和 a[i-1] = a[i] 的情况。考虑 N 个元素的两种不同排列。存在一个元素 a[i],在第一个排列中 a[i-1] 在 a[i] 之前,但在第二个排列中 a[i-1] 在 a[i] 之后。由于每个基于比较的算法必须比较 a[i] 和 a[i-1],算法在这两个排列上运行不同。因此,至少有 N! 个叶子节点。参考链接
解法 2(比较树模型):假设元素都是不同的且 a_1 < a_2 < … < a_N。任何正确的元素唯一性算法必须对每个 i < N 比较 a_i 和 a_i+1。如果不这样做,那么如果我们将 a_i+1 更改为 a_i,算法将产生相同的输出(但这将从无重复更改为有重复的答案)。算法使用的比较集合形成一个 DAG。找到总顺序(线性时间)并得到排序顺序。因此,该算法可用于对不同元素进行排序,且排序下界适用。
备注:这些论点适用于比较树模型的计算,但不适用于线性决策树或代数决策树模型的计算。这里有一个更一般的论点(由 Jeff Erickson 提供):考虑所有可能输入的空间 R^n。正输入的集合有 n!个连通分量,每个排列一个。另一方面,可以到达线性决策树中任何叶子的输入子集是凸的,因此是连通的。因此,任何确定唯一性的线性决策树至少有 n!个叶子。线性决策树的结果是由 Dobkin 和 Lipton 在On the complexity of computations under varying sets of primitives.中得出的。代数决策树的结果是由 Ben-Or 在Lower bounds for algebraic computation trees.中得出的。整数输入的特殊情况的结果更微妙:参见 Lubiw 和 Racs 的整数元素唯一性问题的下界。
-
3-SUM。
-
3-SAT。
线性规划。
将线性方程组推广到不等式。
讲座幻灯片
单纯形算法。
由 George Dantzig 于 1948 年发明。根据 Dongarra 和 Sullivan 的说法,单纯形算法是 20 世纪对科学和工程影响最大的十大算法之一。广义的高斯消元以处理不等式。程序 LinearProgramming.java 是一个基本实现。它解决{ max cx : Ax <= b, x >= 0 }假设 b >= 0。因此 x = 0 是一个基本可行解(我们不需要担心单纯形的第一阶段)。
线性规划的基本定理。形式为(P)的每个 LP 都具有以下三个属性:(i)如果它没有最优解,则它要么是不可行的,要么是无界的(ii)如果它有一个可行解,则它有一个基本可行解(iii)如果它有一个最优解,则它有一个基本最优解。
强对偶定理。形式为(P)的每个 LP 都有一个对偶(D){ min by : y A >= c : y >= 0 }。p1 + p2 + … + pM = 1 -> x1 + x2 + … + xm = 1/V。
如果(P)有���且可行,则(D)也有界且可行。此外,它们具有相同的最优值。单纯形算法同时解决这两个问题。
显著特性。实践中,单纯形算法通常在最多 2(m+n)个主元中终止。n = 总变量(原始+松弛),m = 方程。
陷阱。退化,循环。
分配问题。
形式化为 LP。依赖于 Birchoff-von Neumann 定理:分配问题 LP 的所有极端点都是 {0, 1}。AssignmentProblemToLP.java 将分配问题(最大权重完美匹配)简化为线性规划。EasyAssignmentProblemToLP.java 将所有内容放在主函数中,不提取对偶解。Hungarian.java 实现了匈牙利算法;在最坏情况下,运行时间的增长数量级为 N⁴。 --> AssignmentProblem.java 实现了连续最短路径算法;在最坏情况下,运行时间的增长数量级为 N³ log N。AssignmentProblemDense.java 实现了连续最短路径算法;在最坏情况下,运行时间的增长数量级为 N³。
二人零和博弈。
简化为 LP。可以假设收益矩阵严格为正(对每个条目添加一个常数会使游戏的价值增加 M,但不会改变解)。(P)min { x1 + … + xm, : x >= 0, M^t x >= 1} 和(D)max { y1 + … + yn, : y >= 0, My <= 1}。将解向量 x* 和 y* 标准化,以获得行玩家(最小化)和列玩家(最大化)的最佳策略;标准化常数是游戏的价值。
技巧。替换变量:xi = pi / V;最大化 V -> 最小化 1/V;博弈论,第 6-7 页
程序 ZeroSumGame.java 实现了这种方法。
注意:通过适当的变量更改,任何 LP 都可以转化为这种形式。
极小极大定理。(冯·诺伊曼)。对于每个有限的二人零和博弈,存在一个值 V 和每个玩家的混合策略,使得(i)给定行玩家的策略,列玩家的最佳可能收益是 V,以及(ii)给定列玩家的策略,行玩家的最佳可能收益是 -V。
线性规划求解器。
-
LinearProgramming.java 是单纯形算法的简化版本。假设 b >= 0,因此 x = 0 是一个起始的基本可行解。TwoPhaseSimplex.java 是两阶段单纯形算法的简化版本,它消除了假设 b >= 0。
-
OR-Objects 包含一个 Java 线性规划求解器。LPDemo.java 演示了如何使用 or124.jar 解决线性规划问题。
-
QSopt 是由大卫·阿普尔盖特、威廉·库克、Sanjeeb Dash 和 Monika Mevenkamp 创造的 Java 线性规划求解器。可以免费用于研究或教育目的。QSoptSolver.java 解决了 LP 格式的线性规划问题,例如 beer.lp。
-
Matlab 包含优化工具箱中的线性规划求解器。
[wayne:tombstone] ~> matlab< M A T L A B (R) >Copyright 1984-2009 The MathWorks, Inc.Version 7.9.0.529 (R2009b) 64-bit (glnxa64)August 12, 2009 >> A = [5 15; 4 4; 35 20]; >> b = [480; 160; 1190]; >> c = [13; 23];>> lb = [0; 0]; >> ub = [inf; inf]; >> x = linprog(-c, A, b, [], [], lb, ub) x =12.000028.0000 -
CPLEX 是用于线性规划、混合整数规划和二次规划的高性能数学规划求解器。支持与 C、C++、Java、Python、Matlab 和 Microsoft Excel 的接口。也可通过建模系统(包括 AIMMS、AMPL、GAMS 和 MPL)访问。
-
AMPL 是数学规划的建模语言。文件 beer.mod 和 beer.dat 指定了酿酒厂问题的模型和数据。
[wayne:tombstone] ~> ampl ILOG AMPL 9.100 AMPL Version 20021038 (SunOS 5.8)ampl: model beer.mod;ampl: data beer.dat;ampl: solve; ILOG CPLEX 9.100 CPLEX 9.1.0: optimal solution; objective 800 2 dual simplex iterations (1 in phase I)ampl: display x; x [*] := ale 12 beer 28 ;ampl: display constraints.dual; x [*] := corn 1 hops 2 malt 0 ; -
Microsoft Excel 在 Windows 上有一个基本的求解器插件,但在 Mac 上不再可用。
问答
Q. 无向最短路径与带负权重的有向最短路径?
A. 需要更聪明的简化来避免负循环(通过非二部匹配)。
练习
-
最大公约数和最小公倍数. 将最小公倍数简化为最大公约数。
-
表 k-和. 给定一个 k 行 N 列的整数表,是否有 k 个数相加为 0,每个数来自 k 行中的一个?
-
硬币不同。 给定 N 枚硬币和一个天平,确定这些硬币是否都有不同的重量。证明解决该问题的任何算法的复杂度至少为 N log N。提示:你可以使用这样一个事实,即给定 N 个实数,元素的不同性在线性决策树模型中至少需要 N log N 次比较(在这个模型中,你可以对 N 个元素的任意线性组合进行比较,例如,x1 + 2x2 < x3)。
-
集合相等。 给定两个集合 S 和 T,S 是否等于 T?给出一个 O(N log N)的算法和一个匹配的下界。
-
集合子集。 给定两个集合 S 和 T,S 是否是 T 的子集?给出一个 O(N log N)的算法和一个匹配的下界。
-
集合不相交。 给定两个集合 S 和 T,S 与 T 的交集是否为空集?给出一个 O(N log N)的算法和一个匹配的下界。(由于 S 和 T 是集合,因此两者中没有重复元素。)
解决方案。 要获得 O(N log N)的上界,对 S 和 T 中的元素的并集进行排序,并检查重复项。
-
集合不相交。 给定两个按升序排列的集合 S 和 T,S 与 T 的交集是否为空集?证明一个 Omega(N log N)的下界或给出一个 O(N)的算法。
-
合并两个列表的下界。 展示任何基于比较的合并两个大小为 N 的列表的算法在最坏情况下至少需要 2N-1 次比较。解决方案:即使所有元素都不同,下界也成立。如果第 i 个和第(i+1)个最小的元素在不同的列表中,则它们必须进行比较。
-
二分查找的下界。 需要 log(N+1)次比较。解决方案:即使所有元素都不同,下界也成立……
-
欧几里得 TSP 和 MST 下界。 对于欧几里得 TSP 或欧几里得 MST,给出一个 Omega(N log N)的下界(需要代数决策树来理解,因为你希望允许一个合理的算法来计算距离)。解决方案:在一条线上选择 N 个点。最优路径必须按升序访问这些点。
-
模式的下界。 模式的 Theta(N log N)下界。解决方案:可以通过找到模式并检查是否超过一个来解决元素不同性问题。
-
最接近对的下界。 最接近对的 Theta(N log N)下界。解决方案:如果有一个次线性对数算法,可以通过找到最接近对并检查它们是否相等来在次线性对数时间内解决元素不同性问题。
-
最小和次小元素。 描述如何使用最多 N + log N 次比较找到最小和次小元素。解决方案:将元素分成一对一对,并比较每对中的两个元素。使用每对中的 N/2 个获胜者进行递归。经过 N-1 次比较后,我们得到最小元素。请注意,每个元素最多与 log N 个其他元素进行比较。特别是,最小元素最多与 log N 个其他元素进行比较,其中一个必须是次小元素。如果你跟踪所有的比较,你可以记住涉及最小元素的 log N 次比较,并进行比较。
-
计数逆序对。 证明 Theta(N log N)的下界。这是一个尚未解决的研究问题。
-
螺母和螺栓。 证明快速排序部分的螺母和螺栓问题的 Theta(N log N)下界。[已知匹配的最坏情况上界为 O(N log N),但这是非常复杂的。]
-
存在符号表。 假设你有一个支持插入和存在操作的基于比较的算法,每次操作都只需要 O(1)次比较。解释为什么在这种计算模型中这是不可能的。解决方案:为了在 O(N)时间内解决元素不同性问题,对于每个 N 个元素,检查它是否已经在数据结构中(如果是,则这是一个重复项);如果不是,则插入它。
-
使用整数规划模型一个形如 x ≤ y 的约束(Ax = b,x >= 0,x 为整数)。
-
使用整数规划模型一个形如 x = {0 或 1}的约束。
-
使用整数规划模型一个形如 x = {1 或 2 或 4}的约束。
-
Tait 着色。 使用 IP 模拟 3 边着色立方图。
-
为患者分配器官捐赠者。
-
二部顶点覆盖。 减少到最大流。
-
传递闭包和传递闭包。 将传递闭包减少到传递闭包,反之亦然(当运行时间仅作为顶点数 V 的函数时)。也可减少到布尔矩阵乘法。
-
3SUM’。 给定三组整数 A、B 和 C,总大小为 n,是否存在 A 中的 a,B 中的 b 和 C 中的 c,使得 a + b = c?证明 3SUM 线性时间减少到 3SUM’,反之亦然。
解决方案。 要显示 3SUM 减少到 3SUM’,设置 A = S,B = S,C = -S。
要显示 3SUM’减少到 3SUM,假设所有整数都是正数(如果不是,则将 k 添加到 A 和 B 中的每个元素,将 2K 添加到 C 中的每个元素)。设置 m = 2 max(A, B, C)。对于 A 中的每个元素 a,在 S 中放置 a + m。对于 B 中的每个元素 b,在 S 中放置 b。对于 C 中的每个元素,在 S 中放置-c -m。
-
不等式满足等式。 给定线性不等式系统A x ≤ b,设计一个线性规划来确定在任何可行解x中哪些不等式必须满足等式。
-
等式约束。 使用两个<=约束模拟线性规划等式约束。
-
无限制变量。 使用两个非负变量 y 和 z 来模拟线性规划无限制变量 x。
-
无界 LP。 如果(P)是无界的,则存在一个矢量 d >= 0,使得 Ad <= 0 且 cd > 0。首先解释为什么如果存在这样的矢量 d,则问题是无界的。接下来,修改单纯形算法,在 LP 无界时报告这样的矢量。答案:根据假设 b >= 0 且 x = 0 是可行的。因此,对于任何正常数α,αd 都是可行的,并且具有目标值αcd。通过检查最小比率规则是否失败,可以识别矢量 d。在这种情况下,列 q 中的条目为非正(Ad <= 0),并且目标函数系数为正(cd > 0)。
-
减少成本。 修改单纯形算法以报告减少的成本(影子价格)。给出经济解释。
-
丹齐格的最陡边规则。 修改单纯形算法,使其始终选择最正的目标函数系数。
-
循环。 给出一个导致单纯形算法(使用最陡边规则)循环的病态线性规划输入。
-
瓶颈分配问题。 给定 N 个男人和 N 个女人。每个人有 M 个属性。每个人指定异性的一组理想属性。找到一个完美匹配,其中最不幸的人与指定属性最少的伴侣匹配。将此问题减少到分配问题。
解决方案。 创建一个边权重图,其中边的权重是两个人中满足的可取属性的最小数量。目标是最大化分配中最小权重边的权重。解决此问题的一种方法是使用二分查找(消除所有权重小于给定阈值的边)并解决结果的二部完美匹配问题。
-
中国邮递员问题。 给定一个强连通的有向图 G,找到一个最短长度的有向循环,该循环至少经过每条边一次。(事实证明,最佳循环将最多访问每条边两次。)如果每个顶点都是平衡的,则图是欧拉图:其度等于其出度。将不平衡的顶点分为两组:L = 出度小于入度的顶点,R = 出度大于入度的顶点。通过在 L 中的一个顶点到 R 中的一个顶点添加一个有向路径,我们改善了平衡性。在 (L, R) 上形成一个加权二部图,其中从 v 到 w 的边的权重是 G 中从 v 到 w 的最短路径的长度。找到一个最小权重匹配,并将这些边添加到 G 中使其成为欧拉图。然后,找到一个循环。这被称为 Edmonds-Johnson(1973)算法。(类似的算法适用于无向图,但需要在非二部图中找到一个最小权重完美匹配。)
6.6 难解性
原文:
algs4.cs.princeton.edu/66intractability译者:飞龙
协议:CC BY-NC-SA 4.0
本节正在建设中。复杂性理论的目标是理解高效计算的本质。我们已经学习了算法分析,这使我们能够根据它们消耗的资源量对算法进行分类。在本节中,我们将学习一个丰富的问题类别,至今还没有人能够设计出高效的算法。
计算复杂性。
随着数字计算机在 1940 年代和 1950 年代的发展,图灵机成为计算的理论模型。在 1960 年代,Hartmanis 和 Stearns 提出了将计算机所需的时间和内存作为输入大小的函数来衡量。他们以图灵机为基础定义了复杂性类,并证明了一些问题具有“无法通过巧妙编程规避的固有复杂性”。他们还证明了直观观念的一个正式版本(时间层次定理),即如果给予更多时间或空间,图灵机可以计算更多事物。换句话说,无论问题有多难(时间和空间要求),总会有更难的问题。
计算复杂性是确定不同问题的资源需求的艺术和科学。计算复杂性涉及对任何可能的问题算法的断言。做出这样的断言比理解问题的一个特定算法的运行时间要困难得多,因为我们必须推理所有可能的算法(甚至是尚未发现的算法)。这使得计算复杂性成为一个令人兴奋但又令人望而生畏的研究领域。我们将概述一些其最重要的思想和实际产物。
多项式时间。
我们已经分析了算法的运行时间作为其输入大小的函数。在解决给定问题时,我们更喜欢一个需要 8 N log N 步的算法,而不是需要 3 N² 步的算法,因为当 N 很大时,第一个算法比第二个算法快得多。第二个算法最终会解决相同的问题(但可能需要几小时而不是几秒)。相比之下,指数时间算法具有不同的定性行为。例如,对于 TSP 的暴力算法可能需要 N! 步。即使宇宙中的每个电子(10⁷⁹)都具有今天最快超级计算机(每秒 10¹² 条指令)的能力,并且每个电子在解决问题上工作了宇宙寿命(10¹⁷ 秒),也几乎无法解决 N = 1,000 的问题,因为 1000! >> 10¹⁰⁰⁰ >> 10⁷⁹ * 10¹² * 10¹⁷。指数增长使技术变革相形见绌。我们将任何运行时间受输入大小多项式限制的算法(例如 N log N 或 N²)称为多项式时间算法。如果问题没有多项式时间算法,则称该问题为难解问题。
创建 N、N³、N⁵、N¹⁰、1.1N、2N、N! 的对数对数比例图,如 Harel 第 74 页所示。
随着程序员对计算的经验增加,人们逐渐意识到多项式时间算法是有用的,而指数时间算法则不是。在一篇非常有影响力的论文中,Jack Edmonds 将多项式算法称为“好算法”,并认为多项式时间是高效计算的一个很好的替代。Kurt Godel 在 1956 年给 von Neumann 写了一封信(第 9 页),其中包含了多项式性是一个可取特征的(隐含)概念。早在 1953 年,von Neumann 就认���到了多项式和指数算法之间的定性差异。根据多项式和指数时间对问题进行分类的想法深刻地改变了人们对计算问题的看法。
NP。
非正式地,我们将搜索问题定义为一个计算问题,我们在(可能巨大的)可能性中寻找解决方案,但是当我们找到解决方案时,我们可以轻松检查它是否解决了我们的问题。给定搜索问题的一个实例 I(指定问题的一些输入数据),我们的目标是找到一个解决方案 S(符合某些预先指定标准的实体)或报告不存在这样的解决方案。为了成为搜索问题,我们要求很容易检查 S 是否确实是一个解决方案。在这里,我们指的是在输入 I 的大小上是多项式时间。复杂性类NP是所有搜索问题的集合。以下是一些例子。
-
*线性方程组。*给定线性方程系统 Ax = b,找到满足方程的解 x(如果存在)。这个问题属于 NP,因为如果我们得到一个所谓的解 x,我们可以通过将 x 代入并验证每个方程来检查 Ax = b。
-
*线性规划。*给定线性不等式系统 Ax ≤ b,找到满足不等式的解 x(如果存在)。这个问题属于 NP,因为如果我们得到一个所谓的解 x,我们可以通过将 x 代入并验证每个不等式来检查 Ax ≤ b。
-
*整数线性规划。*给定线性不等式系统 Ax ≤ b,找到满足不等式的二进制(0/1)解 x(如果存在)。这个问题属于 NP,因为如果我们得到一个所谓的解 x,我们可以通过将 x 代入并验证每个不等式来检查 Ax ≤ b。
虽然检查对这三个问题的提议解决方案很容易,但是从头开始找到解决方案有多困难?
备注:我们对 NP 的定义略有不同。在历史上,复杂性类别是根据决策问题(是-否问题)来定义的。例如,给定矩阵A和向量b,是否存在解x使得Ax = b?
P。
复杂性类 P 是所有可以在多项式时间内解决的搜索问题的集合(在确定性图灵机上)。与以前一样,我们根据搜索问题(而不是决策问题)来定义 P。它涵盖了我们可以在实际机器上解决的大多数问题。以下列出了一些例子:
| 问题 | 描述 | 算法 | 实例 | 解决方案 |
|---|---|---|---|---|
| GCD | 找到两个整数 x 和 y 的最大公约数。 | 欧几里得算法(欧几里得,公元前 300 年) | 34, 51 | 17 |
| STCONN | 给定图 G 和两个顶点 s 和 t,找到从 s 到 t 的路径。 | BFS 或 DFS(Theseus) | ||
| SORT | 找到将元素按升序排列的排列。 | 归并排序(冯·诺伊曼,1945) | 2.3 8.5 1.2 9.1 2.2 0.3 | 5 2 4 0 1 3 |
| PLANARITY | 给定一个图 G,在平面上画出它,使得没有两条边相交。 | (Hopcroft-Tarjan, 1974) | ||
| LSOLVE | 给定矩阵 A 和向量 b,找到一个向量 x 使得 Ax = b。 | 高斯消元(Edmonds, 1967) | x+y=1 2x+4y=3 | x = 1/2 y = 1/2 |
| LP | 给定矩阵 A 和向量 b,找到一个向量 x 使得 Ax ≤ b? | 椭球算法(Khachiyan, 1979) | x+y≤1 2x+4y≤3 | x = 0 y = 0 |
| DIOPHANTINE | 给定一个具有整数系数的(稀疏)一元多项式,找到一个整数根? | (Smale 等,1999) | x⁵ - 32 | x = 2 |
扩展的丘奇-图灵论断。
在 1960 年代中期,Cobham 和 Edmonds 独立观察到,在一个广泛的计算模型范围内,可以在多项式步骤内解决的问题集保持不变,从确定性图灵机到 RAM 机。扩展的丘奇-图灵论题断言图灵机与任何物理计算设备一样高效。也就是说,P 是在这个宇宙中可以在多项式时间内解决的搜索问题的集合。如果某个硬件解决了大小为 N 的问题,时间为 T(N),扩展的丘奇-图灵论题断言确定���图灵机可以在时间 T(N)^k 内解决它,其中 k 是某个固定常数,k 取决于特定问题。Andy Yao 表达了这个论题的广泛含义:
它们暗示,至少从原理上讲,要使未来的计算机更加高效,只需要专注于改进现代计算机设计的实现技术。
换句话说,任何合理的计算模型都可以在(概率性)图灵机上高效模拟。对于所有已知的物理通用计算机,扩展的丘奇-图灵论题都是成立的。对于随机访问机器(例如您的 PC 或 Mac),常数 k = 2。因此,例如,如果随机访问机器可以在时间 N^(3/2)内执行计算,则图灵机可以在时间 N³内执行相同的计算。
P = NP 吗?
我们这个时代最深刻的科学问题之一是P = NP。也就是说,所有搜索问题是否都能在多项式时间内解决?Clay Foundation 为解决这个问题提供了100 万美元的千禧奖。以下是一些关于何时解决这个问题的猜测。压倒性的共识是 P != NP,但没有人能够证明。
视频中荷马·辛普森对 P = NP 进行演讲,伴随着《失乐园》的音乐。
哥德尔写给冯·诺伊曼的信预见了 P = NP 问题。他意识到如果 P = NP(可满足性在 P 中),那么“将会有最重要的后果”,因为那时“数学家关于是或否问题的思维工作可以完全被机器取代”。他询问哪些组合问题存在更有效的替代方案以避免穷举搜索。
NP 完全性。
非正式地说,NP 完全问题是 NP 中“最难”的问题;它们最有可能不在 P 中。定义:如果(i)它在 NP 中且(ii)每个 NP 问题都可以多项式归约到它,则问题是NP 完全的。定义 NP 完全性的概念并不意味着这样的问题存在。事实上,NP 完全问题的存在是一件令人惊奇的事情。我们无法通过从每个 NP 问题进行归约来证明问题是 NP 完全的,因为它们有无限多个。在 1960 年代,Cook 和 Levin 证明了 SAT 是 NP 完全的。
这是普遍性的一个例子:如果我们可以解决任何 NP 完全问题,那么我们就可以解决 NP 中的任何问题。独特的科学发现为所有类型的问题提供了共同的解释。更令人惊讶的是,存在着“自然”的 NP 完全问题。
NP 完全性对自然科学的影响是不可否认的。一旦发现了第一个 NP 完全问题,难以解决性质就像“冲击波一样在问题空间中蔓延”,首先是在计算机科学中,然后传播到其他科学学科。帕帕迪米特里奥列出了 20 个不同的科学学科,它们正在应对内部问题。最终,科学家们在意识到他们的核心问题是 NP 完全问题后,发现了它们固有的复杂性。每年有 6000 篇科学论文中提到 NP 完全性作为一个关键词。它“涵盖了计算、科学、数学努力的广泛领域,并似乎粗略地界定了数学家和科学家一直渴望可行计算的范围。”[帕帕迪米特里奥]很少有科学理论有如此广泛和深远的影响。
一些 NP 完全问题。 自从发现 SAT 是 NP 完全以来,已经确定了成千上万个问题是 NP 完全的。1972 年,卡普尔表明离散数学中最臭名昭著的 21 个问题是NP 完全的,包括Tsp,Knapsack,3Color和Clique。科学家未能为这 21 个问题找到有效算法,尽管他们不知道这些问题是 NP 完全的,这是最早表明 P != NP 的证据之一。下面列出了一些 NP 完全问题的样本。这里还有一些NP 完全问题。这只是为了说明它们的多样性和普遍性。
-
Bin Packing. 你有 n 个物品和 m 个箱子。第 i 个物品重 w[i]磅。每个箱子最多可以容纳 W 磅。你能否将所有 n 个物品装入 m 个箱子中,而不违反给定的重量限制?
这个问题有许多工业应用。例如,UPS 可能需要从一个配送中心将大量包裹(物品)运送到另一个中心。它希望将它们放入卡车(箱子)中,并尽可能少地使用卡车。其他 NP 完全变体允许体积要求:每个三维包裹占用空间,你还必须担心如何在卡车内安排包裹。
-
Knapsack. 你有一组 n 个物品。第 i 个物品重 w[i]磅,具有利益 b[i]。你能否选择一些物品的子集,使得总重量小于或等于 W,总利益大于或等于 B?例如,当你去露营时,你必须根据它们的重量和效用选择要带的物品。或者,假设你正在入室行窃,只能在你的背包中携带 W 磅的赃物。每个物品 i 重 w[i]磅,有 b[i]美元的市场价值。你应该偷哪些物品?
-
Subset Sum. 给定 n 个整数,是否存在一个子集,其和恰好为 B?例如,假设这些整数是{4, 5, 8, 13, 15, 24, 33}。如果 B = 36,则答案是 yes(且 4, 8, 24 是一个证明)。如果 B = 14,则答案是 no。
-
Partition. 给定 n 个整数,你能将它们分成两个子集,使得每个子集的和相等吗?例如,假设这些整数是{4, 5, 8, 13, 15, 24, 33}。那么答案是
yes,{5, 13, 33}是一个证明。双处理器的负载平衡。 -
整数线性规划. 给定一个整数矩阵 A 和一个整数向量 b,是否存在一个整数向量 x 使得 Ax ≤ b?这是运筹学中的一个核心问题,因为许多优化问题可以用这种方式表达。请注意,与上面提出的线性规划问题形成对比,我们在这里寻找的是一个有理数向量而不是一个整数向量。可解问题和难解问题之间的界限可能非常微妙。
-
SAT. 给定 n 个布尔变量 x[1],x[2],…,x[N]和一个逻辑公式,是否存在一个真值变量的赋值使得公式是可满足的,即为真?例如,假设公式是
(x[1]’ + x[2] + x[3]) (x[1] + x[2]’ + x[3]) (x[2] + x[3]) (x[1]’ + x[2]’ + x[3]')
然后,答案是 yes,(x[1],x[2],x[3]) = (true,true,false)是一个证书。许多应用于电子设计自动化(EDA),包括测试和验证,逻辑综合,FPGA 布线和路径延迟分析。应用于人工智能,包括知识库推理和自动定理证明。
练习:给定两个电路 C1 和 C2,设计一个新电路 C,使得一些输入值的设置使得 C 输出为真当且仅当 C1 和 C2 等价。
-
3-SAT。 给定 n 个布尔变量 x[1],x[2],…,x[N]和一个逻辑公式(合取范式)的逻辑公式,每个子句恰好有 3 个不同的文字,是否存在一个真值变量的赋值使得公式可满足?
-
团。 给定 n 个人和一组成对友谊关系。是否存在一个由 k 个人组成的团或团,使得团内每对可能的人都是朋友?在绘制友谊图时很方便,其中我们为每个人包括一个节点,并连接每对朋友的边。在以下示例中,n = 11,k = 4,答案是
yes,{2, 4, 8, 9}是一个证书。 -
最长路径。 给定一组节点和节点之间的距离,是否存��一条长度至少为 L 的简单路径连接某对节点?
-
机器调度。 你的目标是在 m 台机器上处理 n 个作业。为简单起见,假设每台机器可以在 1 个时间单位内处理任何一个作业。此外,可能存在优先约束:也许作业 j 必须在作业 k 开始之前完成。你能安排所有作业在 L 个时间单位内完成吗?
调度问题有大量的应用。工作和机器可能相当抽象:为了毕业普林斯顿,你需要修读 n 门不同的课程,但不愿意在任何一个学期修读超过 m 门课程。此外,许多课程有先修课程(在修读 126 之前不能修读 COS 226 或 217,但可以同时修读 226 和 217)。你能在 L 个学期内毕业吗?
-
最短公共超字符串。 给定基因字母表{ a,t,g,c }和 N 个 DNA 片段(例如,ttt,atggtg,gatgg,tgat,atttg),是否存在一个包含 K 个或更少字符的 DNA 序列,其中包含每个 DNA 片段?假设在上面的示例中 K = 11;那么答案是
yes,atttgatggtg是一个证书。应用于计算生物学。 -
蛋白质折叠。 生物体内的蛋白质以非常特定的方式在三维空间中折叠到它们的天然状态。这种几何图案决定了蛋白质的行为和功能。最广泛使用的折叠模型之一是二维亲水-疏水(H-P)模型。在这个模型中,蛋白质是一个由 0 和 1 组成的序列,问题是将其嵌入到一个二维格子中,使得格子中相邻的 1 对数,但不在序列中(它的能量),被最小化。例如,序列 011001001110010 被嵌入到下图中,以便有 5 对新的相邻的 1(用星号表示)。
0 --- 1 --- 1 --- 0* * | 0 --- 1 --- 1 0 | * | | 0 --- 1 * 1 * 1| | |0 0 --- 0最小化蛋白质的 H-P 能量是 NP 难题。(Papadimitriou 等)生物学家普遍认为蛋白质折叠是为了最小化它们的能量。Levinthal 悖论的一个版本问如何可能蛋白质能够有效地解决表面上看起来棘手的问题。
-
积分。 给定整数 a[1],a[2],…,a[N],以下积分是否等于 0?

如果你在下一门物理课程中看到这个积分,你不应该期望能够解决它。这不应该让人感到惊讶,因为在第 7.4 节中,我们考虑了一个不可判定的积分版本。
-
填字游戏. 给定一个整数 N 和一个有效单词列表,是否可以将字母分配给一个 N×N 的网格的单元格,以便所有水平和垂直单词都是有效的?如果一些方格是黑色的,像填字游戏一样,是否更容易?
-
定理. 给定一个假设的定理(比如黎曼猜想),你能否在某种形式系统(如策梅洛-弗伦克尔集合论)中使用最多 n 个符号证明它是真的?
-
俄罗斯方块.
-
扫雷.
-
正则表达式. 给定两个在一元字母表{ 1 }上的正则表达式,它们表示不同的语言吗?给定两个 NFA,它们表示不同的语言吗?也许很难确定这两个问题是否可判定,因为我们没有对一个语言中最小字符串的大小有明显的界限,而不在另一个语言中。[请注意,对于 DFA 的对应不等价问题是多项式可解的。] 我们将问题表述为不等价而不是等价的原因是,通过展示一个字符串 s,很容易检查这两个实体是否不等价。实际上,如果两个语言不同,那么最小字符串在输入大小的多项式中。因此,我们可以使用第 7.xyz 节中的高效算法来检查 s 是否被 RE 识别或被 NFA 接受。然而,要证明两个 RE 等价,我们需要一个保证所有字符串都在另一个中的论证,反之亦然。[可以设计一个(指数级)算法来测试两个 RE 或 NFA 是否等价,尽管这并不明显。]
-
旅鼠. 在游戏旅鼠的一个关卡中,是否可能引导一群绿发旅鼠生物安全到达目的地?
-
单位超立方体上的多项式最小化. 给定 N 个变量的多项式,是否最小值<= C,假设所有变量都在 0 和 1 之间。经典微积分问题:在[0, 1]上,min f(x) = ax² + bx + c。在 x = ??处的导数为 0,但最小值出现在边界处。
-
二次丢番图方程. 给定正整数 a、b 和 c,是否存在正整数 x 和 y,使得 ax² + by = c?
-
结实论. 在三维��形上哪些结实限制了一个 genus ≤ g 的表面?
-
有界后对应问题. 给定一个具有 N 张卡片的后对应问题和一个整数 K &le N,是否存在一个使用最多 K 张卡片的解?请注意,如果 K 没有限制,那么这是不可判定的。
-
纳什均衡. 合作博弈论。给定一个 2 人游戏,找到最大化玩家 1 收益的纳什均衡。是否存在多个 NE?是否存在一个帕累托最优的 NE?最大化社会福利的 NE。
-
二次同余. 给定正整数 a、b 和 c,是否存在一个小于 c 的正整数 x,使得 x² = a (mod b)?
-
3D 中的伊辛模型. 相变的简单数学模型,例如,当水结冰或冷却铁变成磁性时。计算最低能量状态是 NP 难的。如果图是平面的,则可以在多项式时间内解决,但 3D 晶格是非平面的。在被证明 NP 难之前,统计力学的圣杯已经存在了 75 年。建立 NP 完全性意味着物理学家不会再花 75 年时间试图解决不可解的问题。
-
带宽最小化. 给定一个 N×N 矩阵 A 和一个整数 B,是否可以重新排列 A 的行和列,使得 A[ij] = 0,如果|i - j| > B。对数值线性代数很有用。
-
投票和社会选择。 对于个人来说,操纵称为单一可转移选票的投票方案是 NP 难的。在 1876 年,刘易斯·卡罗尔(查尔斯·道奇森)提出的一种方案中,确定谁赢得了选举是 NP 难的。在卡罗尔的方案中,获胜者是通过在选民偏好排名中进行最少的两两相邻变化的候选人成为康德塞特赢家(在两两选举中击败所有其他候选人的候选人)。夏普利-舒比克投票权。计算Kemeny 最优聚合。
应对难解性。
NP 完全性理论表明,除非 P = NP,否则有一些重要问题无法创建同时实现以下三个属性的算法:
-
保证在多项式时间内解决问题。
-
保证解决问题的最优性。
-
保证解决问题的任意实例。
当我们遇到 NP 完全问题时,我们必须放宽三个要求中的一个。我们将考虑解决放宽了三个目标之一的 TSP 问题的解决方案。
复杂性理论处理最坏情况的行为。这留下了设计算法的可能性,这些算法在某些实例上运行速度快,但在其他实例上需要大量时间。例如,Chaff是一个可以解决许多具有 10,000 个变量的实际 SAT 实例的程序。令人惊讶的是,它是由普林斯顿大学的两名本科生开发的。该算法不能保证在多项式时间内运行,但我们感兴趣的实例可能是“简单的”。
有时我们可能愿意牺牲找到最优解的保证。许多启发式技术(模拟退火、遗传算法、Metropolis 算法)已被设计用于找到“几乎最优”的解决方案。有时甚至可以证明最终解决方案的优良程度。例如,Sanjeev Arora 设计了一种近似算法用于欧几里德 TSP 问题,保证找到的解决方案的成本最多比最优解高 1%。设计近似算法是一个活跃的研究领域。不幸的是,也有一些不可近似性结果,即:如果您可以为问题 X 找到一个近似算法,保证可以达到最优解的 2 倍,则 P = NP。因此,为一些 NP 完全问题设计近似算法是不可能的。
如果我们试图解决 TSP 问题的特殊类,例如,点位于圆的边界上或 M×N 格点的顶点上,则我们可以设计高效(且平凡)的算法来解决问题。
利用难解性。 有时难解性问题是一件好事。在第 XYZ 节中,我们将利用难解性问题设计密码系统。
介于 P 和 NP 完全之间。 现在已知大多数 NP 中的自然问题属于 P 或 NP 完全。如果 P != NP,则可以证明有一些 NP 问题既不属于 P 也不属于 NP 完全。就像“我们还没有观察手段的暗物质”。在地下世界中有一些显著的未分类问题:因子分解和子图同构。
-
因子分解。 已知的最佳算法是 2^O(n¹/3 polylog(n)) - 数域筛法。专家认为不属于 P。
-
受限优先级的 3 处理器调度。 给定一组单位长度的任务和一个优先级顺序,在 3 台并行机器上找到最短的调度。
-
转角问题。 给定 N(N-1)/2 个正数(不一定不同),是否存在一组 N 个点在直线上,使得这些数字是 N 个点的两两距离。直觉:点是 I-95 上的出口。问题首次出现在 1930 年代的 X 射线晶体学背景中。在分子生物学中也被称为部分消化问题。
-
布尔公式对偶化。 给定一个单调 CNF 公式和一个单调 DNF 公式,它们是否等价?(a + b)(c + d) = ac + ad + bc + bd。简单地应用德摩根定律会导致指数级算法,因为存在冗余。最佳算法为 O(n^(log n / log log n))。
-
随机游戏。 白色、黑色和自然轮流在有向图的边上移动一个令牌,从起始状态 s 开始。白色的目标是将令牌移动到目标状态 t。黑色的目标是阻止令牌到达 t。自然以随机方式移动令牌。给定一个有向图、一个起始状态 s 和一个目标状态 t,白色是否有一种策略使得令牌到达 t 的概率 ≥ 1/2?该问题属于 NP 交 co-NP,但尚不清楚是否属于 P。人们相信它属于 P,只是我们还没有找到一个多项式时间算法。
其他复杂度类。
复杂度类 P、NP 和 NP-完全是三个最著名的复杂度类。Scott Aaronson 的网站The Complexity Zoo包含了其他复杂度类的全面列表,这些类对问题根据其计算资源(时间、空间、可并行性、随机性使用、量子计算)进行分类。我们在下面描述了一些最重要的类。
-
PSPACE. 复杂度类 PSPACE = 可以使用多项式空间的图灵机解决的问题。PSPACE-完全 = 在 PSPACE 中,且可以在多项式时间内将所有其他问题归约为它。
-
这里是停机问题的一个复杂版本。给定一个被限制在 n 个磁带单元上的图灵机,在最多 k 步内是否会停机?该问题是 PSPACE-完全的,其中 n 以一元编码。这意味着除非 P = PSPACE,否则我们不太可能能够判断一个给定程序在具有 n 个内存单元的计算机上运行是否会在 k 步之前终止,比简单地运行它 k 步并观察发生的情况要快得多。
-
Bodlaender:给定一个具有顶点 1, …, N 的图,两名玩家轮流标记顶点为红色、绿色或蓝色。第一个标记一个与其邻居相同颜色的顶点的玩家失败。确定第一个玩家是否有获胜策略是 PSPACE-完全的。
-
许多传统游戏的变体被证明是棘手的;这在一定程度上解释了它们的吸引力。此外,黑白棋、六角、地理、上海、赛车、五子棋、瞬间疯狂和推箱子的自然推广都是 PSPACE-完全的。
Eppstein 的困难游戏列表。
-
一个给定的字符串是否是上下文敏感文法的成员?
-
两个正则表达式是否描述不同的语言?即使在二进制字母表上也是 PSPACE-完全的,如果其中一个正则表达式是
.*。 -
另一个可以严格化的例子是移动一个复杂对象(例如家具),其附件可以通过不规则形状的走廊移动和旋转。
-
另一个例子出现在并行计算中,当挑战是确定在一个通信处理器系统中是否可能存在死锁状态时。
注意 PSPACE = NPSPACE(Savitch 定理)。
-
-
EXPTIME. 复杂度类 EXPTIME = 所有在确定性图灵机上以指数时间可解决的决策问题。注意 P ⊆ NP ⊆ PSPACE ⊆ EXPTIME,并且根据时间层次定理,至少有一个包含是严格的,但不知道是哪一个(或多个)。有人推测所有包含都是严格的。
-
Harel 的 Roadblock 第 85 页。
-
国际象棋、跳棋、围棋(采用日本式劫争终结规则)和将棋的自然泛化都是 EXPTIME 完全问题。给定一个棋盘局面,第一位玩家能否强迫获胜?这里 N 是棋盘大小,运行时间与 N 呈指数关系。这些问题比奥赛罗(和其他 PSPACE 完全游戏)在理论上更难的一个原因是它们可能需要指数次数的移动。跳棋(在 N×N 棋盘上的英式跳棋):玩家在某一回合可以有指数次数的移动,因为可以进行跳跃序列。[pdf] 注意:根据终结规则的不同,跳棋可能是 PSPACE 完全或 EXPTIME 完全。对于 EXPTIME 完全,我们假设“强制捕获规则”,即如果有可用的跳跃(或跳跃序列),玩家必须进行跳跃。
-
这是停机问题的一个复杂性版本。给定一个图灵机,在最多 k 步内是否会停机?或者,给定一个固定的 Java 程序和一个固定的输入,在最多 k 步内是否会终止?这个问题是 EXPTIME 完全的。这里的运行时间与 k 的二进制表示成指数关系。事实上,没有图灵机可以保证在 O(k / log k)步内解决它。因此,暴力模拟基本上是最佳的方法:可以证明,这个问题不能比运行图灵机的前 k 步并观察发生了什么更快地解决。
一个 EXPTIME 完全问题在确定性图灵机上不能在多项式时间内解决 - 这与 P ≠ NP 猜想无关。
-
-
EXPSPACE. EXPSPACE 完全问题:给定两个“扩展”正则表达式,它们是否表示不同的语言?通过扩展,我们允许一个平方操作(表达式的两个副本)。Stockmeyer 和 Meyer(1973)。或者更简单的集合交集(Hunt,1973)。阿贝尔群的字问题(Cardoza,Lipton,Meyer,1976),向量加法子系统。
向量加法子系统是 EXPSAPCE 难题:给定一个非负向量 s 和一组任意向量 v1、v2、…、vn,如果向量 x 是从 s 可达的,则它要么是(i)向量 s,要么是可达的向量 y + vi,其中 y 是可达的。VAS 问题是确定给定向量 x 是否可达。
-
DOUBLE-EXPTIME. DOUBLE-EXPTIME 类是在双指数时间内可解决的所有决策问题。一个显著的例子是确定first order Presburger arithmetic中的一个公式是否为真。Presburger 算术包括涉及只有+作为操作的整数的语句(没有乘法或除法)。它可以模拟以下语句:如果 x 和 y 是整数,使得 x ≤ y + 2,则 y + 3 > x。1929 年,Presburger 证明了他的系统是一致的(不能证明矛盾,比如 1 > 2)和完备的(每个语句都可以被证明为真或假)。1974 年,Fischer 和 Rabin 证明了任何决定 Presburger 公式真实性的算法都需要至少 2((2(cN)))时间,其中 c 是一个常数,N 是公式的长度。
-
非初等. 对于任何有限的塔,超过 2²²…²N。给定允许平方和补集的两个正则表达式,它们是否描述不同的语言?
其他类型的计算问题。
我们专注于搜索问题,因为这是科学家和工程师非常丰富和重要的问题类别。
-
搜索问题. 这是我们详细考虑的版本。技术上,FP = 多项式时间函数问题,FNP = 非确定性图灵机上的多项式时间函数问题。FP 问题可以有任何可以在多项式时间内计算的输出(例如,两个数字相乘或找到 Ax = b 的解)。
-
决策问题。 传统上,复杂性理论是以是/否问题来定义的,例如,Ax &le b 是否存在解?规约的定义更清晰(无需处理输出)。P 类和 NP 类传统上是以决策问题来定义的。通常搜索问题归约为决策问题(对于所有 NP 完全问题都已知为真)。这样的搜索问题被称为自可归约。P = NP 问题等价于 FP = FNP 问题。
-
全函数。 有时,一个决策问题很容易,而相应的搜索问题(被认为)很难。例如,可能有一个定理断言解肯定存在,但该定理并未提供如何高效找到解的任何提示。
-
子集和示例。给定 N 个数字,找出这些 N 个数字的两个(不相交)子集,使它们的和恰好相等。如果 N = 77,且所有数字最多为二十一位十进制数,则根据鸽巢原理,至少有两个子集的和相等。这是因为有 2⁷⁷ 个子集,但最多有 1 + 77 * 10²¹ < 2⁷⁷ 种可能的和。或者决策 = 复合,搜索 = 因子。
-
约翰·纳什证明了在具有指定效用的两个或更多玩家的正常形式游戏中,纳什均衡总是存在。证明是非构造性的,因此不清楚如何找到这样的均衡。被证明是PPAD-完全 - 已知具有解的问题的 NP-完全问题的类比。
-
广义均衡理论是微观经济学的基础。给定一个有 k 种商品的经济体,每个 N 个代理人都有这些商品的初始禀赋。每个代理人还为每种商品有一个效用函数。阿罗-德布鲁定理断言,在适当的技术条件下(例如,效用函数连续、单调且严格凹),存在一组(唯一的)市场价格,使得每个代理人都卖掉所有商品,并用这笔钱购买最佳组合(即,每种商品的供求平衡)。但市场是如何计算的呢?证明依赖于拓扑学中的一个深刻定理(卡库塔尼不动点定理),目前尚不知道任何有效的算法。经济学家假设市场找到了均衡价格;亚当·斯密用看不见的手的比喻来描述这种社会机制。
-
15-滑块拼图的推广。测试解是否存在在 P 中,但找到最短解是棘手的。[Ratner-Warmuth, 1990]
-
-
优化问题。 有时我们有优化问题,例如,TSP。给定一个 NP 问题和一个解的成本函数,对于给定的实例,目标是找到其最佳解(例如找到最短的 TSP 旅行路线,最小能量配置等)。有时很难表述为搜索问题(找到最短的 TSP 旅行路线),因为不清楚如何有效地检查是否有最优路线。相反,我们重新表述为:给定长度 L,找到长度最多为 L 的旅行路线。然后二分搜索最优 L。
-
计数问题。 给定一个 NP 问题,找出其解的数量。例如,给定一个 CNF 公式,它有多少满足的赋值?包括统计物理和组合数学中的许多问题。从形式上讲,这类问题被称为#P。
-
战略问题。 给定一个游戏,为玩家找到一个最佳策略(或最佳移动)。包括经济学和棋盘游戏中的许多问题(例如,国际象棋,围棋)。
输出多项式时间。
有些问题涉及的输出比单个位的信息更多。例如,输出汉诺塔问题的解至���需要 2^N 步。这个要求不是因为解本质上难以计算,而是因为有 2^N 个输出符号,并且每个输出符号需要一个单位的时间来写入。也许更自然的衡量效率的方法是输入大小和输出大小的函数。一个具有 DFAs 的经典电气工程问题是从 RE 构建一个使用最少状态的 DFA。我们希望的算法在输入 RE 的大小(符号数量)和输出 DFA 的大小(状态数量)上都是多项式的。除非 P = NP,否则设计这样的算法是不可能的。事实上,甚至不可能设计一个在常数(甚至多项式)数量的状态内得出答案的多项式算法!没有 NP 完全性理论,研究人员将浪费时间追随没有前途的研究方向。
其他下界。
-
信息论的。 在第 X.Y 节中,我们看到插入最多使用 N² 次比较来对 N 个项目进行排序,而归并排序最多使用 N log N 次比较。一个自然的问题是我们是否可以做得更好,也许最多使用 5N 次比较,甚至 1/2 N log N 次比较。为了使问题更加明确,我们必须明确陈述我们的计算模型(决策树)。在这里,我们假设我们只通过
less()函数访问数据。由 X 提出的一个引人注目的定理表明,没有(基于比较的)排序算法可以保证在少于 ~ N log N 次比较中对 N 个不同元素的每个输入进行排序。要理解原因,观察到每次比较(调用less)提供一位信息。为了识别正确的排列,您需要 log N! 位信息,而 log N! ~ N log N。这告诉我们,归并排序是(渐近地)最佳的排序算法。不存在任何排序算法(甚至是尚未想象的算法)会使用更少的比较。 -
3-Sum 困难。 给定一组 N 个整数,其中任意三个数相加是否等于 0?存在二次算法(参见练习 xyz),但没有已知的次二次算法。3-SUM 线性归约到计算几何中的许多问题。(查找平面上的点集是否有 3 个共线,决定平面上的线段集是否可以被一条线分成两个子集,确定一组三角形是否覆盖单位正方形,您是否可以将多边形 P 移动到完全位于另一个多边形 Q 内部,机器人运动规划)。
蛮力 TSP 需要 N! 步。使用动态规划,可以将其减少到 2^N。最佳下界 = N。计算复杂性的本质 = 尝试找到匹配的上界和下界。
电路复杂性。
还有其他定义和衡量计算复杂性的方法。具有 n 个输入的布尔电路可以计算 n 个变量的任何布尔函数。我们可以将电路输出 1 的大小为 n 的二进制字符串集合与语言中的字符串集合相关联。我们需要一个用于每个输入大小 n 的电路。Shannon(1949)提出了电路大小作为复杂性的度量。已知,如果语言在 P 中,则语言具有均匀多项式电路。
物理和模拟计算。
P = NP 问题是关于图灵机和经典数字计算机能力的数学问题。我们也可以思考模拟计算机是否也是如此。模拟 意味着任何“确定性物理设备,使用固定数量的物理变量来表示每个问题变量。” 内部状态由连续变量而非离散变量表示。例如,肥皂泡沫,蛋白质折叠,量子计算,齿轮,时间旅行,黑洞等。
Vergis, Steiglitz, and Dickinson 提出了强克尔图灵论文的模拟形式:
任何有限的模拟计算机都可以被数字计算机高效模拟,即数字计算机模拟模拟计算机所需的时间受限于模拟计算机使用的资源的多项式函数。
模拟计算机的资源可以是时间、体积、质量、能量、扭矩或角动量。参考:模拟计算的物理学
任何合理的计算模型(例如,不涉及指数并行性)都可以通过图灵机(辅以硬件随机数生成器)在多项式时间内模拟。
参考:斯科特·阿伦森。可以为物理学提供新的见解。有一天,“NP 完全问题的被假定为难以解决可能被视为寻找新物理理论的有用约束”,就像热力学第二定律一样。仍然可以通过实验证伪,但不要浪费时间…
-
肥皂泡。 传说你可以解决斯坦纳树问题。实际上,只能找到一个局部最小值,并且可能需要一段时间才能找到。
-
量子计算。 一种推测性的计算模型 - 量子计算机 - 可能能够在确定性图灵机无法做到的多项式时间内解决一些问题。彼得·肖尔发现了一个用于分解 N 位整数的 N³ 算法,但在经典计算机上已知的最佳算法需要指数时间。同样的想法可能导致在模拟量子力学系统时获得可比较的加速。这解释了量子计算引起的最近激动,因为它可能导致计算的范式转变。然而,量子计算机尚未违反扩展的丘奇-图灵论题,因为我们尚不知道如何构建它们。(难以利用,因为许多量子信息似乎很容易被与外界的相互作用所破坏,即退相干。)此外,仍然有可能有人在经典计算机上发现一个多项式时间算法来分解,尽管大多数专家认为这是不可能的。格罗弗的算法:在 sqrt(N)时间内搜索而不是 N。
理查德·费曼在 1982 年表明,经典计算机无法模拟量子力学系统而不会指数级减速(争论的关键在于图灵机具有局部性,而量子力学包括“利用远距作用”)。量子计算机可能能够解决这个问题。费曼关于建造一个模拟物理的计算机的引用…
“我想要的模拟规则是,用于模拟大型物理系统所需的计算机元素数量仅与物理系统的时空体积成正比。我不想出现爆炸。”
用“受限于”替换“与…成正比”来重新表述现代复杂性理论。
德乔萨提出的算法在量子计算机上的运行速度被证明比确定性图灵机快得多。(尽管如果图灵机可以访问硬件随机数生成器并且可以以可忽略的概率出错,指数差距就不存在。量子计算机可以生成真正的随机性。)
素数和合数。
通过提供一个因子很容易说服某人一个数字是合数。然后,这个人只需通过长除法检查你是否对他们撒谎。马林·梅森猜想形如 2^p - 1 的数字对于 p = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 和 257 是素数。他对 p = 67 的猜想在两百五十多年后的 1903 年被 F·N·科尔推翻。根据 E·T·贝尔的书籍数学:科学的女王和仆人
在 AMS 的十月会议上,Cole 宣布了一个关于“大数的因式分解”的讲座。他默不作声地走到黑板前,手算出了 2⁶⁷ 的值,仔细地减去 1。然后他将两个数相乘(分别是 193707721 和 761838257287)。黑板上写下的两个结果是相等的。Cole 默默地走回座位,据说这是 AMS 会议中唯一一次观众鼓掌的讲座。没有问题。根据他所说,Cole 花了大约 3 年的每个星期日来找到这个因式分解。
记录上 2⁶⁷ - 1 = 193707721 × 761838257287 = 147573952589676412927。
Q + A
Q. 多项式算法总是有用吗?
A. 不,需要 N¹⁰⁰ 或 10¹⁰⁰ N² 步的算法在实践中与指数算法一样无用。实践中产生的常数通常足够小,使得多项式时间算法适用于巨大问题,因此多项式性通常作为实践中有用的替代品。
Q. 为什么所有搜索问题的类别被命名为 NP?
A. NP 的最初定义是基于非确定性图灵机的:NP 是所有可以在非确定性图灵机上多项式时间内解决的决策问题的集合。粗略地说,确定性和非确定性图灵机之间的区别在于前者像传统计算机一样运行,按顺序执行每个指令,形成一个计算路径;非确定性图灵机可以“分支”,其中每个分支可以并行执行不同的语句,形成一个计算树(如果树中的任何路径导致 YES,则我们接受;如果所有路径导致 NO,则我们拒绝。)这就是 NP 中的 N 来源。事实证明这两个定义是等价的,但现在更广泛使用证书的定义。(此外,Karp 的 1972 年论文使用了多项式时间可验证性的定义。)
Q. 复杂度类 NP-难是什么?
A. 几个竞争性定义。我们定义一个问题(决策、搜索或优化)问题为 NP-难,如果在多项式时间内解决它将意味着 P = NP。定义隐含地使用图灵归约(扩展到搜索问题)。
Q. 在多项式时间内对整数 N 因式分解有什么困难之处 - 我不能只将小于 N(或 √N)的所有潜在因子分成 x 并查看是否有余数为零吗?
A. 算法是正确的,但请记住只需 lg N 位来表示整数 N。因此,为了使算法在输入大小上是多项式的,它必须在 lg N 中是多项式的,而不是 N。
Q. 检查一个整数是否为合数可以在多项式时间内解决,但找到它的因子却未知(或被认为)不可解吗?
A. 有方法证明一个数是合数而不需要得到它的任何因子。数论中的一个著名定理(费马小定理)暗示,如果你有两个整数 a 和 p,使得(i)a 不是 p 的倍数且(ii)a^(p-1) != 1 (mod p),那么 p 不是质数。
Q. 是否存在一个在量子计算机上多项式可解的决策问题,但可以证明不在 P 中?
A. 这是一个未解决的研究问题。FACTOR 是一个候选项,但没有证据表明 FACTOR 不在 P 中,尽管普遍认为它不在 P 中。
Q. NP = EXPTIME 吗?
A. 专家们认为不是,但他们无法证明。
Q. 假设有人证明 P = NP。这将有什么实际后果?
A. 这取决于问题是如何解决的。显然,如果证明 P = NP,那将是一个显著的理论突破。在实践中,如果 P = NP 的证明为一个重要的 NP 完全问题建立了一个快速算法,那可能具有重大意义。如果证明导致旅行商问题的一个 2¹⁰⁰ N¹¹⁷ 的算法(且常数和指数无法减少),那将没有太大的实际影响。也可能有人通过间接手段证明 P = NP,从而根本没有算法!
Q. 假设有人证明 P != NP。这将会有什么实际后果?
A. 这将是一个显著的理论突破,并巩固了计算复杂性的许多基础。
Q. 假设 P = NP。这是否意味着确定性图灵机与非确定性图灵机相同?
A. 不完全是这样。例如,即使 P = NP,非确定性图灵机可能能够在与最佳确定性图灵机相比为 N³ 的时间内解决问题。如果 P = NP,这只是意味着这两种类型的机器在多项式时间内解决相同的决策问题,但它并不说明多项式的次数。
Q. 我在哪里可以了解更多关于 NP 完全性的知识?
A. 权威参考仍然是 Garey 和 Johnson 的《计算机与难解性:NP 完全性理论指南》。许多最重要的后续发现都记录在 David Johnson 的NP 完全性专栏中。
练习
-
假设 X 是 NP 完全的,X 多项式时间归约到 Y,Y 多项式时间归约到 X。那么 Y 是否一定是 NP 完全的?
答案:不是,因为 Y 可能不在 NP 中。例如,如果 X = CIRCUIT-SAT,Y = CO-CIRCUIT-SAT,那么 X 和 Y 满足条件,但未知 Y 是否在 NP 中。请注意,答案取决于我们对多项式时间归约的定义(应为图灵归约而不是 Karp 归约)。
-
解释为什么顶点覆盖问题的优化版本不一定是一个搜索问题。
答案:目前似乎没有有效的方法来证明一个所谓的解决方案是最佳的(即使我们可以在问题的搜索版本上使用二分搜索来找到最佳解决方案)。
网络练习
-
子集和。 给定 N 个正整数和一个目标值 V,确定是否存在一个子集,其和恰好为 V。将整数分成 4 个相等的组。通过蛮力法列举和存储每组中的所有子集和。让 A、B、C 和 D 分别表示四个组的子集和。目标是找到整数 a、b、c 和 d,使得 a + b + c + d = V,其中 a 在 A 中,b 在 B 中,c 在 C 中,d 在 D 中。现在,使用一个堆来列举 a 在 A 中,b 在 B 中的和。同时,使用另一个堆以递减顺序列举 c 在 C 中,d 在 D 中的和。
-
平方根之和。 两个整数平方根之和之间的最小非零差是多少?给定 n 和 k,找到
| √a1 + √a2 + ... + √ak - √b1 - √b2 - ... - √bk |其中 ai 和 bi 在 0 和 n 之间。例如 r(20, 2) = √10 + √11 - √5 - √18 和 r(20, 3) = √5 + √6 + √18 - √4 - √12 - √12。提示:列举前 n/2 个整数的平方根之和的 2^(n/2) 种可能,并将该集合命名为 A,列举后 n/2 个整数的平方根之和的 2^(n/2) 种可能,并将其命名为 B。现在按排序顺序列举 a 在 A 中,b 在 B 中的和,其中 a 在 A 中,b 在 B 中。寻找差异非常微小的和。
-
划分钻石。 给定 N(大约 36)类 D 钻石,将它们分成两组,使它们的总重量尽可能接近。假设重量是实数(以克拉为单位)。
-
DAG 中的哈密顿路径。 给定一个有向无环图 G,给出一个 O(n+m) 时间复杂度的算法来测试它是否是哈密顿图。提示:拓扑排序。
-
如果假设 P 不等于 NP,从旅行推销员问题是 NP 完全的这一事实中我们可以推断出以下哪些?
-
不存在一个能解决 TSP 问题的任意实例的算法。
-
不存在一个能高效解决 TSP 任意实例的算法。
-
存在一个高效解决任意 TSP 实例的算法,但没有人能找到它。
-
TSP 不在 P 中。
-
所有保证解决 TSP 的算法对于某些输入点族都在多项式时间内运行。
-
所有保证解决 TSP 的算法对于所有输入点族都运行在指数时间内。
答案:(b) 和 (d)。
-
-
如果假设 P 不等于 NP,从 PRIMALITY 在 NP 中但不知道是否 NP 完全这一事实中我们可以推断出以下哪些?
-
存在一个能解决任意 PRIMALITY 实例的算法。
-
存在一个能高效解决任意 PRIMALITY 实例的算法。
-
如果我们找到 PRIMALITY 的一个高效算法,我们可以立即将其用作黑盒来解决 TSP。
答案:我们只能推断 (a),因为所有 P 中的问题都是可判定的。如果 P != NP,那么有些 NP 中的问题既不在 P 中也不是 NP 完全的。PRIMALITY 可能是其中之一(尽管最近已被证明不是)。部分 © 不能被推断,因为我们不知道 PRIMALITY 是否是 NP 完全的。
-
-
以下哪些是 NP 完全的?
-
蛮力 TSP 算法。
-
用于排序的快速排序算法。
-
停机问题。
-
希尔伯特的第十个问题。
答案:无。NP 完全性涉及问题而不是问题的具体算法。停机问题和希尔伯特的第十个问题是不可判定的,因此它们不在 NP 中(所有 NP 完全问题都在 NP 中)。
-
-
假设 X 和 Y 是两个决策问题。假设我们知道 X 可归约到 Y。我们可以推断以下哪些?
-
如果 Y 是 NP 完全的,则 X 也是。
-
如果 X 是 NP 完全的,那么 Y 也是。
-
如果 Y 是 NP 完全的且 X 在 NP 中,则 X 是 NP 完全的。
-
如果 X 是 NP 完全的且 Y 在 NP 中,则 Y 是 NP 完全的。
-
X 和 Y 不能同时是 NP 完全的。
-
如果 X 在 P 中,那么 Y 也在 P 中。
-
如果 Y 在 P 中,那么 X 也在 P 中。
答案:(d) 和 (g)。X 可归约到 Y 意味着如果你有一个能高效解决 Y 的黑盒,你可以用它来高效解决 X。X 不比 Y 更难。
-
-
证明 CIRCUIT-SAT 可归约到 CIRCUIT-DIFF。提示:创建一个具有 N 个输入的电路,总是输出 0。
-
证明 CIRCUIT-DIFF 可归约到 CIRCUIT-SAT。
-
证明 DETERMINANT 在 NP 中:给定一个 N×N 的整数矩阵 A,det(A) = 0 吗?
解法:证书是一个非零向量 x,使得 Ax = 0。
-
证明 FULL-RANK 在 NP 中:给定一个 N×N 的整数矩阵 A,det(A) ≠ 0 吗?
解法:证书是一个 N×N 的逆矩阵 B,使得 AB = I。
-
搜索问题 vs. 决策问题。 我们可以使用相应的决策问题来制定一个搜索问题。例如,找到整数 N 的素因子分解问题可以使用决策问题来制定:给定两个整数 N 和 L,N 是否有一个严格小于 L 的非平凡因子。如果相应的决策问题可在多项式时间内解决,那么搜索问题也可以。为了理解原因,我们可以通过使用不同的 L 值和二分查找来高效地找到 N 的最小因子 p。一旦我们有了因子 p,我们可以对 N/p 重复这个过程。
通常我们可以证明搜索问题和决策问题在运行时间上等价于多项式因子。Papadimitriou(示例 10.8)给出了一个有趣的反例。给定 N 个正整数,它们的和小于 2^N - 1,找到两个和相等的子集。例如,下面的 10 个数字的和为 1014 < 1023。
23 47 59 88 91 100 111 133 157 205
由于 N 个整数的子集(2^N)比 1 到 1014 之间的数字更多,必然存在两个不同的子集具有相同的和。但没有人知道一个多项式时间算法来 找到 这样的子集。另一方面,自然的决策问题在常数时间内是易解的:是否存在两个和相同的数字子集?
-
普拉特素性证书。 证明 PRIMES 属于 NP。使用莱默定理(费马小定理的逆定理),它断言大于 1 的整数 p 是素数当且仅当存在一个整数 x,使得 x^(N-1) = 1 (mod p) 且 x^((p-1)/d) ≠ 1 (mod p) 对于 p-1 的所有素数因子 d 都成立。例如,如果 N = 7919,那么 p-1 的素因子分解为 7918 = 2 × 37 × 107。现在 x = 7 满足 7⁷⁹¹⁸ = 1 (mod 7919),但 7^(7918/2) ≠ 1 (mod 7919),7^(7918/37) ≠ 1 (mod 7919),7^(7918/107) ≠ 1 (mod 7919)。这证明了 7919 是素数(假设你递归地证明了 2、37 和 107 是素数)。
-
佩尔方程。 找到佩尔方程 x² - 92y² = 1 的所有正整数解。解答:(1151, 120), (2649601, 276240),等等。有无穷多解,但每个连续的���大约是前一个解的 2300 倍。
-
佩尔方程。 在 1657 年,皮埃尔·费马向他的同事们提出了以下问题:给定一个正整数 c,找到一个正整数 y,使得 cy² 是一个完全平方数。费马使用了 c = 109。结果表明最小解为 (x, y) = (158,070,671,986,249, 15,140,424,455,100)。编写一个程序 Pell.java,读入一个整数 c,并找到佩尔方程的最小解:x² - c y² = 1。尝试 c = 61。最小解为 (1,766,319,049, 226,153,980)。对于 c = 313,最小解为 ( 3,218,812,082,913,484,91,819,380,158,564,160)。该问题在多项式步数内是无法解决的(作为输入 c 位数的函数),因为输出可能需要指数级的位数!
-
3-COLOR 归约到 4-COLOR。 证明 3-COLOR 多项式归约到 4-COLOR。提示:给定一个 3-COLOR 实例 G,通过向 G 添加一个特殊顶点 x 并将其连接到 G 中的所有顶点,创建一个 4-COLOR 实例 G’。
-
3-SAT 是自可归约的。 证明 3-SAT 是自可归约的。也就是说,给定一个回答任意 3-SAT 公式是否可满足的预言机,设计一个算法可以找到一个满足条件的 3-SAT 公式(假设它是可满足的)。你的算法应在多项式时间内运行,再加上多项式次调用预言机。
-
3-COLOR 是自可归约的。 证明 3-COLOR 是自可归约的。也就是说,给定一个回答任意图 G 是否可 3-染色的预言机,设计一个算法可以对图进行 3-染色(假设它是可 3-染色的)。你的算法应在多项式时间内运行,再加上多项式次调用预言机。
-