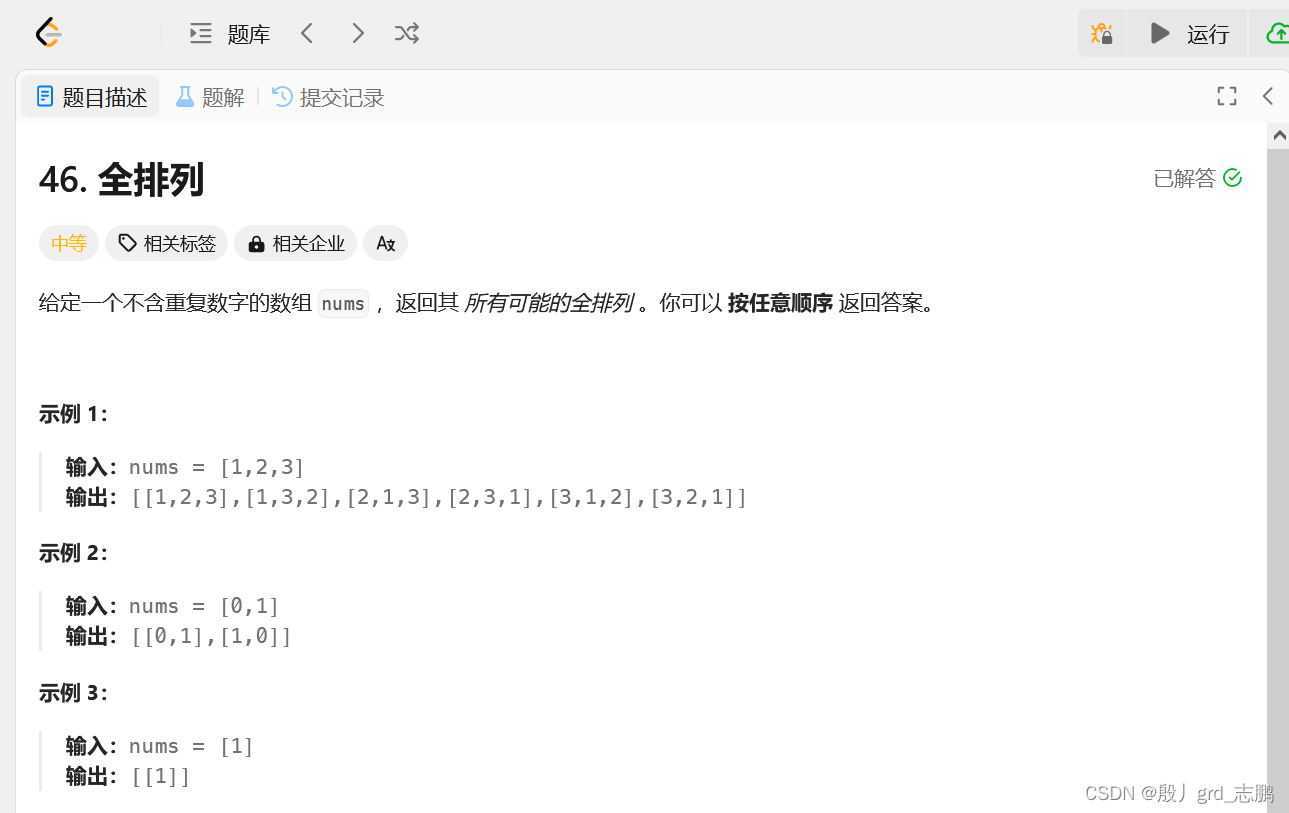
java数据结构与算法刷题目录(剑指Offer、LeetCode、ACM)-----主目录-----持续更新(进不去说明我没写完):https://blog.csdn.net/grd_java/article/details/123063846
暴力回溯 解题思路:时间复杂度O( n n n^n n n n ∗ n ! n*n! n ∗ n !
创建一个flag数组,boolean类型。标志当前数字是否被选过。 我们每个位置的数字枚举时,都先检查flag数组,如果当前数字为false,则可选。 直到所有数字枚举完成
class Solution { int [ ] nums; boolean [ ] numsFlag; int len; List < List < Integer > > = new ArrayList < List < Integer > > ( ) ; public List < List < Integer > > permute ( int [ ] nums) { this . nums = nums; this . len = nums. length; this . numsFlag = new boolean [ len] ; ArrayList < Integer > = new ArrayList < > ( ) ; backTracking ( records) ; return ans; } public void backTracking ( List < Integer > ) { if ( records. size ( ) == len) ans. add ( new ArrayList < > ( records) ) ; else { for ( int i = 0 ; i< len; i++ ) { if ( this . numsFlag[ i] == false ) { this . numsFlag[ i] = true ; records. add ( nums[ i] ) ; backTracking ( records) ; this . numsFlag[ i] = false ; records. remove ( records. size ( ) - 1 ) ; } } } }
}
分区法+回溯 解题思路:时间复杂度O( n ∗ n ! n*n! n ∗ n !
将数组分为两个区域,用index下标分割,index左边保存当前已经选择的数字,右边保存剩余可选的数字 每次通过交换操作,将我们想要在这次选择的数字,移动到index位置,然后index++ 下个数字只能从index和index后面的位置选取。这样就自动跳过了已经选取过的数字。而不用flag数组进行额外的判断
class Solution { List < List < Integer > > = new ArrayList < > ( ) ; int [ ] nums; public List < List < Integer > > permute ( int [ ] nums) { this . nums = nums; backTracking ( 0 ) ; return ans; } public void backTracking ( int index) { if ( index == nums. length) { List < Integer > = new ArrayList < > ( ) ; for ( int num : nums ) list. add ( num) ; ans. add ( list) ; } else { for ( int j = index; j < nums. length; j++ ) { swap ( nums, index, j) ; backTracking ( index + 1 ) ; swap ( nums, j, index) ; } } } private void swap ( int [ ] nums, int i, int j) { if ( i == j) return ; nums[ i] = nums[ i] ^ nums[ j] ; nums[ j] = nums[ i] ^ nums[ j] ; nums[ i] = nums[ i] ^ nums[ j] ; } }