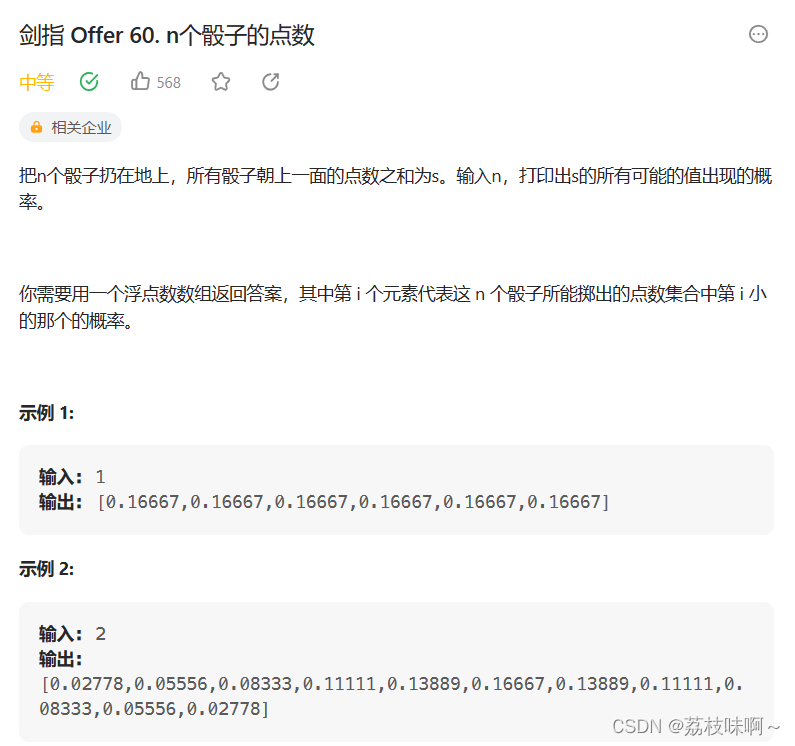
这道题很简单，看完题目就会。看完题就会想到用动态规划的方法，如果我要用i个骰子拿到j个点数，那么我只能在i-1个骰子拿到j-1个点的情况下再用第i个骰子投出一个1，或者i-1个骰子拿到j-2个点的情况下再用第i个骰子投出一个2；.........i-1个骰子拿到j-6个点的情况下再用第i个骰子投出一个6。即dp[i][j]=(dp[i-1][j-1]+dp[i-1][j-2]+dp[i-1][j-3]+dp[i-1][j-4]+dp[i-1][j-5]+dp[i-1][j-6])*1/6。想到这这道题就差不多出来了，n个骰子能投出的最小点是n，最大点是6n，我直接一个二维数组double dp[n+1][6*n+1], dp[i][j]表示用i个骰子投出j个点的概率。其实第i行正真有的是dp[i][i]到dp[i][6i]。但是为了自己理解就直接创建一个[n+1][6*n+1]的数组，然后初始化第1行，也就是用1个骰子能投出的点数的概率，可想而知dp[1][1]到dp[1][6]的概率都是1/6；然后用状态转移公式dp[i][j]=(dp[i-1][j-1]+dp[i-1][j-2]+dp[i-1][j-3]+dp[i-1][j-4]+dp[i-1][j-5]+dp[i-1][j-6])*1/6，但是这样数组会溢出，比如说i等于2，j等于2的时候，j-3=-1会越界，所以我用了一个办法就是把这个公式拆开来，先给dp[i][j]赋初值dp[i][j]=(dp[i-1][j-1]+dp[i-1][j-2])*1/6，如果j>2,就再加上dp[i-1][j-3]*1/6，如果j>3,就再加上dp[i-1][j-4]*1/6......题目需要的是n个骰子投出的概率，需要返回dp[n][n]到dp[n][6*n],所以我们可以再创建一个大小为5*n+1的数组，把dp[n][n]到dp[n][6*n]放进去返回，但是我看错题目了，我以为要把概率从小到大排列，于是我写了一个冒泡排序把数组排一下序再返回，然后一直通过不了，我以为是我的冒泡排序写错了就一直检查冒泡排序，而且我的答案和正确答案差不多，就是我的是两个相同的概率是连在一起的，答案中两个相同的概率是分开的，此时我还没有意识到不用排序，我开始觉得是不是我的dp数组算错了，我就想先不排序，先返回我的dp数组看看是什么样的，于是我把排序那行注释掉了点击提交，卧槽！通过了，我才意识到tm是不是不用排序啊，一看题目才知道人家是点数第i小不是概率第i小。以下是我的代码：

class Solution {public double[] dicesProbability(int n) {double[] res = new double[5*n+1];double[][] dp = new double[n+1][6*n+1];for(int j=1;j<7;j++){dp[1][j]=1.0/6.0;}for(int i=2;i<n+1;i++){for(int j=i;j<6*i+1;j++){dp[i][j] = (dp[i-1][j-1]+dp[i-1][j-2])*1.0/6.0;if(j>2)dp[i][j] += dp[i-1][j-3]*1.0/6.0;if(j>4)dp[i][j] += dp[i-1][j-4]*1.0/6.0;if(j>5)dp[i][j] += dp[i-1][j-5]*1.0/6.0;if(j>6)dp[i][j] += dp[i-1][j-6]*1.0/6.0;}}for(int j = n;j<6*n+1;j++){res[j-n]=dp[n][j];}return res;}
}

看了一下题解，题解还有用一维数组的：

public double[] dicesProbability(int n) {//因为最后的结果只与前一个动态转移数组有关，所以这里只需要设置一个一维的动态转移数组//原本dp[i][j]表示的是前i个骰子的点数之和为j的概率，现在只需要最后的状态的数组，所以就只用一个一维数组dp[j]表示n个骰子下每个结果的概率。//初始是1个骰子情况下的点数之和情况，就只有6个结果，所以用dp的初始化的size是6个double[] dp = new double[6];//只有一个数组Arrays.fill(dp,1.0/6.0);//从第2个骰子开始，这里n表示n个骰子，先从第二个的情况算起，然后再逐步求3个、4个···n个的情况//i表示当总共i个骰子时的结果for(int i=2;i<=n;i++){//每次的点数之和范围会有点变化，点数之和的值最大是i*6，最小是i*1，i之前的结果值是不会出现的；//比如i=3个骰子时，最小就是3了，不可能是2和1，所以点数之和的值的个数是6*i-(i-1)，化简：5*i+1//当有i个骰子时的点数之和的值数组先假定是tempdouble[] temp = new double[5*i+1];//从i-1个骰子的点数之和的值数组入手，计算i个骰子的点数之和数组的值//先拿i-1个骰子的点数之和数组的第j个值，它所影响的是i个骰子时的temp[j+k]的值for(int j=0;j<dp.length;j++){//比如只有1个骰子时，dp[1]是代表当骰子点数之和为2时的概率，它会对当有2个骰子时的点数之和为3、4、5、6、7、8产生影响，因为当有一个骰子的值为2时，另一个骰子的值可以为1~6，产生的点数之和相应的就是3~8；比如dp[2]代表点数之和为3，它会对有2个骰子时的点数之和为4、5、6、7、8、9产生影响；所以k在这里就是对应着第i个骰子出现时可能出现六种情况，这里可能画一个K神那样的动态规划逆推的图就好理解很多for(int k=0;k<6;k++){//这里记得是加上dp数组值与1/6的乘积，1/6是第i个骰子投出某个值的概率temp[j+k]+=dp[j]*(1.0/6.0);}}//i个骰子的点数之和全都算出来后，要将temp数组移交给dp数组，dp数组就会代表i个骰子时的可能出现的点数之和的概率；用于计算i+1个骰子时的点数之和的概率dp = temp;}return dp;}   

当时我看完代码我就有一个疑惑，dp的大小不是6吗，tmp的大小不是5n吗，怎么把一个大的数组赋给一个小的数组呢？搜了一下才明白，当您将一个数组分配给另一个数组变量时，您实际上是将引用分配给该数组，而不是创建新数组或更改数组的大小。因此，当您这样做时dp = tmp，您将dp指向与 相同的数组tmp。结果，循环完成后，dp将保存对数组的引用tmp，并且tmp数组不会丢失或被垃圾回收。