【题目来源】
https://www.acwing.com/problem/content/description/4313/
【题目描述】
给定一棵 n 个节点的树。
节点的编号为 1∼n,其中 1 号节点为根节点,每个节点的编号都大于其父节点的编号。
现在,你需要回答 q 个询问。
每个询问给定两个整数 ui,ki。
我们希望你用 DFS(深度优先搜索)算法来遍历根节点为 ui 的子树。
我们规定,当遍历(或回溯)到某一节点时,下一个遍历的目标应该是它的未经遍历的子节点中编号最小的那一个子节点。
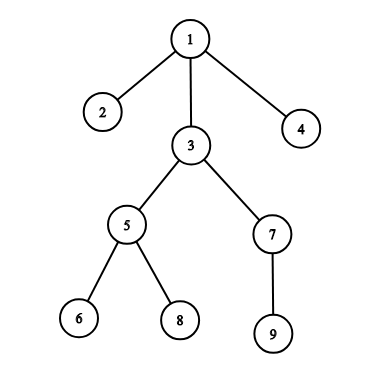
例如,上图实例中:
如果遍历根节点为 1 号节点的子树,则子树内各节点的遍历顺序为 [1,2,3,5,6,8,7,9,4]。
如果遍历根节点为 3 号节点的子树,则子树内各节点的遍历顺序为 [3,5,6,8,7,9]。
如果遍历根节点为 7 号节点的子树,则子树内各节点的遍历顺序为 [7,9]。
如果遍历根节点为 9 号节点的子树,则子树内各节点的遍历顺序为 [9]。
每个询问就是让你计算采用规定的 DFS 算法来遍历根节点为 ui 的子树时,第 ki 个被遍历到的节点的编号。
【输入格式】
第一行包含两个整数 n,q。
第二行包含 n−1 个整数 p2,p3,…,pn,其中 pi 表示第 i 号节点的父节点的编号。
接下来 q 行,每行包含两个整数 ui,ki,表示一组询问。
【输出格式】
共 q 行,每组询问输出一行一个整数表示第 ki 个被遍历到的节点的编号。
如果第 ki 个被遍历到的节点不存在,则输出 −1。
【数据范围】
前三个测试点满足 2≤n≤20,1≤q≤20。
所有测试点满足 2≤n≤2×10^5,1≤q≤2×10^5,1≤pi<i,1≤ui,ki≤n。
【输入样例】
9 6
1 1 1 3 5 3 5 7
3 1
1 5
3 4
7 3
1 8
1 9
【输出样例】
3
6
8
-1
9
4
【算法分析】
﹣注意本例中结点的编号从1开始,所以才有了代码中的dfs(1)。
﹣本题要注意区分结点的编号与树的DFS序列的下标的区别。
﹣for(auto iter:vec)的用法:C++11标准引入了 auto 类型说明符。它通过变量的初始值或者表达式中参与运算的数据类型来推断变量的类型。例如:
#include <bits/stdc++.h>
using namespace std;int main(){string s;cin>>s;for(auto t:s){cout<<t<<endl;}return 0;
} /*
in:
abc123out:
a
b
c
1
2
3
*/-对于一棵树的DFS序列而言,每棵子树的DFS序列对应其中的连续一段。
-树可视为没有环的“有向无权图”。故可借鉴利用STL中的vector实现“有向无权图”的邻接表表示存图的代码实现存树。
/* 利用STL中的vector实现有向无权图的邻接表表示 */
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5;
vector<int> v[N];int main() {int n,m; //n点数,m边数cin>>n>>m;int s,t; //边的邻接点序号,从0开始for(int i=0; i<m; i++) {cin>>s>>t;v[s].push_back(t);// v[t].push_back(s); 与“无向无权图”的邻接表表示相比,就少此行代码}for(int i=0; i<n; i++) {cout<<"V"<<i+1<<":";for(int j=0; j<v[i].size(); j++) {if(j==v[i].size()-1) cout<<v[i][j];else cout<<v[i][j]<<"->";}cout<<endl;}return 0;
}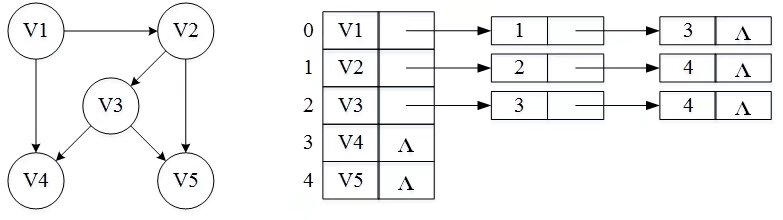
以上关于“有向无权图”的内容解析详见:https://blog.csdn.net/hnjzsyjyj/article/details/101233485
【算法代码】
#include <bits/stdc++.h>
using namespace std;const int maxn=2e5+5;
int val[maxn]; //val[i]存储DFS序列中下标为i的结点在树中的结点编号
int id[maxn]; //id[i]存储结点编号为i的结点在树的DFS序列中的下标
int cnt[maxn]; //cnt[i]存储以结点编号为i的结点为根的子树中的结点数
vector<int> g[maxn];int cur; //树的DFS序列的下标
void dfs(int x){ //x为树的结点编号1~n val[cur]=x;id[x]=cur;cur++;cnt[x]=1;for(auto t:g[x]){dfs(t);cnt[x]+=cnt[t];}
}int main(){int n,m;cin>>n>>m;for(int i=2;i<=n;i++){int t;cin>>t;g[t].push_back(i);}dfs(1);//for(int i=1;i<=n;i++) sort(g[i].begin(),g[i].end());while(m--){int u,k;cin>>u>>k;if(cnt[u]<k) cout<<"-1"<<endl;else cout<<val[id[u]+k-1]<<endl;}return 0;
}/*
in:
9 6
1 1 1 3 5 3 5 7
3 1
1 5
3 4
7 3
1 8
1 9out:
3
6
8
-1
9
4
*/
【参考文献】
https://www.acwing.com/solution/content/97544/
https://blog.csdn.net/Apol1o_/article/details/124563889
https://blog.csdn.net/Jacob0824/article/details/123301752
https://www.acwing.com/solution/content/103008/


![[Docker实现测试部署CI/CD----自由风格和流水线的CD操作(6)]](https://img-blog.csdnimg.cn/ce509b478a244be2a468ad862e9c9a9a.png)