【DL经典回顾】激活函数大汇总（十五）（LogSoftmax附代码和详细公式）-编程知识

激活函数大汇总（十五）（LogSoftmax附代码和详细公式）

更多激活函数见激活函数大汇总列表

一、引言

欢迎来到我们深入探索神经网络核心组成部分——激活函数的系列博客。在人工智能的世界里，激活函数扮演着不可或缺的角色，它们决定着神经元的输出，并且影响着网络的学习能力与表现力。鉴于激活函数的重要性和多样性，我们将通过几篇文章的形式，本篇详细介绍两种激活函数，旨在帮助读者深入了解各种激活函数的特点、应用场景及其对模型性能的影响。

在接下来的文章中，我们将逐一探讨各种激活函数，从经典到最新的研究成果。

限于笔者水平，对于本博客存在的纰漏和错误，欢迎大家留言指正，我将不断更新。

二、LogSoftmax

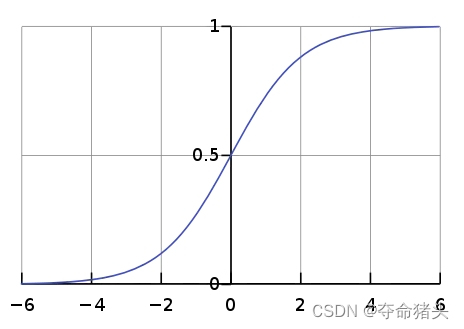
softmax是一个数学函数，它将K个真实的数的向量作为输入，并将其转换为概率分布，参见图，即在应用softmax之前，向量分量可以是负的或大于0，但是在应用softmax之后，每个分量将在区间[0，1]中，这些分量的和等于1，所以我们可以把这些值解释为概率。
在这里插入图片描述

LogSoftmax激活函数是Softmax激活函数的一个变体，常用于深度学习模型中的多分类问题。它结合了Softmax函数的归一化特性和对数运算，经常用于模型的输出层，特别是当模型的输出需要表示为概率对数时。

1. 数学定义

给定一个向量 $z$ ，其元素 $z_i$ 代表模型对第(i)类的原始预测分数（也称为logits），LogSoftmax函数定义为：

$\log \operatorname{Softmax}\left(z_i\right)=\log \left(\frac{e^{z_i}}{\sum_j e^{z_j}}\right)$
其中，分母是对所有类别预测分数的指数求和，确保了输出的归一化，而对数运算则直接提供了概率的对数形式。

2. 函数特性

归一化和稳定性：LogSoftmax通过归一化确保了输出值表示为对数概率，这对于处理极端值特别有用，因为它有助于避免数值计算中的下溢问题。
与Softmax的关系：LogSoftmax可以被看作是对Softmax输出取对数，提供了直接的概率对数输出，这在计算交叉熵损失时非常高效。

3. 导数

LogSoftmax函数的导数相对简单，给定输出类别 $i$ ，其导数为：

$\frac{\partial \log \operatorname{Softmax}\left(z_i\right)}{\partial z_k}= \begin{cases}1-\operatorname{Softmax}\left(z_i\right) & \text { if } i=k \\ -\operatorname{Softmax}\left(z_k\right) & \text { if } i \neq k\end{cases}$
这表示，对于目标类别 $i$ ，梯度取决于该类别的Softmax概率与1的差；而对于非目标类别 $k$ ，梯度为该类别的Softmax概率的负值。

4. 使用场景与局限性

使用场景：

多分类问题：LogSoftmax广泛用于深度学习中的多分类问题，尤其是当模型的输出需要进行概率解释时。
交叉熵损失计算：在使用交叉熵损失函数时，直接使用LogSoftmax作为输出层可以提高计算效率，因为它避免了计算Softmax概率后再取对数的额外步骤。

局限性：

输出解释：由于LogSoftmax提供的是概率的对数形式，直接解释输出可能不如Softmax直观。
数值稳定性：虽然LogSoftmax设计是为了提高数值稳定性，但在实际应用中仍需注意适当的数值处理，以避免数值误差。

5.代码实现

import numpy as npdef log_softmax(x):"""计算LogSoftmax激活函数的值。参数:x -- 输入值，可以是数值、NumPy数组或者多维数组。当处理多维数组时，默认对最后一个维度应用LogSoftmax。返回:LogSoftmax激活后的结果。"""# 防止在指数运算时数值溢出的常见技巧是从输入中减去最大值。# 注意：这里使用keepdims=True保持数组维度不变，以便后续的广播操作。x_max = np.max(x, axis=-1, keepdims=True)# 计算调整后的指数值，并通过指数的总和归一化，得到Softmax概率。# 再对这些概率取对数，得到LogSoftmax值。e_x = np.exp(x - x_max)log_sum_e_x = np.log(np.sum(e_x, axis=-1, keepdims=True))# LogSoftmax实际上是输入的指数减去归一化因子的对数。return (x - x_max) - log_sum_e_x# 示例输入，假设是一批3个样本的logits，每个样本对应3个类别的预测分数。
x = np.array([[2.0, 1.0, 0.1],[1.0, 3.0, 0.2],[0.2, 0.2, 4.0]
])# 应用LogSoftmax激活函数
output = log_softmax(x)print("LogSoftmax Output:\n", output)

解读

数值稳定性：通过从每个输入中减去其最大值（x_max），此技巧有助于避免在进行指数运算时的数值溢出问题，同时不影响最终的结果。这是因为LogSoftmax的计算涉及到比率的对数，而这些比率在减去一个常数后保持不变。
归一化和对数：计算每个元素的指数后，通过其总和对指数进行归一化，得到Softmax的概率分布。然后，对这个归一化的结果取对数，得到最终的LogSoftmax值。这里的(x - x_max) - log_sum_e_x实质上是先对归一化的指数值取对数，再从每个输入减去其对应的最大值和归一化因子的对数。
多维数组支持：通过在np.max和np.sum函数中指定axis=-1和使用keepdims=True，此实现支持对多维数组进行操作，假定最后一个维度是特征或类别维度。这使得函数可以直接应用于一批数据，无需单独处理每个样本。

示例输出解释

对于示例输入，该函数为每个样本的每个类别计算了LogSoftmax值。输出显示了每个类别的LogSoftmax值，这些值可以直接用于计算交叉熵损失，优化多分类问题中的模型性能。

三、参考文献

虽然LogSoftmax函数本身可能不经常作为单独的研究主题出现，但它与Softmax函数和交叉熵损失的讨论密切相关。以下是一些相关的基础文献和资源，这些可以帮助深入理解LogSoftmax函数及其在深度学习中的应用：

Goodfellow, I., Bengio, Y., & Courville, A. (2016). “Deep Learning.” MIT Press. 这本书为深度学习提供了全面的介绍，包括激活函数、损失函数以及如何在神经网络中使用它们的详细讨论。尽管它可能不直接专门讨论LogSoftmax，但提供了对Softmax函数和交叉熵损失的深入讨论，这些都与LogSoftmax紧密相关。
Bishop, C. M. (2006). “Pattern Recognition and Machine Learning.” Springer. Bishop的这本书详细介绍了模式识别和机器学习的基本原理，其中包括分类问题中的概率模型和对数概率的使用。该书通过讨论Softmax函数及其性质，为理解LogSoftmax提供了背景知识。