本节目录
一、带通信号采样定理
1、带通信号采样定理的定义
2、带通信号采样定理的证明
本节内容
一、带通信号采样定理
1、带通信号采样定理的定义
Nyquist采样定理是对频谱分布在(0,fH)上的基带信号的采样分析的,如果信号的频谱分布在某一限定的频带(fL,fH)上,如何对这样的带通信号进行采样?
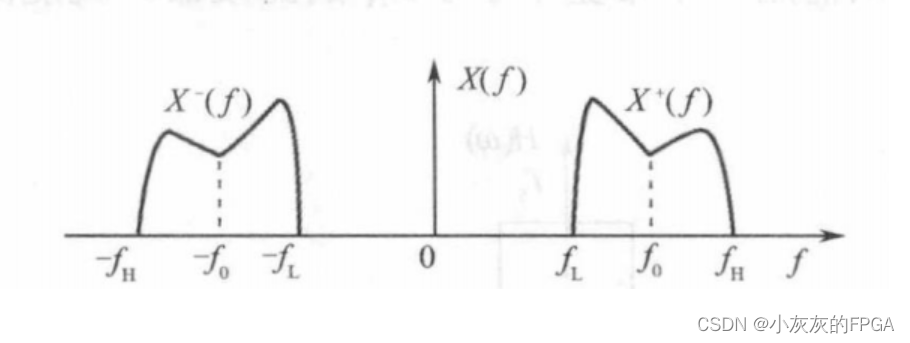
带通采样定理:假设一个频率带限信号x(t),其频带限制在(fL,fH)内,若其采样速率fs=2(fL+fH)/(2n+1),其中n取能满足fs≥2(fH-fL)的最大正整数,则用fs进行等间隔采样所得到的信号采样值x(nTs)能准确地确定原信号x(t)。
由于带通信号的中心频率f0=1/2× (fL+fH),频带宽度B=(fH-fL),故带通采样定理可以表述为:假设一个频率带限信号x(t),其频带限制在(fL,fH)内,若其采样速率fs与中心频率f0满足下述关系式,f0=[(2n+1)/4]×fs,其中n取能满足fs≥2B的最大正整数,则用fs进行等间隔采样所得到的信号采样值x(nTs)能准确地确定原信号x(t)。
如果频带带宽B一定,为了满足最低采样速率fs=2B,也就是两倍频带带宽的采样速率,对于带通信号的中心频率f0的要求是f0=[(2n+1)/4]fs=[(2n+1)/2]×B,或者(fL+fH)=(2n+1)×B,通俗点讲就是信号的最高或最低频率是带宽的整数倍。
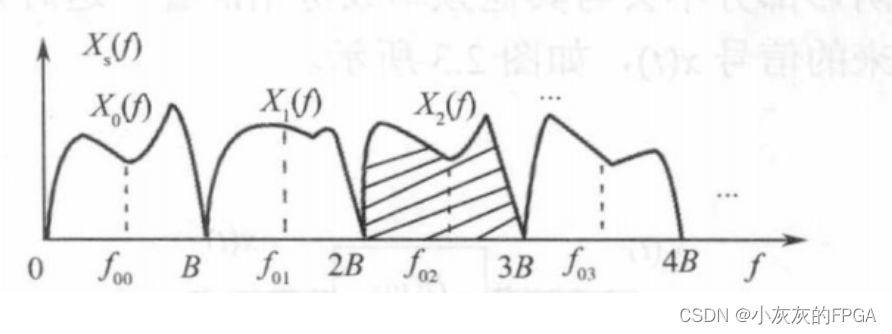
对于上述图形中,任何一个中心频率fon,其中n为正整数,带宽为B的带通信号,均可以用通用的采样频率fs=2B对信号采样,采样离散值均能准确地表示位于不同中心频率的频段对应的原始信号x0(t),x1(t),x2(t)等。满足f0=[(2n+1)/2]×B,且采样频率为2倍带宽的采样称为整带采样。
如何在实际中使用带通采样定理?带通采样定理是否存在前提条件?
当然,带通采样定理只允许在其中一个频带上存在信号,不允许在不同的频带上同时存在信号,否则会引起信号混频。比如上述中阴影部分存在信号,那么其他任何频带上就不能同时存在信号。但是,实际中带通信号并不确定,因此引入了跟踪滤波器,用来满足这样的前提条件。
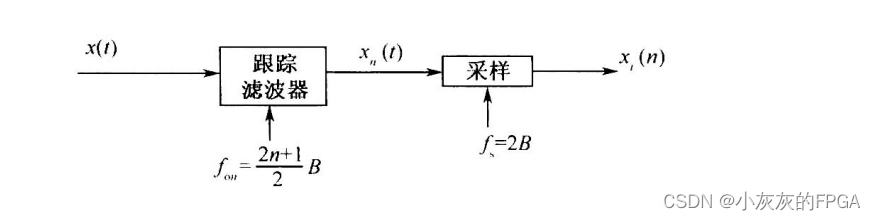
跟踪滤波器满足前提条件,在采样之前先进行滤波,需要对某一中心频率的带通信号进行采样时,先把跟踪滤波器调至与之对应的中心频率f0n上,滤除对应的带通信号xn(t),之后用fs=2B进行采样,从而防止混频。
2、带通信号采样定理的证明
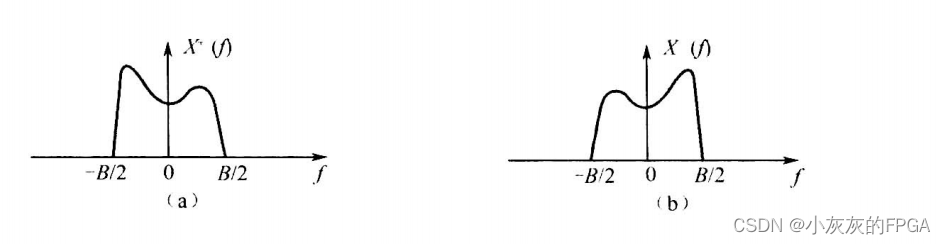
上图中对应的是一个实信号的频谱,具有共轭对称性,也就是说实信号的正负频率幅度分量时对称的,相位分量相反。用X+(f)和X-(f)表示带通信号正负频率分量所对应的两个低通信号,中心频率为f0的带通信号为X(f)=X+(f-f0)+X-(f+f0)。
带通信号的采样频谱Xs(f)=Xs+(f)+Xs-(f),其中Xs+(f)和Xs-(f)为:
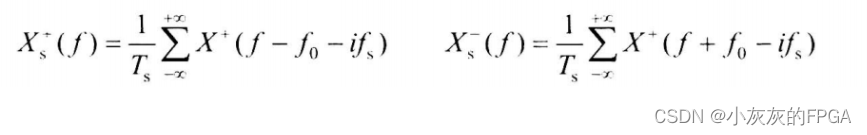
为了确保Xs+(f)和Xs-(f)的频谱不混叠,需要对f0和fs进行限制,提高采样率fs,使得Xs+(f)的空隙部分至少能够容纳Xs-(f),并通过限定f0使Xs-(f)的频谱正好位于Xs+(f)的空隙的中心位置。
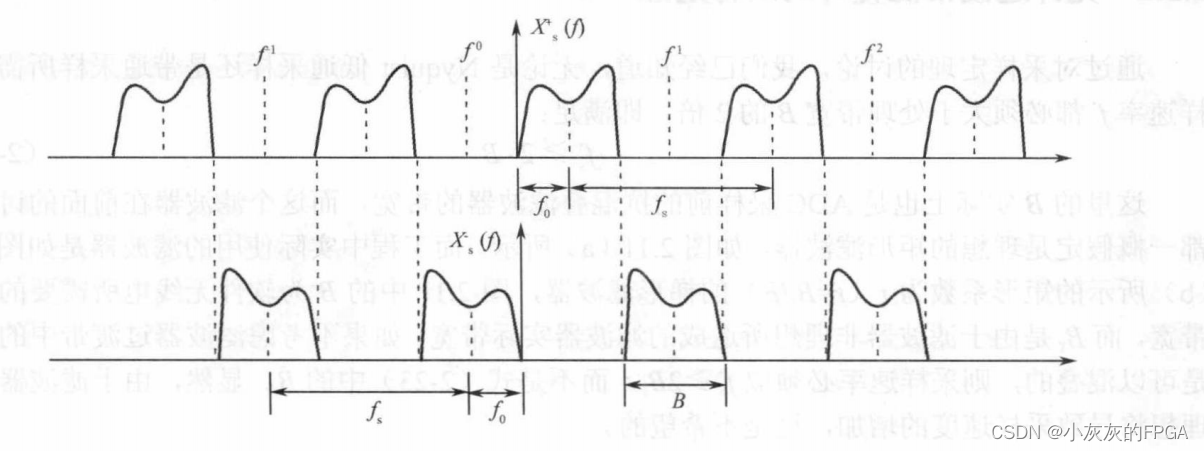
从上图中可以看出fs需要满足的条件是:fs≥2B,也就是采样速率必须大于采样带宽的2倍。
对于Xs+(f)的空隙的中心频率fk=f0-fs/2+k×fs,Xs-(f)的中心频率fi=-f0+i×fs,必须保证Xs-(f)的信号频谱正好位于Xs+(f)的空隙的中心位置,即fk=fi,那么f0=((2(i-k)+1)/4)×fs,也就是f0=[(2n+1)/4]×fs。