一类动态车辆路径问题模型和两阶段算法

摘要

针对一类动态车辆路径问题，分析4种主要类型动态信息对传统车辆路径问题的本质影响，将动态车辆路径问题(Dynamic Vehicle Routing Problem, DVRP)转化为多个静态的多车型开放式车辆路径问题(The Fleet Size and Mixed Open Vehicle Routing Problem, FSMOVRP)，并进一步转化为多个带能力约束车辆路径问题(Capacitated Vehicle Routing Problem, CVRP)，基于CVRP模型建立了DVRP模型；然后，在分析DVRP问题特点基础上，提出两阶段算法，1️⃣第一阶段基于利用K-d trees对配送区域进行分割的策略，提出了复杂度仅为O(nlogn)的快速构建型算法，2️⃣第二阶段通过分析算法搜索解空间结构原理，设计混合局部搜索算法；最后，基于现有12个大规模CVRP标准算例，设计并求解36个DVRP算例.求解结果表明了模型和两阶段算法的有效性。

1. 引言

车辆路径问题(Vehicle Routing Problem, VRP)自1959年Dantzig等[1]提出以来一直受到人们的广泛关注，其研究意义毋庸置疑.随着移动通讯(Global System of Mobile communication, GSM)、电子商务(Electronic Commerce, EC)、全球定位系统(Global Positioning System, GPS)和智能交通系统(Intelligence Transport System, ITS)等技术的发展，物流配送企业能够方便地获取顾客状态、交通路况和任务车辆状态等实时信息.因此，基于传统VRP问题考虑配送中实时信息的动态车辆路径问题(Dynamic Vehicle Routing Problem, DVRP)成为热点研究问题.

由 于 DVRP 问 题 的 理 论 和 实 践 意 义 ，自Psaraftis[2,3]在1988年提出DVRP问题以来，很多学者在该领域做了广泛研究[4]，

• 如 Larsen 研究了DVRP 问题的动态程度特征指标的计算方法[5]；
• Brotcorne 等研究了急救车的动态调度问题，其主要考虑新客户的在线出现[6]；
• 随后研究考虑实时交通 信 息 的 DVRP 学 者 还 有 Taniguchi[7] 和Fleischmann [8].Melachrinoudis 考虑了医疗服务的特殊环境对 DVRP 问题的影响，并构建了相应模型[9].
• 在最近2年里，Khouadjia[10]和Ferrucci[11]分别研究了具有动态客户的 DVRP 问题，并提出了相应的求解策略；
• Albareda-Sambola通过研究验证了将DVRP 按时段分割处理的可行性[12]；
  Ghannadpour研究了多目标 DVRP 问题[13].

针对 DVRP 问题，部分国内学者也进行了较为广泛的研究，

• 如郭耀煌等在综述当前DVRP研究现状的基础上[14]，分别研究了DVRP问题的求解策略[15]和模型[16]；
• 刘霞[17]和Hong[18]研究了带时间窗的 DVRP 问题；
• 陈久梅等研究了装卸一体化的 DVRP 问题，并提出了分区求解策略[19].葛显龙研究了联合配送的开放式DVRP问题[20]

综上所述，当前已有部分学者对 DVRP 研究做了较为深入的研究，但当前针对 DVRP 的研究鲜见分析与VRP的本质区别，并且现有求解算法设计强调求解质量，而对算法合并动态事件生成新方案的速度方面考虑较少[4]
.本文通过分析发现，DVRP问题能够转化为多车型开放式车辆路径问题(The Fleet Size and Mixed Open Vehicle RoutingProblem, FSMOVRP)，并进一步转化为经典的能力约束 VRP 问题(Capacitated VRP, CVRP).首先，1️⃣基于经典的CVRP模型，建立了DVRP模型.然后，2️⃣基于模型提出一个有效的两阶段算法，3️⃣并通过设计和求解标准DVRP算例验证了本文模型与算法的有效性.

2 问题建模

2.1 问题分析

DVRP 与传统的静态 CVRP 问题的主要区别是，在配送过程中会出现新的信息，本文称为动态事件.动态事件主要存在4种类型，包括：
(1) 新顾客出现；
(2) 老顾客改变需求；
(3) 交通堵塞或中断；
(4) 配送车辆抛锚.

本文研究的 DVRP 问题除了经典 CVRP 中的假设外还包括：

(1️⃣) 如果是执行配送任务，设配送的货物为同质物品，每辆车均满载后开始执行任务；如果是回收任务，每辆车均空车开始执行任务.
(2️⃣) 仅考虑局部交通中断情况(即局部发生严重的交通堵塞或道路管制问题)，不考虑大面积的交通瘫痪导致无可行方案的情况.
(3️⃣) 车辆在出现抛锚后，在配送周期内不能够完全修理好.

当任何动态事件发生后，基于原有信息所得到的方案在当前情况下可能质量非常低劣甚至不可行，所以需要结合当前信息，对方案重新优化以及时修正方案.求解该问题关键在于，此时已有部分车辆完成部分配送服务，所在位置已不在配送中心.对于这样的车辆重新优化配送路线，等价于起点(终点)不在配送中心的开放式 VRP(OpenVRP, OVRP)问题，并且由于这些车辆已完成部分配送服务，此时服务能力为车辆所剩货物量，因此等 价 于 多 车 型 OVRP 问 题 (The Fleet Size andMixed OVRP, FSMOVRP).FSMOVRP 问题可以进一步转化为CVRP问题，将不在配送中心的车辆起点或终点虚拟为一个顾客，且需求量为当前最大车载量 Q 与当前车型载量之差，并将该虚拟顾客设定为必须第一个(最后一个)接受服务的顾客.如图1(a)、图1 (b)所示为出现新顾客后的一个DVRP问题，转化为一个CVRP问题示意图.

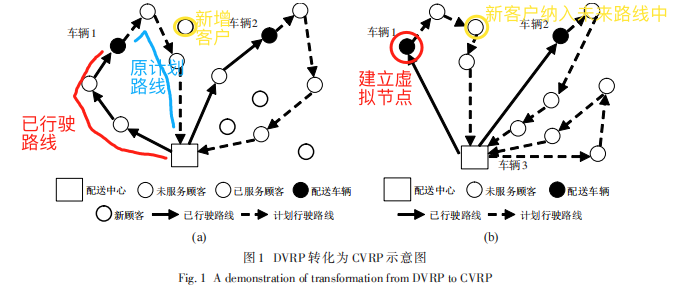
a图是动态的车辆路径问题，b图是静态的有能力约束的车辆路径问题

在a图中，车辆1行驶到黑点的位置，并且经过(红线)了两个节点，按照原来的计划回经过(蓝线)后面两个节点，此时出现了新的请求(黄圈)。把这个问题改建为CVRP,如b图所示，

1. 车辆经过的路线的改进

• 将车辆位置抽象为一个虚拟客户，
• 其需求量=车的最大容载量-当前车型的载量
• 约定为第一个(或最后一个)

2. 新客户的加入

• 可能在原来的计划路线(蓝线)中直接添加客户
• 可能对未服务的节点进行重新规划路线(车辆2计划中额外增加了3个节点，则新增车辆3，与车辆3一起)

同理，对于出现尚未服务的老顾客改变需求和车辆出现抛锚时，通过更新当前尚未服务的顾客可以做类似处理.而当出现交通中断时，相当于求解一个更新顾客间行驶成本后的CVRP问题，在此不再赘述.因此 DVRP 可以转化分解为多CVRP问题。

2.2 数学模型

由以上分析得到，DVRP 可以分解为 (s + 1) 个CVRP问题，可得 DVRP 在时刻点 EventTimei 下的数学规划模型为

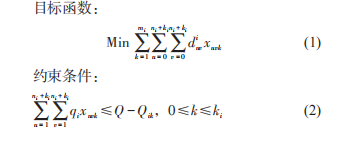
• 式(1)为总行程最小目标；
• 式(2)和式(3)为车载量与行驶距离约束；
• 式(4)和式(5)为计划从配送中心派送车辆的载量与行驶距离约束；
• 式(6)和式(7)表示每个客户恰好仅被 1 辆车服务；
• 式(8)约束了所有车辆的起终点都在配送中心；
• 式(9)表示每辆车行驶的路径轨迹恰好为一个简单圈；
• 式(10)为变量含义和取值；
• 式(11)约束每辆正在执行任务的车辆必须首先服务当前所在位置对应的虚拟顾客，以使配送的路径为简单圈从而由FSMOVRP转化为CVRP问题.
• 式(12)表示动态事件发生的时刻点在配送周期之内，且呈时间序列状态.

3 两阶段算法

根据上述建模思想，求解该模型的最大挑战在于对算法速度有非常高的要求.因为，当动态事件发生的比较频繁时，就要求算法能够在短时间内求解问题.本文设计了一个两阶段算法：改进贪婪算法和混合大邻域算法.采用该两阶段算法求解 DVRP的流程图，如图2所示,

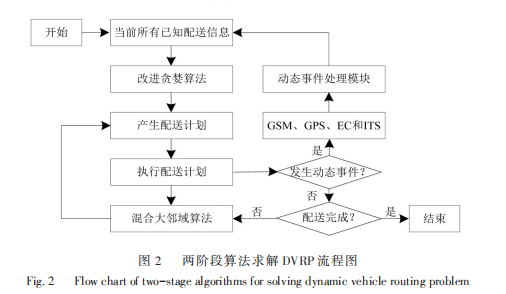如图2图 2 所示，本文求解 DVRP 问题基于“先完
成后完善”的思想.
1️⃣首先采用改进贪婪算法结合新的信息，快速生成一个质量满意的方案；
2️⃣然后充分利用下一个动态事件出现之前的这段时间，采用混合大邻域算法继续改进当前车辆的计划行驶路线；
3️⃣最后，当出现下一个动态事件后再重复这一过程，直到配送过程结束.

3.1 改进贪婪算法

经典贪婪算法(Greedy, GR)求解过程中初期效果非常好，但构造后期会导致质量迅速下降.另外，GR 要求对任意2个顾客形成的距离从小到大排序，那么相当于对 n(n - 1)/2 条边排序，根据排序算法 GR 算法的复杂度至少为 O(n2 log n) ，该复杂度会随着n的增加而迅速增加.本文提出2个分别提高 GR 求解质量和求解速度的策略，得到改进 GR (Improved GR, IMGR).

IMGR 提高质量策略的思想是，让离配送中心较远的边更短，而离配送中心较近的边更长，从而GR将会优先连接离配送中心较远的点，使贪婪算法构造后期质量改进从而提高整体算法的质量；提高速度的策略是，据GR运算原理，其主要计算量为求最邻近点计算，并且实际物流配送中，两点间的路网距离和直线距离高度相关.在此，我们采用K-d trees(K-dimensional binary search trees)法近似求解区域中的最邻近点，本文将配送区域作为2维平面，因此 K = 2 ，其详细执行原理参照Bentley的文献[21].该算法的性能在求解大规模CVRP问题中已得到验证，结合K-d trees的IMGR的求解复杂度仅为 O(nlogn) ，并且求解世界上顾客数量达到20 000的规模最大标准算例的求解质量与理论最优解的偏差仅为5.18%[22]

3.2 混合大邻域算法

通 过 文 献 [23] 研 究 旅 行 商 问 题 (TravelingSalesman Problem, TSP)的求解算法发现，当算法搜索解空间结构(问题解空间中的可行解为节点，互为邻域的可行解之间存在边)类似于小世界网络时，其对应的算法求解质量更优，且只具有某一特定算法规则的算法，其解空间结构更类似于规则网络.

由于 TSP 是 CVRP 的子问题，因此其上述结论对 CVRP 具有一定借鉴意义.根据复杂网络理论可知，多个规则网络混合后得到的网络会更类似于小世界网络[24].因此，多个特定算法规则进行合理混合，就可能得到有效的算法.基于该思想，本文采用改进 CVRP 问题解的 4 种车辆路径间基本规则(Swap、Exchange、Cross-Exchange 和 Inter-relocate)和4种车辆路径中规则(2-opt、Lin-Kernighan、Intrarelocate 和 Or- opt)，设计了一个混合大邻域算法(Hybrid Large Neighborhood Algorithm, HLNA)，其求解规则伪代码如图3所示.

4 算例设计与求解

4.1 算例设计

为了测试本文提出模型和算法的有效性，本文以当前世界上最大的12个CVRP算例[25]为数据基础，按照动态程度δ分别为0.25、0.50和0.75构造36个大规模动态车辆路径问题标准算例，算例中相关参数设定如表1所示.

需要注意的是本文设计的标准算例中只考虑了新顾客出现，其主要原因是
(1) 后 三 种 动 态 事 件 与 当 前 执 行 方 案 密切 相 关 ；
(2)后三种动态事件发生后，根据本文模型也均可以转化为CVRP问题，故在此设计的算例不影响测试本文算法的性能.

表1中设新顾客在整个配送周期中按标号升序方式均匀地出现.

4.2 算例求解

为了对比分析单独使用IMGR(参数α=0.70)和IMGR+HLNA(参数p=0.05)联合使用的效果，本文分别用该两种方式求解在4.1节设计的36大规模
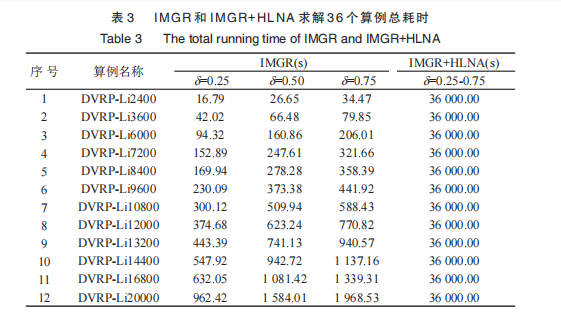
动态车辆路径问题的标准算例，求解环境：StudioVisual C++6.0；CPU 为 Inter® core ™ Q9400，内存为 4.0G，主频为 2.66GHz，其求解质量如表 2所示，求解总耗时如表3所示，需要注意的是，求解质量为求解路径长度与对应静态算例已知最优解的偏差.

由求解结果可知，对于规模相同的算例，动态程度越大IMGR与IMGR+HLNA的求解质量会越差.并且相比较而言，IMGR+HLNA的求解质量要优于IMGR，通过对比表2所示的不同算例相邻动态事件间隔可以发现，动态事件发生的越频繁，IMGR+HLNA 的求解质量优势越不明显，这是因为用于HLNA进一步改进的时间非常紧迫.由上述求解质量结果可以得到以下启示：

1. HLNA是元启发式算法，需要更充足的运行时间才能保证改进IMGR的求解结果，当运行时间非常有限时(不足 60 s)，IMGR+HLNA 与 IMGR几乎有类似的求解结果.
2. IMGR+HLNA 在时间紧迫的情况下对于有些算例的求解质量甚至略低于IMGR(如DVRPLi14400动态程度δ=0.75时)，这说明在动态车辆路径算例中，当前更优的求解结果并不一定会导致最终形成的解质量更高.

由表3所示的 IMGR 和 IMGR+HLNA 的求解总时间可知，IMGR 远远少于 IMGR+HLNA 的求解时间.这是因为 IMGR+HLNA 为了在动态事件未出现时，充分利用 HLNA 不断优化当前未执行的计划配送路线，使 HLNA 在整个配送周期T=10 h=36 000 s中一直处于运行状态.

总体来说，IMGR能够快速地应对动态事件，生成新的方案，且当动态事件出现非常频繁时IMGR 与 IMGR+HLNA 有类似求解质量，但当动态事件出现时间间隔超过1 min时，IMGR+HLNA求解质量明显优于IMGR.

5 研究结论

本文分析了 DVRP 问题中 4 种主要不同类型动态事件对优化问题本质的影响，通过分析得到DVRP问题可以转化为多个FSMOVRP问题，并进一步转化为 CVRP 问题，基于分析结论建立了DVRP 模型.基于先完成后完善的思想，提出了一个由复杂度仅为 O(nlogn) 的 IMGR 和 HLNA 构成的两阶段算法.为了验证本文提出的模型和算法的有效性，基于 12 个当前世界上最大的 CVRP 问题的标准算例，设计了36个DVRP算例，通过求解发现，本文提出的两阶段算法能够在合理时间内，求解动态程度较高的大规模的DVRP问题.