目录
- 第一门课:神经网络和深度学习 (Neural Networks and Deep Learning)
- 第二周:神经网络的编程基础 (Basics of Neural Network programming)
- 2.5 导数(Derivatives)
- 2.6 更多的导数例子(More Derivative Examples)
- 2.7 计算图(Computation Graph)
- 2.8 使用计算图求导数(Derivatives with a Computation Graph)
第一门课:神经网络和深度学习 (Neural Networks and Deep Learning)
第二周:神经网络的编程基础 (Basics of Neural Network programming)
2.5 导数(Derivatives)
这个视频我主要是想帮你获得对微积分和导数直观的理解。或许你认为自从大学毕以后你再也没有接触微积分。这取决于你什么时候毕业,也许有一段时间了,如果你顾虑这点,请不要担心。为了高效应用神经网络和深度学习,你并不需要非常深入理解微积分。因此如果你观看这个视频或者以后的视频时心想:“哇哦,这些知识、这些运算对我来说很复杂。”我给你的建议是:坚持学习视频,最好下课后做作业,成功的完成编程作业,然后你就可以使用深度学习了。在第四周之后的学习中,你会看到定义的很多种类的函数,通过微积分他们能够帮助你把所有的知识结合起来,其中有的叫做前向函数和反向函数,因此你不需要了解所有你使用的那些微积分中的函数。所以你不用担心他们,除此之外在对深度学习的尝试中,这周我们要进一步深入了解微积分的细节。所有你只需要直观地认识微积分,用来构建和成功的应用这些算法。最后,如果你是精通微积分的那一小部分人群,你对微积分非常熟悉,你可以跳过这部分视频。其他同学让我们开始深入学习导数。

一个函数𝑓(𝑎) = 3𝑎,它是一条直线。下面我们来简单理解下导数。让我们看看函数中几个点,假定𝑎 = 2,那么𝑓(𝑎)是𝑎的 3 倍等于 6,也就是说如果𝑎 = 2,那么函数𝑓(𝑎) = 6。假定稍微改变一点点𝑎的值,只增加一点,变为 2.001,这时𝑎将向右做微小的移动。0.001 的差别实在是太小了,不能在图中显示出来,我们把它右移一点,现在𝑓(𝑎)等于𝑎的 3 倍是 6.003,画在图里,比例不太符合。请看绿色高亮部分的这个小三角形,如果向右移动 0.001,那么𝑓(𝑎)增加 0.003,𝑓(𝑎)的值增加 3 倍于右移的𝑎,因此我们说函数𝑓(𝑎)在𝑎 = 2,.是这个导数的斜率,或者说,当𝑎 = 2时,斜率是 3。导数这个概念意味着斜率,导数听起来是一个很可怕、很令人惊恐的词,但是斜率以一种很友好的方式来描述导数这个概念。所以提到导数,我们把它当作函数的斜率就好了。更正式的斜率定义为在上图这个绿色的小三角形中,高除以宽。即斜率等于 0.003 除以 0.001,等于 3。或者说导数等于 3,这表示当你将𝑎右移 0.001,𝑓(𝑎)的值增加 3 倍水平方向的量。
现在让我们从不同的角度理解这个函数。假设𝑎 = 5 ,此时𝑓(𝑎) = 3𝑎 = 15。把𝑎右移一个很小的幅度,增加到 5.001,𝑓(𝑎) = 15.003。 即在𝑎 = 5 时,斜率是 3,这就是表示,当微小改变变量𝑎的值,𝑑𝑓(𝑎)/𝑑𝑎= 3 。一个等价的导数表达式可以这样写 𝑑𝑓(𝑎) /𝑑𝑎,不管你是否将𝑓(𝑎)放在上面或者放在右边都没有关系。
在这个视频中,我讲解导数讨论的情况是我们将𝑎偏移 0.001,如果你想知道导数的数学定义,导数是你右移很小的𝑎值(不是 0.001,而是一个非常非常小的值)。通常导数的定义是你右移𝑎(可度量的值)一个无限小的值,𝑓(𝑎)增加 3 倍(增加了一个非常非常小的值)。也就是这个三角形右边的高度。
那就是导数的正式定义。但是为了直观的认识,我们将探讨右移𝑎 = 0.001 这个值,即使 0.001 并不是无穷小的可测数据。导数的一个特性是:这个函数任何地方的斜率总是等于3,不管𝑎 = 2或 𝑎 = 5,这个函数的斜率总等于 3,也就是说不管𝑎的值如何变化,如果你增加 0.001,𝑓(𝑎)的值就增加 3 倍。这个函数在所有地方的斜率都相等。一种证明方式是无论你将小三角形画在哪里,它的高除以宽总是 3。
我希望带给你一种感觉:什么是斜率?什么是导函数?对于一条直线,在例子中函数的斜率,在任何地方都是 3。在下一个视频让我们看一个更复杂的例子,这个例子中函数在不同点的斜率是可变的。
2.6 更多的导数例子(More Derivative Examples)
在这个视频中我将给出一个更加复杂的例子,在这个例子中,函数在不同点处的斜率是不一样的,先来举个例子:

我在这里画一个函数,𝑓(𝑎) = a 2 a^2 a2,如果𝑎 = 2 的话,那么𝑓(𝑎) = 4。让我们稍稍往右推进一点点,现在𝑎 = 2.001 ,则𝑓(𝑎) ≈ 4.004 (如果你用计算器算的话,这个准确的值应该为 4.004。0.001 我只是为了简便起见,省略了后面的部分),如果你在这儿画,一个小三角形 你就会发现,如果把𝑎往右移动 0.001,那么𝑓(𝑎)将增大四倍,即增大 0.004。在微积分中我们把这个三角形斜边的斜率,称为𝑓(𝑎)在点𝑎 = 2 处的导数(即为 4),或者写成微积分的形式,当𝑎 = 2 的时候, 𝑑𝑓(𝑎)/𝑑𝑎 = 4 由此可知,函数𝑓(𝑎) = 𝑎2,在𝑎取不同值的时候,它的斜率是不同的,这和上个视频中的例子是不同的。
这里有种直观的方法可以解释,为什么一个点的斜率,在不同位置会不同如果你在曲线上,的不同位置画一些小小的三角形你就会发现,三角形高和宽的比值,在曲线上不同的地方,它们是不同的。所以当𝑎 = 2 时,斜率为 4;而当𝑎 = 5时,斜率为 10 。如果你翻看微积分的课本,课本会告诉你,函数𝑓(𝑎) = a 2 a^2 a2的斜率(即导数)为2𝑎。这意味着任意给定一点𝑎,如果你稍微将𝑎,增大 0.001,那么你会看到𝑓(𝑎)将增大2𝑎,即增大的值为点在𝑎处斜率或导数,乘以你向右移动的距离。
现在有个小细节需要注意,导数增大的值,不是刚好等于导数公式算出来的值,而只是根据导数算出来的一个估计值。
为了总结这堂课所学的知识,我们再来看看几个例子:

假设𝑓(𝑎) = a 3 a^3 a3 如果你翻看导数公式表,你会发现这个函数的导数,等于 3 a 2 3a^2 3a2。所以这是什么意思呢,同样地举一个例子:我们再次令𝑎 = 2,所以 a 3 a^3 a3 = 8 ,如果我们又将𝑎增大一点点,你会发现𝑓(𝑎) ≈ 8.012,你可以自己检查一遍,如果我们取 8.012,你会发现2.0013 ,和 8.012 很接近,事实上当𝑎 = 2时,导数值为3 × 2 2 2^2 22,即3 × 4 = 12。所以导数公式,表明如果你将𝑎向右移动 0.001 时,𝑓(𝑎) 将会向右移动 12 倍,即 0.012。
来看最后一个例子,假设𝑓(𝑎) = log𝑒𝑎,有些可能会写作ln𝑎,函数log𝑎 的斜率应该为1/𝑎,所以我们可以解释如下:如果𝑎取任何值,比如又取𝑎 = 2,然后又把𝑎向右边移动 0.001 那么𝑓(𝑎)将增大1/𝑎× 0.001,如果你借助计算器的话,你会发现当𝑎 = 2时𝑓(𝑎) ≈ 0.69315 ;
而𝑎 = 2.001时,𝑓(𝑎) ≈ 0.69365。所以𝑓(𝑎)增大了 0.0005,如果你查看导数公式,当𝑎 = 2的时候,导数值 𝑑𝑓(𝑎) /𝑑𝑎 =1/2。这表明如果你把 增大 0.001,𝑓(𝑎)将只会增大 0.001 的二分之一,即 0.0005。如果你画个小三角形你就会发现,如果𝑥 轴增加了 0.001,那么𝑦 轴上的函
数log𝑎,将增大 0.001 的一半 即 0.0005。所以 1𝑎 ,当𝑎 = 2时这里是 ,就是当𝑎 = 2时这条线的斜率。这些就是有关导数的一些知识。
在这个视频中,你只需要记住两点:
第一点,导数就是斜率,而函数的斜率,在不同的点是不同的。在第一个例子中𝑓(𝑎) =3𝑎 ,这是一条直线,在任何点它的斜率都是相同的,均为 3。但是对于函数𝑓(𝑎) = a 2 a^2 a2 ,或者𝑓(𝑎) = log𝑎,它们的斜率是变化的,所以它们的导数或者斜率,在曲线上不同的点处是不同的。
第二点,如果你想知道一个函数的导数,你可参考你的微积分课本或者维基百科,然后你应该就能找到这些函数的导数公式。
最后我希望,你能通过我生动的讲解,掌握这些有关导数和斜率的知识,下一课我们将讲解计算图,以及如何用它来求更加复杂的函数的导数。
2.7 计算图(Computation Graph)
可以说,一个神经网络的计算,都是按照前向或反向传播过程组织的。首先我们计算出一个新的网络的输出(前向过程),紧接着进行一个反向传输操作。后者我们用来计算出对应的梯度或导数。计算图解释了为什么我们用这种方式组织这些计算过程。在这个视频中,我们将举一个例子说明计算图是什么。让我们举一个比逻辑回归更加简单的,或者说不那么正式的神经网络的例子。
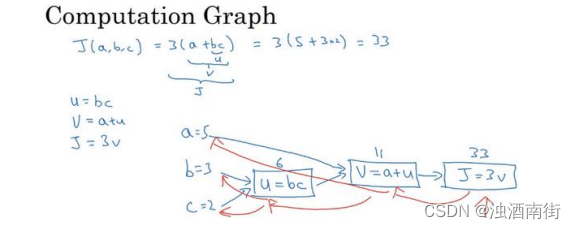
我们尝试计算函数𝐽,𝐽是由三个变量𝑎, 𝑏, 𝑐组成的函数,这个函数是3(a + bc) 。计算这个函数实际上有三个不同的步骤,首先是计算 𝑏 乘以 𝑐,我们把它储存在变量𝑢中,因此𝑢 = 𝑏𝑐; 然后计算𝑣 = 𝑎 + 𝑢;最后输出𝐽 = 3𝑣,这就是要计算的函数𝐽。我们可以把这三步画成如下的计算图,我先在这画三个变量𝑎, 𝑏, 𝑐,第一步就是计算𝑢 = 𝑏𝑐,我在这周围放个矩形框,它的输入是𝑏, 𝑐,接着第二步𝑣 = 𝑎 + 𝑢,最后一步𝐽 =3𝑣。
举个例子: 𝑎 = 5, 𝑏 = 3, 𝑐 = 2 ,𝑢 = 𝑏𝑐就是 6,就是 5+6=11。𝐽是 3 倍的 ,因此。即3 × (5 + 3 × 2)。如果你把它算出来,实际上得到 33 就是𝐽的值。 当有不同的或者一些特殊的输出变量时,例如本例中的𝐽和逻辑回归中你想优化的代价函数𝐽,因此计算图用来处理这些计算会很方便。从这个小例子中我们可以看出,通过一个从左向右的过程,你可以计算出𝐽的值。为了计算导数,从右到左(红色箭头,和蓝色箭头的过程相反)的过程是用于计算导数最自然的方式。
概括一下:计算图组织计算的形式是用蓝色箭头从左到右的计算,让我们看看下一个视频中如何进行反向红色箭头(也就是从右到左)的导数计算,让我们继续下一个视频的学习。
2.8 使用计算图求导数(Derivatives with a Computation Graph)
在上一个视频中,我们看了一个例子使用流程计算图来计算函数𝐽。现在我们看看流程图的描述,看看你如何利用它计算出函数𝐽的导数。
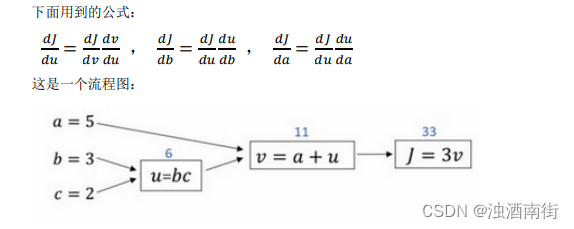
假设你要计算 d J d v \frac{dJ}{dv} dvdJ,那要怎么算呢?好,比如说,我们要把这个𝑣值拿过来,改变一下,那么𝐽的值会怎么变呢?
所以定义上𝐽 = 3𝑣,现在𝑣 = 11,所以如果你让𝑣增加一点点,比如到 11.001,那么𝐽 =3𝑣 = 33.003,所以我这里𝑣增加了 0.001,然后最终结果是𝐽上升到原来的 3 倍,所以 d J d v \frac{dJ}{dv} dvdJ= 3,因为对于任何 𝑣 的增量𝐽都会有 3 倍增量,而且这类似于我们在上一个视频中的例子,我们有𝑓(𝑎) = 3𝑎,然后我们推导出 d d a \frac{d}{da} dad𝑓(𝑎)= 3,所以这里我们有𝐽 = 3𝑣,所以 d J d v \frac{dJ}{dv} dvdJ= 3,这里𝐽扮演了𝑓的角色,在之前的视频里的例子。
在反向传播算法中的术语,我们看到,如果你想计算最后输出变量的导数,使用你最关心的变量对𝑣的导数,那么我们就做完了一步反向传播,在这个流程图中是一个反向步。
我们来看另一个例子, d J d a \frac{dJ}{da} dadJ是多少呢?换句话说,如果我们提高𝑎的数值,对𝐽的数值有什么影响?
好,我们看看这个例子。变量𝑎 = 5,我们让它增加到 5.001,那么对𝑣的影响就是𝑎 + 𝑢,之前𝑣 = 11,现在变成 11.001,我们从上面看到现在𝐽就变成 33.003 了,所以我们看到的是,如果你让𝑎增加 0.001,𝐽增加 0.003。那么增加𝑎,我是说如果你把这个 5 换成某个新值,那么𝑎的改变量就会传播到流程图的最右,所以𝐽最后是 33.003。所以𝐽的增量是 3 乘以𝑎的增量,意味着这个导数是 3。
要解释这个计算过程,其中一种方式是:如果你改变了𝑎,那么也会改变𝑣,通过改变𝑣,也会改变𝐽,所以𝐽值的净变化量,当你提升这个值(0.001),当你把𝑎值提高一点点,这就是𝐽的变化量(0.003)。
首先𝑎增加了,𝑣也会增加,𝑣增加多少呢?这取决于 d v d a \frac{dv}{da} dadv,然后𝑣的变化导致𝐽也在增加,所以这在微积分里实际上叫链式法则,如果𝑎影响到𝑣,𝑣影响到𝐽,那么当你让𝑎变大时,𝐽的变化量就是当你改变𝑎时,𝑣的变化量乘以改变𝑣时𝐽的变化量,在微积分里这叫链式法则。
我们从这个计算中看到,如果你让𝑎增加 0.001,𝑣也会变化相同的大小,所以 d v d a \frac{dv}{da} dadv= 1。事实上,如果你代入进去,我们之前算过 d J d v \frac{dJ}{dv} dvdJ= 3, d v d a \frac{dv}{da} dadv= 1,所以这个乘积 3×1,实际上就给出了正确答案, d J d a \frac{dJ}{da} dadJ= 3。
现在我想介绍一个新的符号约定,当你编程实现反向传播时,通常会有一个最终输出值是你要关心的,最终的输出变量,你真正想要关心或者说优化的。在这种情况下最终的输出变量是𝐽,就是流程图里最后一个符号,所以有很多计算尝试计算输出变量的导数,所以输出变量对某个变量的导数,我们就用𝑑𝑣𝑎𝑟命名,所以在很多计算中你需要计算最终输出结果的导数,在这个例子里是𝐽,还有各种中间变量,比如𝑎、𝑏、𝑐、𝑢、𝑣,当你在软件里实现的时候,变量名叫什么?你可以做的一件事是,在 python 中,你可以写一个很长的变量名,比如𝑑𝐹𝑖𝑛𝑎𝑙𝑂𝑢𝑡𝑝𝑢𝑡𝑣𝑎𝑟_𝑑𝑣𝑎𝑟,但这个变量名有点长,我们就用𝑑𝐽_𝑑𝑣𝑎𝑟,但因为你一直对𝑑𝐽求导,对这个最终输出变量求导。我这里要介绍一个新符号,在程序里,当你编程的时候,在代码里,我们就使用变量名𝑑𝑣𝑎𝑟,来表示那个量。
好,所以在程序里是𝑑𝑣𝑎𝑟表示导数,你关心的最终变量𝐽的导数,有时最后是𝐿,对代码中各种中间量的导数,所以代码里这个东西,你用𝑑𝑣表示这个值,所以𝑑𝑣 = 3,你的代码表示就是𝑑𝑎 = 3。
好,所以我们通过这个流程图完成部分的后向传播算法。我们在下一张幻灯片看看这个例子剩下的部分。
我们清理出一张新的流程图,我们回顾一下,到目前为止,我们一直在往回传播,并计算𝑑𝑣 = 3,再次,𝑑𝑣是代码里的变量名,其真正的定义是 d J d v \frac{dJ}{dv} dvdJ。我发现𝑑𝑎 = 3,再次,𝑑𝑎是代码里的变量名,其实代表 d J d a \frac{dJ}{da} dadJ的值。
同理我们可以计算出
d b = d J d b = d J d v d v d u d u d b = 3 ∗ 1 ∗ c = 3 ∗ 1 ∗ 2 = 6 db=\frac{dJ}{db} =\frac{dJ}{dv} \frac{dv}{du} \frac{du}{db} =3*1*c =3*1*2 =6 db=dbdJ=dvdJdudvdbdu=3∗1∗c=3∗1∗2=6
d c = d J d c = d J d v d v d u d u d c = 3 ∗ 1 ∗ b = 3 ∗ 1 ∗ 3 = 9 dc=\frac{dJ}{dc} =\frac{dJ}{dv} \frac{dv}{du} \frac{du}{dc} =3*1*b =3*1*3=9 dc=dcdJ=dvdJdudvdcdu=3∗1∗b=3∗1∗3=9