元分析_学习笔记-编程知识

1.元分析的基本作用

2.元分析的步骤

2.1文献检索

2.2数据编录

2.3数据分析

3.元分析的基本模型

4.元分析拓展趋势

5.元分析注意事项

6.总结

1.元分析的基本作用

传统作用：针对某一具体的相关关系，对来自不同样本的研究结果进行整合，从而得出对这一关系更为接近样本总体的估计；
新近作用：对某一相关关系在不同样本间的差异进行分析，进而找出能对这些差异进行解释的调节变量；
新近作用：将元分析与其他统计分析方法相结合，对某一变量与其他多个变量直接的整体关系进行分析。

2.元分析的步骤

2.1文献检索

实证研究
尽可能搜索已经发表的
以及已完成但未发表的（发表偏差）
筛选标准：必须是实证研究、必须汇报了样本大小、必须汇报了相关系数或均值差以及能转换成的统计量

2.2数据编录

录入的基本信息：

        ①研究的基本信息（作者姓名、年份、期刊名称等）；

        ②录入者的编码（为保证准确性，至少两名录入者）；

        ③基本数据信息（相关系数、样本大小、标准差、量表信度、量表效度等）；

        ④可能的调节变量（行业、样本类型、变量类型、研究设计等）。

在确定了初步录入模板后，可以随机选取5-10篇文章进行录入，以便发现设计模板时没考虑到的问题。

2.3数据分析

元分析主要是通过对各个实证研究的效应值(量）)(effect size)的分析实现对以往实证研究进行汇总。
效应值是用一个数据统计量来表示某一现象的强度。
在社会科学中，常见的效应值有两种：一是针对两个连续变量的相关系数r；二是实验研究中用来比较两组实验对象的均值差距的d值。

元分析的重点在于文献检索和数据编录。
元分析成果的质量取决于文献检索和数据编录的精细程度。

3.元分析的基本模型

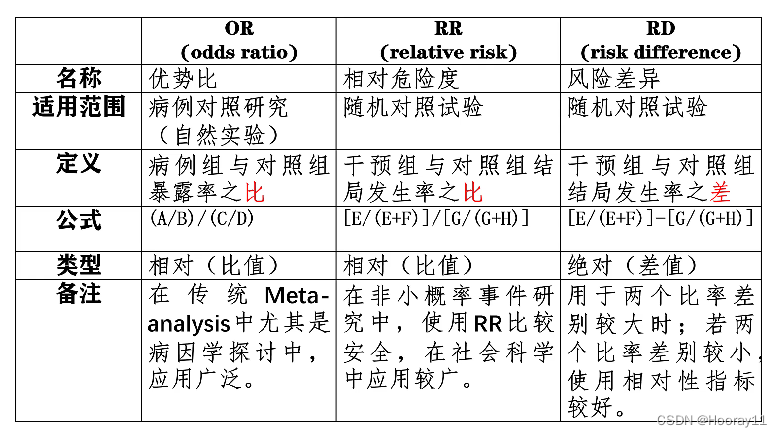
常见的效应值（量）计算指标及其比较

元分析对样本总体的效应值有两种估计模型：

【固定效应模型】该模型假设元分析中所包含的研究都来自同一个样本总体，由于这个总体的平均效应值是固定的，来自这个总体的不同研究所得出的效应值在理论上是同质的；
【随机效应模型】该模型假设元分析中的研究反映不同的样本总体，这些不同的样本总体被看成一个更大的总体的样本，由于这些样本总体的平均效应值是不同的，那么不同研究所得出的效应值在理论上是异质的。
有统计显示，社会科学中的元分析大多采用了随机效应模型。

4.元分析拓展趋势

【拓展趋势一：检验可能影响效应值（量）的调节变量】

        ①Q统计量（Hedges)是对效应值的异质性进行检验的统计量，若Q显著，则意味着效应值可能受到潜在调节变量的影响；

        ②75%法则：如果校正后的效应值方差可以被抽样误差或其他误差所解释的比例低于75%，那么就存在潜在的调节变量；

        ③如果置信区间很宽，包括0，那么也预示着潜在调节变量的存在。

【拓展趋势二：元分析与结构方程模型相结合】

MASEM，包含两个阶段：

第一阶段，通过元分析构建变量之间的相关矩阵或协方差矩阵；
第二阶段，用相关矩阵或协方差矩阵估计结构方程模型。

MASEM的局限：

①普通SEM的协方差矩阵来自同一样本，的矩阵中的数值来自不同的样本，可能导致估计不准确；

②普通SEM基于协方差矩阵进行估计，MASEM使用相关矩阵进行估计，也可能导致估计不准确。

【拓展趋势三：元分析与回归分析相结合】

通过回归方程的形式来比较不同自变量对于因变量影响的相对大小。

5.元分析注意事项

(1）合并同一篇文章中关于同一关系的不同效应值

在编录过程中，如果遇到一篇文章包含了对同一关系的不同效应值，在元分析之前，需要把不同的效应值进行合并，这是因为，这些效应值来自同一样本，它们之间不是独立的。

(2)将意思相近的变量进行归类

有学者将意思相近的变量归入一个大类，进而分析两个含义更广的变量之间的关系。
有学者认为，这样的做法类似于将橘子和苹果放在一起数数，得出的结论没有意义。
也有学者认为，将橘子和苹果合并在一起是有意义的，尤其是关注水果这一大类时。
这两种观点都有道理，关键在于：变量合并的方式是否有理论意义，以及是否与研究问题相符。
在将意义相近的变量合并之前，单独计算它们与某一结果变量之间的加权平均效应值，比较效应值之间是否存在显著的差异，作为辅助证据来支持变量合并。

（3）发表偏差

对发表偏差进行检验的方法：一是文件柜分析，就是估计一下还需要存在多少未发表的研究才能将现有的研究结果从显著变得不显著；二是漏斗图法，漏斗图是使用效应值和样本量作为坐标系，并将各个研究绘制在坐标系中的散点图。其理论依据是，样本量越大，效应量的估计越准确。如果图形呈一个倒着的漏斗形状，则预示着发表偏差可能不存在；如果图形有缺角，则表明发表偏差可能存在。
还可以将发表状态作为一个类别变量，看其对效应值是否有显著的影响，以此判断是否存在潜在的发表偏差。

（4)样本大小

元分析设计两个样本大小：一是元分析所搜集的研究的数量k；二是所有研究所包含的样本总量K。我们希望两个样本数量比较大。
从元分析本身来看，并没有一个绝对的标准来指明需要搜集多少篇关于某一主题的文章才能开始研究。
从现实来看，发表在顶级期刊上元分析研究所搜集的研究的数量差别很大（从50到400都有）。
只要研究者能找到足够大的样本量k对研究问题提供稳定的估计，开展元分析就是有意义的。