目录
选择题
编程题
自除数
除自身以外数组的乘积
选择题
1、下列程序的输出是
#include<stdio.h>
int main()
{int a [12]= {1,2,3,4,5,6,7,8,9,10,11,12},*p[4],i;for(i=0;i<4;i++)p[i]=&a [i*3];printf("%d\n",p[3][2]);return 0;
}- A 上述程序有错误
- B 6
- C 8
- D 12
答案:D
解析:
上述代码中的int* p[4]是指针数组,用于存储指针类型的变量,而因为每个元素都是指针,故可以使用下标解引用操作符p[i],即*(p+i),因为每一个元素的位置存储指针类型的变量,故可以将a数组每个元素的地址存入p数组中,进入for循环后遍历p数组,并将下标为i*3的a数组中的元素的地址存入p数组中,即p[0] = &a[0],p[1] = &a[3],p[2] = &a[6],p[3] = &a[9],而p[3][2],相当于*(*(p+3)+2),即访问p[3]指向位置再向后移动2个int类型大小长度,访问该地址上的数值,即为12
2、二维数组X按行顺序存储,其中每个元素占1个存储单元。若X[4][4]的存储地址为0xf8b82140,X[9][9]的存储地址为0xf8b8221c,则X[7][7]的存储地址为
- A
0xf8b821c4 - B
0xf8b821a6 - C
0xf8b82198 - D
0xf8b821c0
答案:A
解析:
假设每行有n个元素:那x[9][9]元素的地址 - x[4][4]元素的地址 = 0x21c-0x140=5n+5(21c和140是地址末三位的十六进制数,5n+5代表相差5n行5个元素,因为每个元素占1个存储单元,故地址之间的差值即为相差的元素个数),这里n是43,假设x[7][7]的地址是z,x[7][7]元素的地址 - x[4][4]元素的地址 = z-0x140 = 3n+3,z = 3n+3+140 = 3*43+3+0x140 = 0x84+0x140 = 0x1c4,看地址的尾数,选择A

3、以下哪个选项可以正确描述sizeof(double)
- A 一个整型表达式
- B 一个双精度型表达式
- C 一个不合法的表达式
- D 一种函数调用
答案:A
解析:
sizeof是C语言中的一个操作符,不是函数调用,简单的说其作用就是返回一个对象或者类型所占的内存字节数,结果是无符号整数,因此可以把它看作是整型表达式。所以选择A
4、下列代码运行后的结果是什么
int main()
{char a = 'a',b; printf("%c,", ++a); printf("%c\n", b = a++);return 0;
}- A
b,b - B
b,c - C
a,b - D
a,c
答案:A
解析:
变量a里边存的是字符'a',第一次输出先加加再输出,输出的是'b';第二次输出的时候,a先赋值再加加,赋值给b的就是a原来的值,输出b的时候的还是'b'
5、以下逗号表达式的值为
(x = 4 * 5 , x * 5) , x + 5;- A 25
- B 20
- C 100
- D 45
答案:A
解析:
逗号表达式是从前到后依次计算子表达式,而其结果是最后一项的值,此题去掉括号后的表达式,和原表达式是等价的,先计算4*5并赋值给x,x变为20,中间x*5并没有改变x的值,最后一项x+5值是25,也就是整个表达式的值
编程题
自除数
题目链接:728. 自除数 - 力扣(LeetCode)
自除数 是指可以被它包含的每一位数整除的数。
例如,128是一个 自除数 ,因为128 % 1 == 0,128 % 2 == 0,128 % 8 == 0。
自除数 不允许包含 0 。
给定两个整数left和right,返回一个列表, 列表的元素是范围[left, right]内所有的 自除数 。
思路解析:
遍历范围left到right(包括left和right在内)的所有整数,分别判断每个整数是否为自除数。根据自除数的定义,如果一个整数不包含 0且能被它包含的每一位数整除,则该整数是自除数。判断一个整数是否为自除数的方法是遍历整数的每一位,判断每一位数是否为 0 以及是否可以整除该整数。遍历整数的每一位的方法是,每次将当前整数对 10取模即可得到当前整数的最后一位,然后将整数除以 10。重复该操作,直到当前整数变成 0时即遍历了整数的每一位
参考代码
/** @lc app=leetcode.cn id=728 lang=c** [728] 自除数*/// @lc code=start
/*** Note: The returned array must be malloced, assume caller calls free().*/
int *selfDividingNumbers(int left, int right, int *returnSize)
{int *num = (int *)malloc(sizeof(int) * (right - left + 1));(*returnSize) = 0;while (left <= right){int tmp = left; // 确定除数int cal = left % 10; // 确定每一位数int result = 0; // 计算结果int count = 0; // 记录有0出现的次数while (result == 0){// 确保数值中不含有0if (tmp != 0 && tmp % 10 == 0){count++;}// 被除数不能为0if (cal == 0){break;}// 计算结果是否为0result = left % cal;// 取数值的下一位tmp /= 10;cal = tmp % 10;}if (!result && !count){num[(*returnSize)++] = left;}left++;}return num;
}
// @lc code=end除自身以外数组的乘积
题目链接:238. 除自身以外数组的乘积 - 力扣(LeetCode)
给你一个整数数组nums,返回 数组answer,其中answer[i]等于nums中除nums[i]之外其余各元素的乘积 。
题目数据 保证 数组nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请 不要使用除法,且在O(n)时间复杂度内完成此题。
思路解析:
首先本题能直接想到一个思路:将数组的所有元素相乘,再除以当前位置的数值,但是这个思路的问题就是如果除数为0则无法进行,并且题目规定不可以使用除法,所以只能另辟蹊径
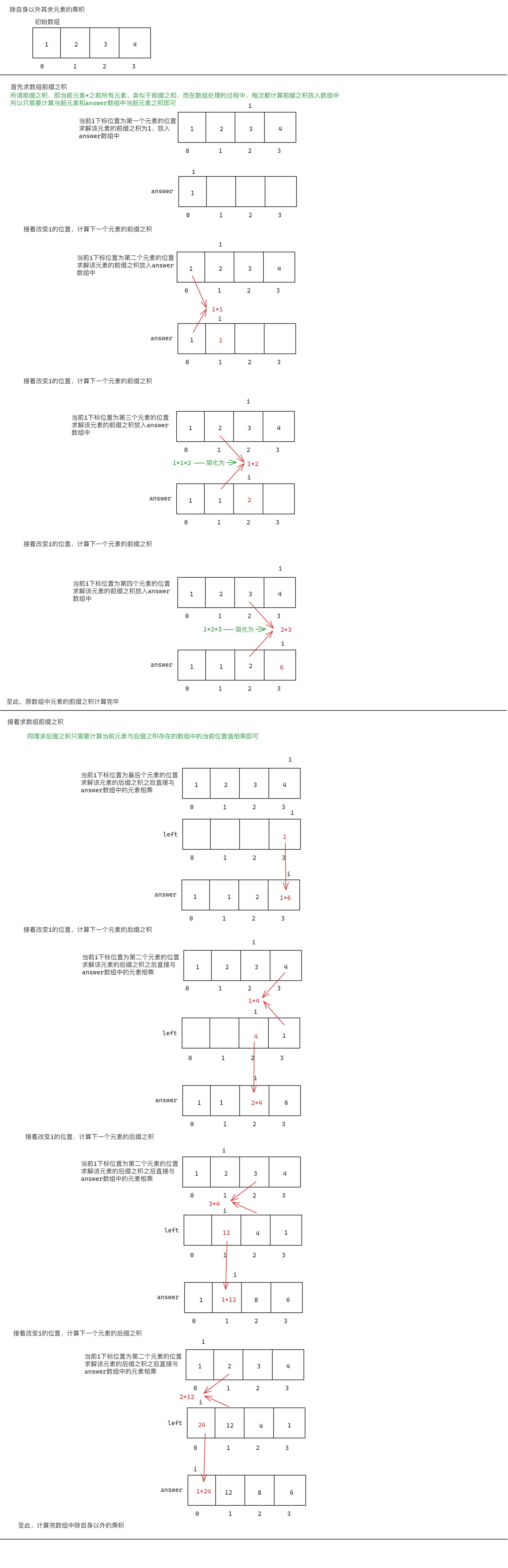
题目中提到“题目数据保证数组 nums之中任意元素的全部前缀元素和后缀的乘积都在32 位整数范围内。”,那么可以考虑先处理数组每个元素的前缀之积,再处理每个元素的后缀之积,因为可以保证前缀之积和后缀之积二者相乘的积不超过int的存储范围,具体思路如下:
需要注意的是,因为前缀之积最后需要与后缀之积相乘故当元素是第一个或最后一个时前缀之积或后缀之积为1
参考代码:
/** @lc app=leetcode.cn id=238 lang=c** [238] 除自身以外数组的乘积*/// @lc code=start
/*** Note: The returned array must be malloced, assume caller calls free().*/
int* productExceptSelf(int* nums, int numsSize, int* returnSize) {int *answer = (int *)malloc(sizeof(int) * numsSize);// 计算数组的前缀之积answer[0] = 1; // 第一个元素的前缀之积为1for (int i = 1; i < numsSize; i++){answer[i] = nums[i - 1] * answer[i - 1];}// 计算后缀之积// 同时将后缀之积与前缀之积相乘int *left = (int *)malloc(sizeof(int) * numsSize);left[numsSize - 1] = 1; // 最后一个元素后缀之积为1for (int i = numsSize - 2; i >= 0; i--){// 先求后缀之积left[i] = left[i + 1] * nums[i + 1];}for (int i = 0; i < numsSize; i++){answer[i] *= left[i];}*returnSize = numsSize;return answer;
}
// @lc code=end