目录
1.程序功能描述
2.测试软件版本以及运行结果展示
3.核心程序
4.本算法原理
5.完整程序
1.程序功能描述
基于最小二乘法的太阳黑子活动模型参数辨识和预测matlab仿真。太阳黑子是人们最早发现也是人们最熟悉的一种太阳表面活动。因为太阳内部磁场发生变化,太阳黑子的数量并不是固定的,它会随着时间的变化而上下波动,每隔一定时间会达到一个最高点,这段时间就被称之为一个太阳黑子周期。太阳黑子的活动呈现周期性变化是由施瓦贝首次发现的。沃尔夫 (R.Wolfer)继而推算出11年的周期规律。实际上,太阳黑子的活动不仅呈11年的周期变化,还有海耳在研究太阳黑子磁场分布时发现的22年周期;格莱斯堡等人发现的80年周期以及蒙德极小期等。由于太阳黑子的活动规律极其复杂,时至今日科学家们仍在努力研究其内在的规律和特性。事实上,对太阳黑子活动规律的研究不仅具有理论意义,而且具有直接的应用需求。太阳黑子的活动呈现周期性变化的,沃尔夫(R.Wolfer)根据在过去的288 年(1700年~1987 年)间每年太阳黑子出现的数量和大小的观测数据推算出11 年的周期规律。我们利用Matlab强大的数据处理与仿真功能,对Wolfer数进行功率谱密度分析从而可以得到对太阳黑子活动周期的结论。
2.测试软件版本以及运行结果展示
MATLAB2022a版本运行

3.核心程序
.................................................................................
ind = 0;
kk=300;
for k=1:length(SSN)+Predict_Len; %开始求K if k <= length(SSN)Y_predict3(k) = c(1,k) + c(2,k)*k + c(3,k)*yc(k) + c(4,k)*ys(k) + c(5,k)*yc2(k) + c(6,k)*ys2(k) + c(7,k)*yc3(k) + c(8,k)*ys3(k); else %Y_predict3(k) = c(1,end) + c(2,end)*k + c(3,end)*yc(k) + c(4,end)*ys(k) + c(5,end)*yc2(k) + c(6,end)*ys2(k) + c(7,end)*yc3(k) + c(8,end)*ys3(k); c0 = mean(c(1,end-kk-1:end-kk));c1 = mean(c(2,end-kk-1:end-kk));c2 = mean(c(3,end-kk-1:end-kk));c3 = mean(c(4,end-kk-1:end-kk));c4 = mean(c(5,end-kk-1:end-kk));c5 = mean(c(6,end-kk-1:end-kk));c6 = mean(c(7,end-kk-1:end-kk));c7 = mean(c(8,end-kk-1:end-kk));Y_predict3(k) = c0 + c1*k + c2*yc(k) + c3*ys(k) + c4*yc2(k) + c5*ys2(k) + c6*yc3(k) + c7*ys3(k); ind = ind + 1;Ys(ind) = Y_predict3(k);end
end
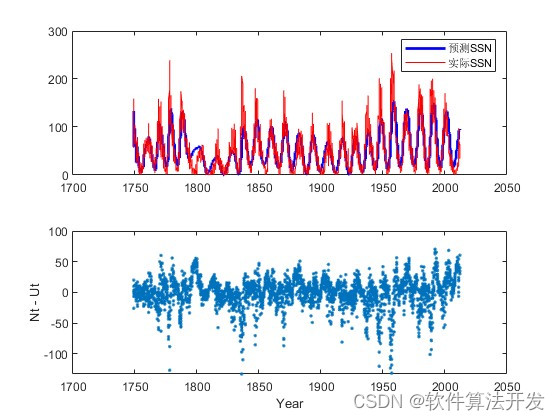
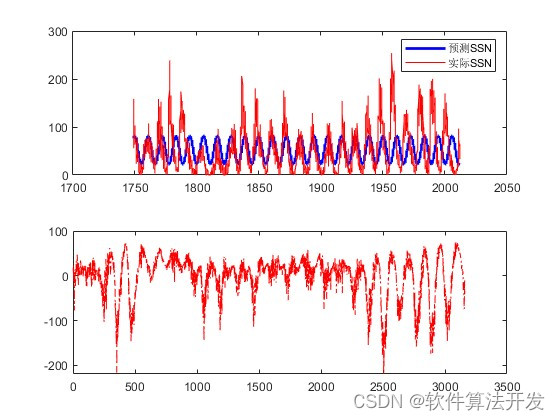
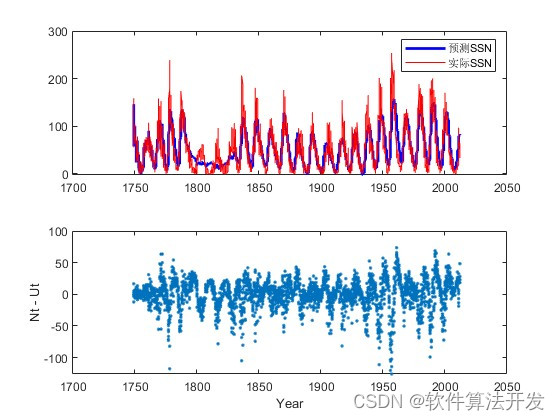
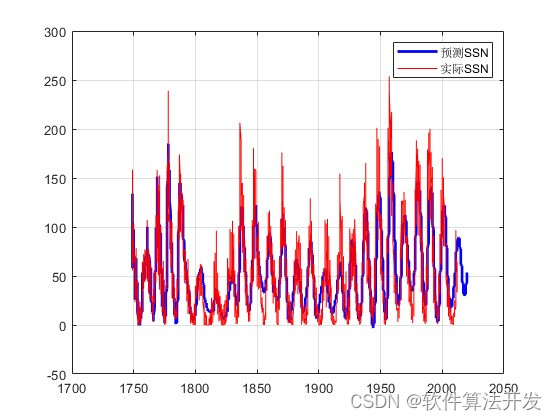
figure;plot(YEAR2,SSN,'r');hold off;
legend('预测SSN','实际SSN');
grid on;%根据预测结果得到下次太阳黑子活动高峰和低峰的时间
%前一次高峰日期为XX = 59;
[Vmax1,Imax1] = max(Ys);
[Vmax2,Imax2] = max(SSN(length(SSN)-XX:length(SSN)));%3100~3160if Vmax1 > Vmax2II = Imax1;MM = Vmax1; time = (length(SSN) + II-3019);%原数据的最后一个月份+预测后的最大值 - 前一个高峰日期
elseII = Imax2;MM = Vmax2; time = (length(SSN) + (XX-II)-3019);%原数据的最后一个月份+预测后的最大值 - 前一个高峰日期
end
Years=time/12;fprintf('下次高峰期日期为:%d',round(2000 + Years));
fprintf('年\n\n');
fprintf('最大值为:%2.2f\n\n\n\n',MM);%计算下一次低谷值
[Vmin,Imin] = min(Ys);
fprintf('下次低峰期日期为:%d',round(2012 + Imin/12));
fprintf('年\n\n');
fprintf('最小值为:%2.2f\n\n',Vmin);
16_013m4.本算法原理
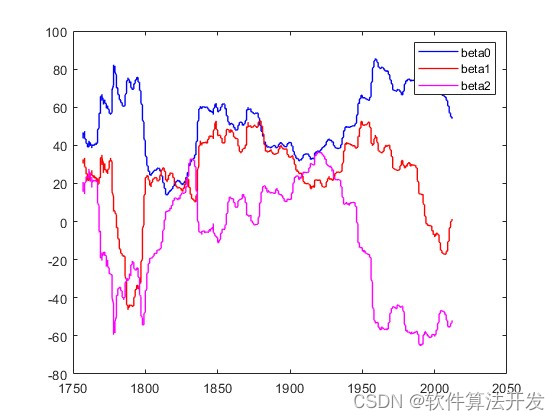
在研究太阳黑子活动时,通常会选择一个合适的物理或统计模型来描述其周期性变化规律。例如,可以选择Hale-Stark定律、Schwabe周期或者某种动力学系统模型等。为了确定模型中的未知参数,我们可以利用历史观测数据采用最小二乘法进行参数辨识。
最小二乘法:
假设我们有一个拟合模型 f(x,θ),其中x 是时间变量,θ=[θ1,θ2,...,θn] 是待估计的模型参数向量。已知一系列太阳黑子活动观测数据yi 对应于时间点 xi (i=1, 2, ..., m),目标是通过调整参数 θ 来使模型输出与实际观测值之间的误差平方和最小。这个优化问题可以用以下数学公式表示:
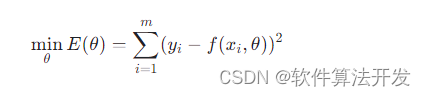
参数辨识步骤:
- 初始化参数:首先为模型参数设定初始值。
- 构建目标函数:根据上述公式构建误差平方和作为目标函数。
- 求解最优参数:运用梯度下降法、牛顿法或其他优化算法找到使目标函数极小化的参数值θ^。
模型预测
一旦通过最小二乘法得到最佳参数估计θ^,就可以使用此参数对未来的太阳黑子活动进行预测:

应用实例 以一个简单的线性模型为例(虽然太阳黑子活动通常具有非线性特征):
![]()
这里的参数向量θ=[θ0,θ1],分别代表截距和斜率。采用最小二乘法就是要找出使得下式最小的 θ0 和θ1:
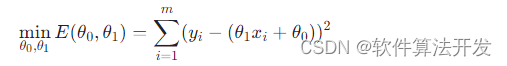
在实际应用中,针对太阳黑子活动这类复杂的自然现象,可能需要选择更高级别的非线性模型,并结合其他科学理论和观测数据进行分析。同时,对于复杂模型,可能会涉及更多优化方法和技术,如正则化最小二乘法以防止过拟合等问题。
5.完整程序
VVV