NeRF学习——NeRF-Pytorch的源码解读-编程知识

学习 github 上 NeRF 的 pytorch 实现项目（https://github.com/yenchenlin/nerf-pytorch）的一些笔记

1 参数

部分参数配置：

训练参数：

这段代码是在设置一些命令行参数，这些参数用于控制NeRF（Neural Radiance Fields）的训练选项。具体来说：
- netdepth：神经网络的层数。默认值为8
- netwidth：每层的通道数。默认值为256
- netdepth_fine：精细网络的层数。默认值为8
- netwidth_fine：精细网络每层的通道数。默认值为256
- N_rand：批量大小（每个梯度步骤的随机光线数）。默认值为 $32 \times 32 \times 4$
- lrate：学习率。默认值为5e-4
- lrate_decay：指数学习率衰减（在1000步中）。默认值为250
- chunk：并行处理的光线数，如果内存不足，可以减少这个值。默认值为1024*32
- netchunk：并行通过网络发送的点数，如果内存不足，可以减少这个值。默认值为1024*64
- no_batching：是否只从一张图像中取随机光线
- no_reload：是否不从保存的检查点重新加载权重
- ft_path：用于重新加载粗网络的特定权重npy文件。默认值为None
- precrop_iters：在中心裁剪上训练的步数。默认值为0。如果这个值大于0，那么在训练的开始阶段，模型将只在图像的中心部分进行训练，这可以帮助模型更快地收敛
- precrop_frac：用于中心裁剪的图像的比例。默认值为0.5。这个值决定了在进行中心裁剪时，应该保留图像的多少部分。例如，如果这个值为0.5，那么将保留图像中心的50%
渲染参数：
- N_samples：每条光线的粗采样数。默认64
- N_importance：每条光线的额外精细采样数（分层采样）。默认0
- perturb：设置为0表示没有抖动，设置为1表示有抖动。抖动可以增加采样点的随机性。默认1
- use_viewdirs：是否使用完整的5D输入，而不是3D。5D输入包括3D位置和2D视角
- i_embed：设置为0表示使用默认的位置编码，设置为-1表示不使用位置编码。默认0
- multires：位置编码的最大频率的对数（用于3D位置）。默认10
- multires_views：位置编码的最大频率的对数（用于2D方向）。默认4
  
  我们设置 $d = 10$ 用于位置坐标 $ϕ(\bf x)$ ，所以输入是60维的向量； $d = 4$ 用于相机位姿 $ϕ(\bf d)$ 对应的则是24维
- raw_noise_std：添加到 sigma_a 输出的噪声的标准偏差，用于正则化 sigma_a 输出。默认0
- render_only：如果设置，那么不进行优化，只加载权重并渲染出 render_poses 路径
- render_test：如果设置，那么渲染测试集，而不是 render_poses 路径
- render_factor：降采样因子，用于加速渲染。设置为4或8可以快速预览。默认0
LLFF（Light Field Photography）数据集：
- factor：LLFF图像的降采样因子。默认值为8。这个值决定了在处理LLFF图像时，应该降低多少分辨率
- no_ndc：是否不使用归一化设备坐标（NDC）。如果在命令行中指定了这个参数，那么其值为True。这个选项应该在处理非前向场景时设置
- lindisp：是否在视差中线性采样，而不是在深度中采样。如果在命令行中指定了这个参数，那么其值为True
- spherify：是否处理球形360度场景。如果在命令行中指定了这个参数，那么其值为True
- llffhold：每N张图像中取一张作为LLFF测试集。默认值为8。这个值决定了在处理LLFF数据集时，应该把多少图像作为测试集
```
# 加载数据时，每隔args.llffhold个图像取一张图形
i_test = np.arange(images.shape[0])[::args.llffhold]
```

2 大致过程

2.1 加载LLFF数据

load_llff_data 函数返回五个值：images（图像），poses（姿态），bds（深度范围），render_poses（渲染姿态）和i_test（测试图像索引）
- hwf是从poses中提取的图像的高度、宽度和焦距
```
images, poses, bds, render_poses, i_test = load_llff_data(.....)
hwf = poses[0,:3,-1]
poses = poses[:,:3,:4]
```

将图像数据集划分为三个部分：训练集（i_train）、验证集（i_val）和测试集（i_test）

# 每隔args.llffhold个图像取一张做测试集
i_test = np.arange(images.shape[0])[::args.llffhold]
# 验证集 = 测试集
i_val = i_test
# 所有不在测试集和验证集中的图像
i_train = np.array([i for i in np.arange(int(images.shape[0])) if(i not in i_test and i not in i_val)])

2.2 创建神经网络模型

将采样点坐标和观察坐标通过位置编码 get_embedder 成63维和27维
实例化NeRF模型和NeRF精细模型
创建网络查询函数 network_query_fn() ，用于运行网络
创建 Adam 优化器
加载检查点（如果有），即从检查点中重新加载模型和优化器状态
创建用于训练和测试的渲染参数 render_kwargs_train、render_kwargs_test
根据数据集类型（只有LLFF才行）和参数确定是否使用NDC

2.3 准备光线

使用批处理：

对于每一个姿态，使用get_rays_np函数获取光线原点和方向（ ro+rd ），然后将所有的光线堆叠起来，得到rays
将射线的原点和方向与图像的颜色通道连接起来（ ro+rd+rgb ）
对张量进行重新排列和整形，只保留训练集中的图像
对训练数据进行随机重排

2.4 训练迭代

设置训练迭代次数 N_iters = 200000 + 1
开始进行训练迭代
- 准备光线数据：在每次迭代中，从rays_rgb中取出一批（批处理）光线数据，数量为参数值N_rand，并准备好目标值 target_s
  
  如果完成一个了周期（i_batch >= rays_rgb.shape[0] ），则对数据进行打乱
- 渲染：使用渲染函数 render()
- 计算损失：计算渲染结果的损失。这里使用了均方误差损失函数 img2mse() 来计算图像损失
  $\mathcal{L} = \sum_{\mathbf{r} \in \mathcal{R}} \left\| \hat{C}^c(\mathbf{r}) - C(\mathbf{r}) \right\|_2^2 + \left\| \hat{C}^f(\mathbf{r}) - C(\mathbf{r}) \right\|_2^2$
```
img2mse = lambda x, y : torch.mean((x - y) ** 2)
```
- 反向传播：进行反向传播，并执行优化
- 更新学习率：这里采用指数衰减的学习率调度策略，学习率在每个一定的步骤（decay_steps）内以一定的速率（decay_rate）衰减
根据参数设置的频率输出相关状态、视频和测试集

3 神经网络模型

模型结构如下：

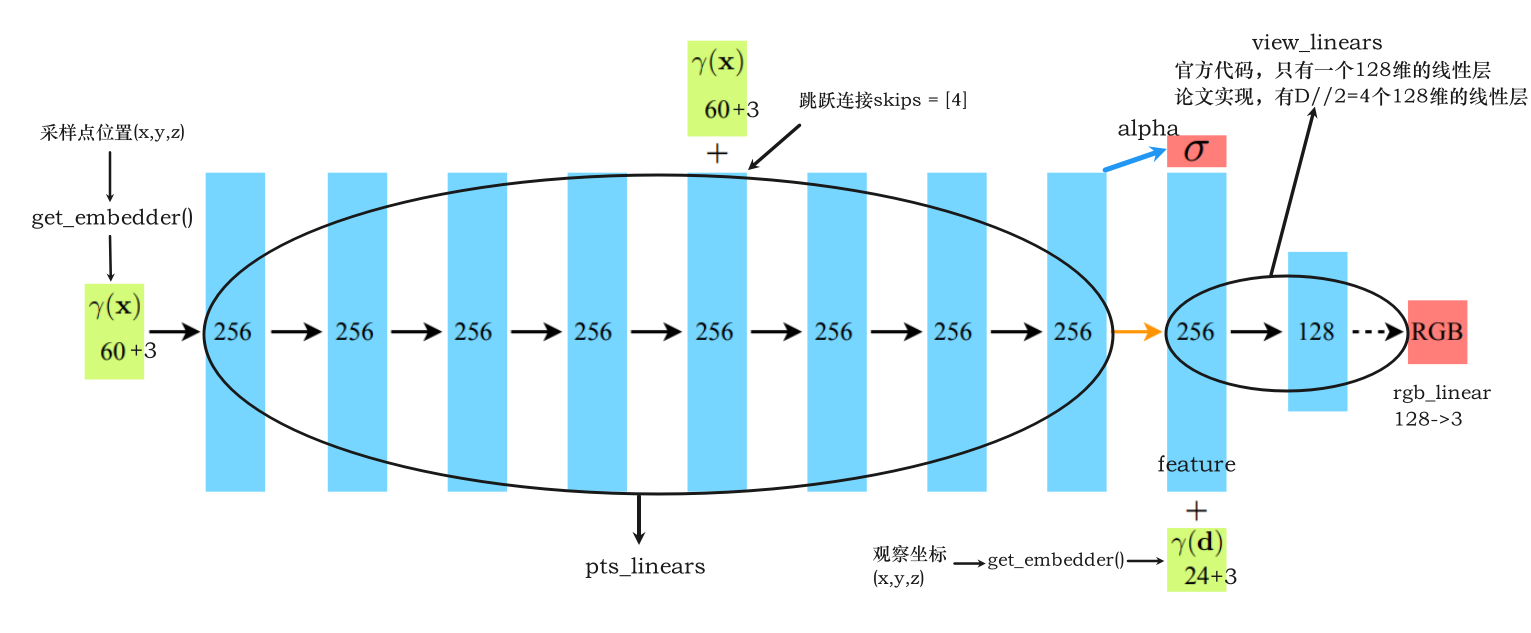
应用 ReLU 激活函数
采样点坐标和观察坐标通过位置编码成63维和27维
中间有一个跳跃连接在第四次 256->256 的线性层

跳跃连接可以将某一层的输入直接传递到后面的层，从而避免梯度消失和表示瓶颈，提高网络的性能

4 体积渲染

4.1 render()

渲染主函数是调用 render() 函数：

def render(H, W, K, chunk=1024*32, rays=None, c2w=None, ndc=True,near=0., far=1.,use_viewdirs=False, c2w_staticcam=None,**kwargs):

其有两种用法：

测试用：
```
rgb, disp, acc, _ = render(H, W, K, chunk=chunk, c2w=c2w[:3,:4], **render_kwargs)
```
c2w=c2w[:3,:4] 意味着光线的起点和方向是由函数内部通过相机参数计算得出的

这个只在 render_path() 函数中用到，其在给定相机路径下渲染图像
- 不训练只渲染时直接渲染时
- 定期输出结果时
训练用：
```
rgb, disp, acc, extras = render(H, W, K, chunk=args.chunk, rays=batch_rays,verbose=i < 10, retraw=True,**render_kwargs_train)
```
rays=batch_rays 意味着光线的起点和方向是预先计算好的，而不是由函数内部通过相机参数计算得出

这个只在训练迭代时用到：Core optimization loop 中，对从rays_rgb中取出一批（批处理）光线进行渲染，得到的 rgb 值与 target_s （也来自预先计算好的 rays_rgb ）计算 loss，来进行神经网络的训练

4.2 batchify_rays()

在主函数 render() 中，渲染工作是调用的 batchify_rays()：

主要目的是将大量的光线分批处理，以避免在渲染过程中出现内存溢出（OOM）的问题

4.3 render_rays()

分批处理函数 batchify_rays() 中的渲染操作是由 render_rays() 进行，其是真正的渲染操作的函数

def render_rays(ray_batch,network_fn,network_query_fn,N_samples,retraw=False,lindisp=False,perturb=0.,N_importance=0,network_fine=None,white_bkgd=False,raw_noise_std=0.,verbose=False,pytest=False):

其参数：光线批次（ray_batch）、网络函数（network_fn）、网络查询函数（network_query_fn）、样本数量（N_samples）等等

返回：一个字典，包含了 RGB 颜色映射、视差映射、累积不透明度等信息

其大致过程为：

从光线批次中提取出光线的起点、方向、视线方向以及近远边界
- 根据是否进行线性分布采样，计算出每个光线上的采样点的深度值
- 若设置扰动（ perturb ），则在每个采样间隔内进行分层随机采样

函数计算出每个采样点在空间中的位置

pts = rays_o[...,None,:] + rays_d[...,None,:] * z_vals[...,:,None] # [N_rays, N_samples, 3]

然后使用 network_query_fn() 对每个采样点进行预测，得到原始的预测结果 raw
使用 raw2outputs()（请看下一节4.4）函数将原始预测结果转换为 RGB 颜色映射、视差映射、累积不透明度等输出
若分层采样 N_importance > 0，调用 sample_pdf() 分层采样，并将这些额外的采样点传递给精细网络 network_fine 进行预测
最后，函数返回一个字典，包含了所有的输出结果

4.4 raw2outputs()

其将模型的原始预测转换为语义上有意义的值，主要基于论文中离散形式的积分方程实现：

累积不透明度函数 $\hat{C}(r)$ 的估计公式如下：

$\hat{C}(r) = \sum_{i=1}^{N} T_i (1 - \exp(-\sigma_i \delta_i)) c_i$

其中，

$N$ 是样本点的数量，
$T_i = \exp \left( - \sum_{j=1}^{i-1} \sigma_j \delta_j \right)$ 是权重系数
$\delta_i = t_{i+1} - t_i$ 表示相邻样本之间的距离
$c_i$ 是颜色值
$\sigma_i$ 是不透明度值（体积密度）

根据代码，我们可以得出以下关系：

$c_i$ 对应着 rgb = torch.sigmoid(raw[...,:3])，表示颜色值
$\sigma_i$ 对应着 raw[...,3]，表示不透明度值

然后，我们可以根据公式中的每个项逐一解释如何在代码中实现：

$\delta_i = t_{i+1} - t_i$ ：计算相邻样本之间的距离。在代码中：
```
 dists = z_vals[...,1:] - z_vals[...,:-1]
```
$\exp(-\sigma_i \delta_i)$ ：计算每个样本的不透明度。在代码中：
```
raw2alpha = lambda raw, dists, act_fn=F.relu: 1.-torch.exp(-act_fn(raw)*dists)alpha = raw2alpha(raw[...,3] + noise, dists)
```
$T_i = \exp \left( - \sum_{j=1}^{i-1} \sigma_j \delta_j \right)$ ：计算权重系数。在代码中：

即对 $\exp(-\sigma_i \delta_i))$ 累乘
```
torch.cumprod(torch.cat([torch.ones((alpha.shape[0], 1)), 1.-alpha + 1e-10], -1), -1)[:, :-1]
```
$\hat{C}(r) = \sum_{i=1}^{N} T_i (1 - \exp(-\sigma_i \delta_i)) c_i$ ：计算累积不透明度。在代码中：

$w_i = T_i(1 - \exp(-\sigma_i\delta_i))$
```
weights = alpha * torch.cumprod(torch.cat([torch.ones((alpha.shape[0], 1)), 1.-alpha + 1e-10], -1), -1)[:, :-1]
rgb_map = torch.sum(weights[...,None] * rgb, -2)  # [N_rays, 3]
```