SCI一区 | Matlab实现WOA-TCN-BiGRU-Attention鲸鱼算法优化时间卷积双向门控循环单元融合注意力机制多变量时间序列预测
目录
- SCI一区 | Matlab实现WOA-TCN-BiGRU-Attention鲸鱼算法优化时间卷积双向门控循环单元融合注意力机制多变量时间序列预测
- 预测效果
- 基本介绍
- 模型描述
- 程序设计
- 参考资料
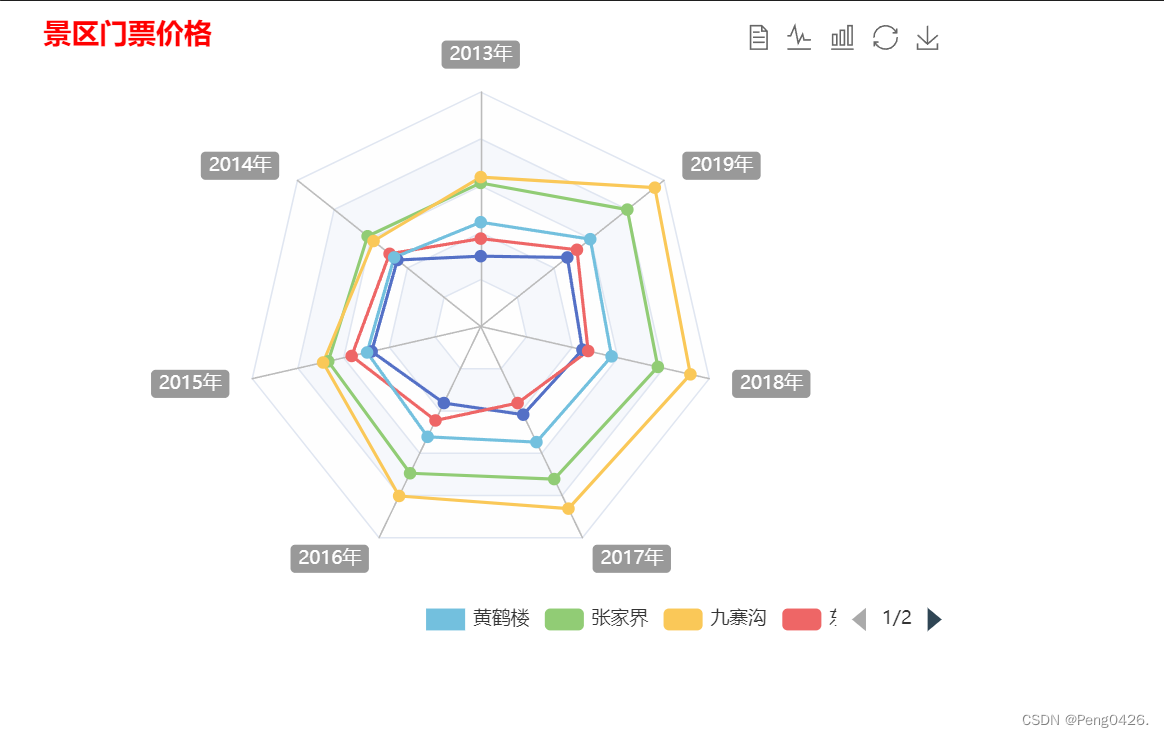
预测效果







基本介绍
1.Matlab实现WOA-TCN-BiGRU-Attention鲸鱼算法优化时间卷积双向门控循环单元融合注意力机制多变量时间序列预测,要求Matlab2023版以上,自注意力机制,一键单头注意力机制替换成多头注意力机制;
2.输入多个特征,输出单个变量,考虑历史特征的影响,多变量时间序列预测;
3.data为数据集,main.m为主程序,运行即可,所有文件放在一个文件夹;
4.命令窗口输出R2、MSE、MAE、MAPE和RMSE多指标评价;
5.优化学习率,神经元个数,注意力机制的键值, 正则化参数。
模型描述
多变量时间序列预测是一项重要的任务,它涉及对具有多个变量的时间序列数据进行预测。为了改进这一任务的预测性能,研究者们提出了许多不同的模型和算法。其中一种结合了时间卷积网络(Temporal Convolutional Network,TCN)、双向门控循环单元(Bidirectional Gated Recurrent Unit,BiGRU)和注意力机制(Attention)的模型被称为WOA-TCN-BiGRU-Attention鲸鱼算法。
该算法的核心思想是利用时间卷积网络来捕捉时间序列数据中的长期依赖关系,通过双向门控循环单元来建模序列数据的上下文信息,并通过注意力机制来自适应地加权不同变量的重要性。
具体而言,WOA-TCN-BiGRU-Attention鲸鱼算法的步骤如下:
时间卷积网络(TCN):使用一维卷积层来提取时间序列数据中的局部和全局特征。时间卷积能够通过不同大小的卷积核捕捉不同长度的时间依赖关系,从而更好地建模序列中的长期依赖。
双向门控循环单元(BiGRU):将TCN的输出作为输入,使用双向门控循环单元来编码序列数据的上下文信息。双向GRU能够同时考虑序列数据的过去和未来信息,提高了对序列中重要特征的捕捉能力。
注意力机制(Attention):通过引入注意力机制,模型可以自适应地关注输入序列中不同变量的重要性。注意力机制可以根据序列数据的不同特征,动态地调整它们在预测任务中的权重,从而提高模型的表达能力和预测准确性。
输出层:最后,根据模型的具体任务需求,可以使用不同的输出层结构,如全连接层来进行最终的预测。
通过将时间卷积网络、双向门控循环单元和注意力机制相结合,WOA-TCN-BiGRU-Attention鲸鱼算法能够更好地建模多变量时间序列数据的复杂关系,并提高预测性能。然而,需要注意的是,该算法的具体实现可能会根据具体问题和数据集的特点进行适当的调整和优化。
程序设计
- 完整源码和数据获取方式私信博主回复Matlab实现WOA-TCN-BiGRU-Attention鲸鱼算法优化时间卷积双向门控循环单元融合注意力机制多变量时间序列预测。
%% %% 鲸鱼算法优化TCN-BiGRU-Attention,实现多变量输入单步预测
clc;
clear
close allX = xlsread('data.xlsx');
num_samples = length(X); % 样本个数
kim = 6; % 延时步长(kim个历史数据作为自变量)
zim = 1; % 跨zim个时间点进行预测
or_dim = size(X,2);% 重构数据集
for i = 1: num_samples - kim - zim + 1res(i, :) = [reshape(X(i: i + kim - 1,:), 1, kim*or_dim), X(i + kim + zim - 1,:)];
end% 训练集和测试集划分
outdim = 1; % 最后一列为输出
num_size = 0.9; % 训练集占数据集比例
num_train_s = round(num_size * num_samples); % 训练集样本个数
f_ = size(res, 2) - outdim; % 输入特征维度P_train = res(1: num_train_s, 1: f_)';
T_train = res(1: num_train_s, f_ + 1: end)';
M = size(P_train, 2);P_test = res(num_train_s + 1: end, 1: f_)';
T_test = res(num_train_s + 1: end, f_ + 1: end)';
N = size(P_test, 2);% 数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);% 格式转换
for i = 1 : M vp_train{i, 1} = p_train(:, i);vt_train{i, 1} = t_train(:, i);
endfor i = 1 : N vp_test{i, 1} = p_test(:, i);vt_test{i, 1} = t_test(:, i);
end%% 优化算法优化前,构建优化前的TCN_BiGRU_Attention模型outputSize = 1; %数据输出y的维度
numFilters = 64;
filterSize = 5;
dropoutFactor = 0.1;
numBlocks = 2;layer = sequenceInputLayer(f_,Normalization="rescale-symmetric",Name="input");
lgraph = layerGraph(layer); convolution1dLayer(filterSize,numFilters,DilationFactor=dilationFactor,Padding="causal")layerNormalizationLayerreluLayerdropoutLayer(dropoutFactor) additionLayer(2,Name="add_"+i)];% Add and connect layers.lgraph = addLayers(lgraph,layers);lgraph = connectLayers(lgraph,outputName,"conv1_"+i);% Skip connection.if i == 1% Include convolution in first skip connection.layer = convolution1dLayer(1,numFilters,Name="convSkip");lgraph = addLayers(lgraph,layer);lgraph = connectLayers(lgraph,outputName,"convSkip");lgraph = connectLayers(lgraph,"convSkip","add_" + i + "/in2");elselgraph = connectLayers(lgraph,outputName,"add_" + i + "/in2");end% Update layer output name.outputName = "add_" + i;
endtempLayers = flattenLayer("Name","flatten");
lgraph = addLayers(lgraph,tempLayers);tempLayers = gruLayer(NumNeurons,"Name","gru1");
lgraph = addLayers(lgraph,tempLayers);tempLayers = [FlipLayer("flip3")gruLayer(NumNeurons,"Name","gru2")];
lgraph = addLayers(lgraph,tempLayers);tempLayers = [concatenationLayer(1,2,"Name","concat")参考资料
[1] https://blog.csdn.net/kjm13182345320/article/details/128577926?spm=1001.2014.3001.5501
[2] https://blog.csdn.net/kjm13182345320/article/details/128573597?spm=1001.2014.3001.5501