数据结构/C++：哈希表-编程知识

数据结构/C++：哈希表

- 哈希表概念
- 哈希函数
- - 直接定址法
  - 除留余数法
- 哈希冲突
- - 闭散列 - 开放定址法
  - - 基本结构
    - 查找
    - 插入
    - 删除
    - 总代码展示
  - 开散列 - 哈希桶
  - - 基本结构
    - 查找
    - 插入
    - 删除
    - 代码展示

哈希表概念

在顺序表中，查找一个数据的时间复杂度为O(N)；在平衡树这种树形结构中，查找一个数据的时间复杂度为O( $log_{}{N}$ )。尽管平衡树的搜索已经很优秀了，但是我们理想中的搜索方法是不经过任何比较，一次直接从数据结构中拿到想要的元素，也就是把搜索的复杂度优化为O(1)。这看似天方夜谭，但是哈希表可以做到，本博客就讲解哈希表，以及它的多种实现方案。

如果某个字符串中只有小写字母a-z，请你统计所有字母出现的次数。你会怎么做？

我们可以创建一个长为26的数组arr，然后让a对应arr[0]，b对应arr[1]以此类推，每个位置都对应一个字母，然后遍历一遍字符串。假设当前字母为i，按照转换规则：arr[i - 'a']++进行转换。

其实这就是一个哈希表的思想，我们把数据a - z通过i - 'a'这个映射关系转化为了一个数字，然后再把对应的数组下标赋予对应的意义。此时这个数组就是一个哈希表。

所以哈希表可以简单理解为：把数据转化为数组的下标，然后用数组的下标对应的值来表示这个数据。如果我们想要搜索这个数据，直接计算出这个数据的下标，然后就可以直接访问数组对应的位置，所以可以用O(1)的复杂度直接找到数据。

其中，这个数据对应的数字叫做关键码(Key)，这个把关键码转化为下标的规则，叫做哈希函数(Hash)。

要注意的是，有一些数据并不是整型，比如字符串，对象等等。对于这种数据，我们要先用一套规则把它们转化为整数（关键码），然后再通过哈希函数映射为数组下标。

哈希函数

哈希函数原则：

哈希函数转换后，生成的地址（下标）必须小于哈希表的最大地址（下标）
哈希函数计算出来的地址（下标）必须均匀地分布
哈希函数尽可能简单

接下来我们看一些常见的哈希函数：

直接定址法

取关键字的某个线性函数为哈希表的地址：

$\text { Hash (Key) }=A × \text { Key }+B$

这种哈希函数特点就是简单，均匀。但是由于我们没有限制这个地址的范围，其有可能对数组越界访问，所以要提前知道数据的范围。

比如我们刚刚通过字母的ASCII码直接减去a的ASCII码的过程，就是一个直接定址过程。在这之前，我们知道小写字母只有26个，所以没有发生越界访问。

这种哈希函数在一些数据简单的算法题中高频使用。

除留余数法

假设哈希表的地址数目为m，取Key对m取模后得到的值作为下标

$\text { Hash (Key) }=\text Key\ \% \ m$

该方法通过取模，简单地把地址控制在了目标范围内，STL库中使用的就是这种方法，本博客后续也使用这种方法。

此外还有一些哈希函数，但是都不常用了，此处不做讲解了。

哈希冲突

现在我们采用除留余数法作为哈希函数，我们尝试对一个长度为10的哈希表插入值：

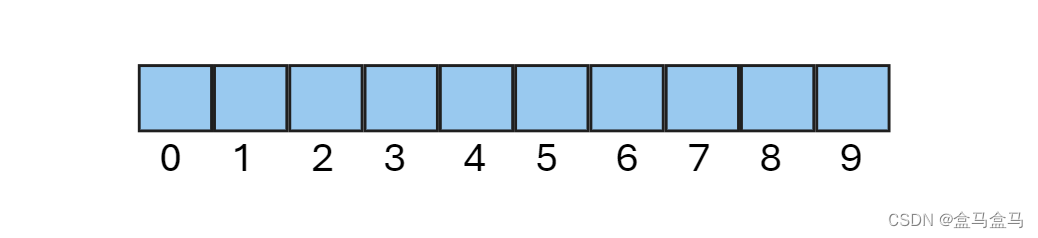
在这里插入图片描述
其哈希函数为：
$\text { Hash (Key) }=\text Key\ \% \ 10$

现在我们插入1，8，15，124四个数字：
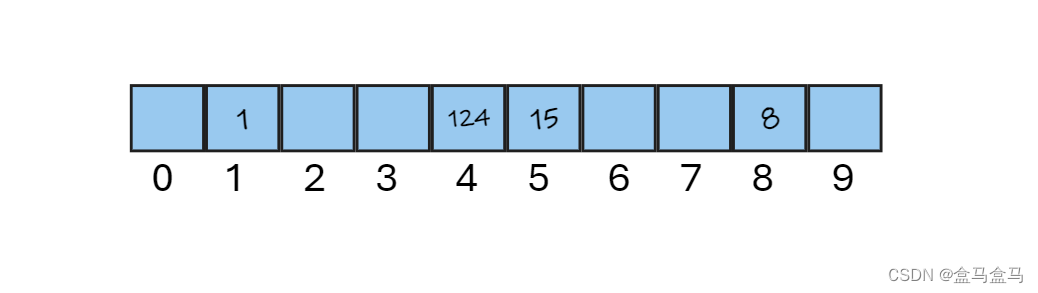
在这里插入图片描述

根据哈希函数的规则，我们把这四个数字映射到了合适的位置。现在我们载插入数字14，你会发现14 % 10 = 4，但是下标为4的位置已经被124占用了，这该怎么办？

这种多个数据占用一个位置的情况，叫做哈希冲突，解决哈希冲突有两种方法，分别是闭散列和开散列，我们现在就讲解两种方案，以及对应哈希表的实现方法。

闭散列 - 开放定址法

闭散列，也叫做开放定址法，当发生哈希冲突时，如果哈希表没有被装满，说明哈希表中还有空位置，那么我们可以把发生冲突的数据放到下一个空位置去。

比如在刚刚的情况中，我们插入14，发现下标为4的位置被占用了，于是到下标为5的位置，发现下标为5的位置也被占用了，于是到下标为6的位置。最后就插入下标6的位置：

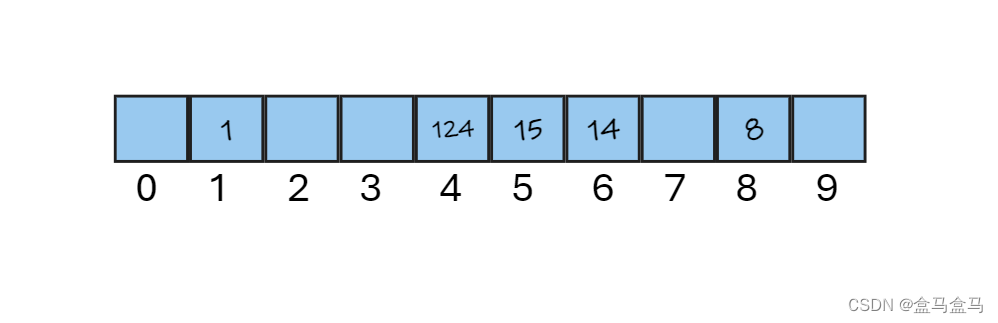
在这里插入图片描述

当我们查找14的时候，先通过哈希函数计算出下标为4，然后发现哈希表中下标为4的位置不是14，于是向后查找，发现下标为5的位置不是14，再往后查找，发现14在下标为6的位置。

再比如，我们查找44的时候，先通过哈希函数计算出下标为4，然后发现哈希表中下标为4的位置不是44，于是向后查找，发现下标为5的位置不是44，再往后查找，发现下标为6的位置不是44，再向后查找，发现下标为7的位置没有数据了，于是推断出44数据不存在于哈希表中。

基本结构

首先我们需要一个枚举，来标识哈希表的不同状态：

enum State
{EMPTY,EXIST,DELETE
};

EMPTY：空节点
EXIST：数值存在
DELETE：数值被删除

为什么要这样标识节点呢？
我们看到以下情况：
在这里插入图片描述

现在我们将15这个数据从哈希表中删除，其面临着两个问题：

删除后，应该替换为什么数据？如果我们替换后的数据与插入的数据冲突怎么办？

因此我们不能直接替换来删除一个数据，而是用一个额外的变量来标识状态：EMPTY空，EXIST存在。

现在我们删除后试试看：
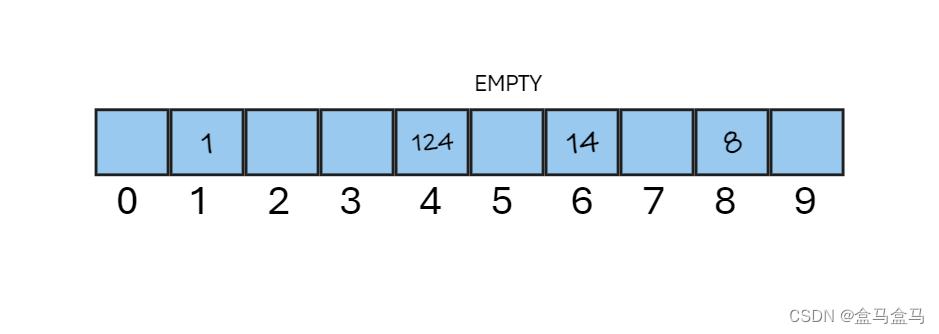
在这里插入图片描述
现在我们面临第二个问题：

我们删除节点后，会面临原本连续的数据被截断的问题。如果我们现在要查找数据14，其会从下标为4的位置开始查找，但是查找到下标为5的位置发现没有数据了，于是停止查找。

这个过程中，由于删除后的数据被标识为EMPTY，此时查找就发生了问题，因此我们要把删除DELETE和空EMPTY区分开来，当查找数据时，发现DELETE的节点应该继续往后查找。

最后我们就得到了节点的三种状态标识：
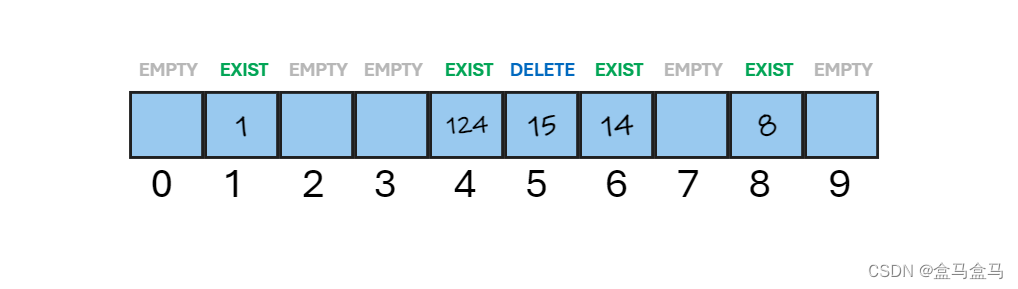
在这里插入图片描述

现在我们再看到哈希表的基本结构：

enum State
{EMPTY,EXIST,DELETE
};template<class K, class V>
struct HashData
{pair<K, V> _kv;State _state = EMPTY;//标记状态
};template<class K, class V>
class HashTable
{
public:HashTable(size_t size = 10){_tables.resize(size);}private:vector<HashData<K, V>> _tables;//哈希表size_t _n = 0;//元素个数
};

哈希表的节点HashData：

pair<K, V> _kv：哈希表存储的键值对
State _state = EMPTY：标识节点的状态，默认状态为空-EMPTY

在哈希表的类HashTable中，存在两个成员变量：

vector<HashData<K, V>> _tables：哈希表，表中存储着HashData<K, V>也就是键值对
size_t _n = 0：哈希表中的元素个数，初始值为0

HashTable构造函数：

HashTable(size_t size = 10)
{_tables.resize(size);
}

一开始给哈希表10个大小的空间，装不下再扩容。

查找

想要在哈希表中查找数据，无非就遵顼以下规则：

通过哈希函数计算出数据对应的地址
去地址处查找，如果地址处不是目标值，往后继续查找
遇到EMPTY还没有找到，说明数据不存在哈希表中
遇到DELETE和EXIST，继续往后查找

代码如下：

HashData<K, V>* Find(const K& key)
{size_t hashi = key % _tables.size();while (_tables[hashi]._state != EMPTY){if (_tables[hashi]._kv.first == key&& _tables[hashi]._state == EXIST)return &_tables[hashi];hashi++;hashi %= _tables.size();}return nullptr;
}

代码解析：

HashData<K, V>* Find(const K& key)：
查找函数，输入一个key值，返回指向该值节点的指针

size_t hashi = key % _tables.size();：
通过除留余数法，计算出key对应的下标hashi

while (_tables[hashi]._state != EMPTY)：
只要hashi对应的下标不为EMPTY，就继续往后查找

if (_tables[hashi]._kv.first == key&& _tables[hashi]._state == EXIST)：
只有当前节点存在EXIST，并且节点内的值等于目标值，就返回该节点的地址

hashi++;，hashi %= _tables.size();：
如果当前节点不是目标值，往后一个节点查找。但是这个过程有可能越界，此时如果遇到哈希表末尾，则通过取模计算从头部继续查找

return nullptr;：
如果前面没有找到，说明目标值不存在，返回空指针

但是当前的代码存在一个问题：哈希表作用于泛型，key % _tables.size()有可能是违法的行为，因为key可能不是一个数字。这该怎么办？

解决以上问题，就是把传进来的数据转化为整型。对此我们可以在模板中多加一个仿函数的参数，用户可以在仿函数中自定义数据 -> 整型的转换规则，然后我们在对这个整型使用除留余数法获取地址。

在那之前，我们可以先写一个仿函数，用于处理整型 -> 整型的转化：

struct HashFunc
{size_t operator()(const K& key){return (size_t)key;}
};

因为本身就是整型，所以返回自己就可以了。
另外的，由于我们经常使用哈希表存储字符串，所以我们还可以写一个string -> 整型的转换规则：

经过研究，有人发现：把字符串的每一位的ASCII加起来，并且每次加和后，乘以一个数值，得到的数值，分散性很强：

struct HashFunc
{size_t operator()(const string& s){size_t hash = 0;for (auto& e : s)//把字符串的每一个字符ASCII码值加起来{hash += e;hash *= 131; // 31, 131313(任意由1，3间断排列的数字)}return hash;}
};

其中，这个数值由1和3间断地排列，这样得出来的值分散性最强，我此处采用数值131。

在STL中，整型-> 整型转化的函数，被写为了一个模板，而这个string -> 整型被写为了一个模板特化：

template<class K>
struct HashFunc
{size_t operator()(const K& key){return (size_t)key;}
};template<>
struct HashFunc<string>
{size_t operator()(const string& s){size_t hash = 0;for (auto& e : s)//把字符串的每一个字符ASCII码值加起来{hash += e;hash *= 131; // 31, 131313(任意由1，3间断排列的数字)}return hash;}
};

现在我们给哈希表加上第三个模板参数Hash，用于传入仿函数：

template<class K, class V, class Hash>
class HashTable
{};

然后我们将这个HashFunc<K>仿函数作为哈希表的第三个模板参数的默认值：

template<class K, class V, class Hash = HashFunc<K>>
class HashTable
{};

由于我们的string -> 整型被写为了一个模板特化，此时我们的string也可以通过默认值直接转化，不用自己传入模板参数。

原先我们获得下标的代码如下：

size_t hashi = key % _tables.size();

现在我们要通过仿函数来统一获得整型，再进行除留余数操作：

Hash hs;
size_t hashi = hs(key) % _tables.size();

这样我们就可以让多种数据转为整型了。

插入

插入的基本逻辑如下：

先通过Find接口，查找目标值在不在哈希表中，如果目标值已经存在，返回flse，表示插入失败
通过哈希函数计算出目标值对应的下标
向下标中插入数据：

如果下标对应的位置已经有数据，往后查找，直到某一个位置为EMPTY或者DELETE
如果下标对应的位置没有数据，直接插入

插入后，把对应位置的状态转化为EXIST

代码如下：

bool Insert(const pair<K, V>& kv)
{if (Find(kv.first))return false;Hash hs;//仿函数实例化出的对象size_t hashi = hs(kv.first) % _tables.size();//获得目标值对应的下标while (_tables[hashi]._state == EXIST)//往后查找合适的位置插入{hashi++;hashi %= _tables.size();}_tables[hashi]._kv = kv;//插入_tables[hashi]._state = EXIST;//改变状态_n++;//哈希表中的元素个数+1return true;
}

目前还有一个问题，那就是：如果哈希表满了怎么办？

如果哈希表满了，我们就要进行扩容操作，但是我们并不是在哈希表满的时候扩容。其实我们可以发现，当这个哈希表越满，我们查找数据的效率就越低，甚至说：如果查找一个不存在的数据，我们可能要用O(N)的复杂度遍历整个哈希表。因此我们因该把哈希表的负载率控制在一定值，当超过一定值，我们就要进行扩容操作。在此我把负载率控制在70%，负载率超过70%，我们就进行扩容：

if ((double)_n / _tables.size() >= 0.7)
{//扩容
}

要注意的是，_n和_tables.size()都是整型，它们之间进行除法是整数除法，所以我们要把前者强制转化为double，让其进行小数除法。

对于扩容，我有两个方案：

新建一个更大的vector，把所有数值重新映射到哈希表中
新建一个更大的哈希表，把所有数值insert到哈希表中，然后把新的哈希表里面的vector交换给自己

两者对比，有一个重要的区别就是：我们已经写过哈希表的insert函数了，我们只要遍历一遍原哈希表的数据，就可以完成插入操作。但是对于vector，我们想要重新映射，就需要重写一个vector的映射逻辑。因此最好采用后者：

if ((double)_n / _tables.size() >= 0.7)
{size_t newSize = _tables.size() * 2;HashTable<K, V, Hash> newHT(newSize);for (auto& e : _tables){if (e._state == EXIST)newHT.Insert(e._kv);}_tables.swap(newHT._tables);
}

代码解析：

size_t newSize = _tables.size() * 2:
计算出新的哈希表的大小，这里采用二倍扩容

HashTable<K, V, Hash> newHT(newSize)：
创建一个新的哈希表newHT，其大小为原哈希表的两倍

for (auto& e : _tables)：
遍历原哈希表（其实就是遍历哈希表里面的数组）

if (e._state == EXIST) {newHT.Insert(e._kv)}：
只要当前节点的值状态为EXIST，就把它插入到新表

_tables.swap(newHT._tables);：
把新创建的哈希表的vector交换给当前哈希表。

这里有一个细节问题，那就是我们临时创建的哈希表newHT生命周期仅在这个if的括号内。当出了生命周期，newHT就会调用析构函数，自动销毁内部的vector，而我们把原先的较小的那个vector交换给了这个newHT，此时这个newHT还起到了销毁原先的小vector的功能。

插入总代码：

bool Insert(const pair<K, V>& kv)
{if (Find(kv.first))return false;if ((double)_n / _tables.size() >= 0.7){size_t newSize = _tables.size() * 2;HashTable<K, V, Hash> newHT(newSize);for (auto& e : _tables){if (e._state == EXIST)newHT.Insert(e._kv);}_tables.swap(newHT._tables);}Hash hs;size_t hashi = hs(kv.first) % _tables.size();while (_tables[hashi]._state == EXIST){hashi++;hashi %= _tables.size();}_tables[hashi]._kv = kv;_tables[hashi]._state = EXIST;_n++;return true;
}

删除

删除也是一个比较简单的逻辑：

先通过Find接口找到要删除的值

如果没找到，返回false，表示删除失败
如果找到，把对应节点的状态改为DELETE

最后再把哈希表的_n - 1，表示存在的节点数少了一个。

代码如下：

bool Erase(const K& key)
{HashData<K, V>* ret = Find(key);if (ret){ret->_state = DELETE;_n--;return true;}return false;
}

至此我们就完成了一个闭散列的哈希表。

总代码展示

template<class K>
struct HashFunc
{size_t operator()(const K& key){return (size_t)key;}
};template<>
struct HashFunc<string>
{size_t operator()(const string& s){size_t hash = 0;for (auto& e : s)//把字符串的每一个字符ASCII码值加起来{hash += e;hash *= 131; // 31, 131313(任意由1，3间断排列的数字)}return hash;}
};enum State
{EMPTY,EXIST,DELETE
};template<class K, class V>
struct HashData
{pair<K, V> _kv;State _state = EMPTY;//标记状态
};template<class K, class V, class Hash = HashFunc<K>>
class HashTable
{
public:HashTable(size_t size = 10){_tables.resize(size);}HashData<K, V>* Find(const K& key){Hash hs;size_t hashi = hs(key) % _tables.size();while (_tables[hashi]._state != EMPTY){if (_tables[hashi]._kv.first == key&& _tables[hashi]._state == EXIST)return &_tables[hashi];hashi++;hashi %= _tables.size();}return nullptr;}bool Insert(const pair<K, V>& kv){if (Find(kv.first))return false;if ((double)_n / _tables.size() >= 0.7){size_t newSize = _tables.size() * 2;HashTable<K, V, Hash> newHT(newSize);for (auto& e : _tables){if (e._state == EXIST)newHT.Insert(e._kv);}_tables.swap(newHT._tables);}Hash hs;size_t hashi = hs(kv.first) % _tables.size();while (_tables[hashi]._state == EXIST){hashi++;hashi %= _tables.size();}_tables[hashi]._kv = kv;_tables[hashi]._state = EXIST;_n++;return true;}bool Erase(const K& key){HashData<K, V>* ret = Find(key);if (ret){ret->_state = DELETE;_n--;return true;}return false;}private:vector<HashData<K, V>> _tables;size_t _n = 0;//元素个数
};

开散列 - 哈希桶

其实闭散列并不是一个优秀的方案来处理哈希冲突，因为一个数值的位置被占用后，这个数值就会去占用别人的位置，这种拆东墙补西墙的行为，会导致恶性循环，查找的效率也很低。最差的情况实际复杂度会退化到O(N)。

在STL库中，采用的是更加优秀的开散列方案。

哈希表的数组vector中，不再直接存储数据，而是存储一个链表的指针。当一个数值映射到对应的下标后，就插入到这个链表中。其中每一个链表称为一个哈希桶，每个哈希桶中，存放着哈希冲突的元素。

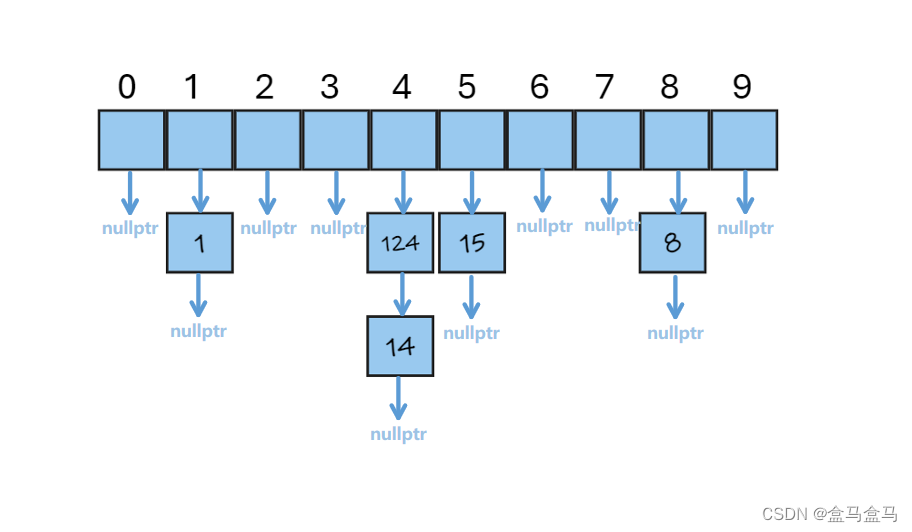
在这里插入图片描述

一般而言，我们的链表使用单向链表就够了，因为一个哈希桶中一般不会出现太多元素。

现在我们来尝试实现这个开散列哈希表：

基本结构

对于每一个节点，其要存储当前节点的值，也要存储下一个节点的指针，基本结构如下：

template<class K, class V>
struct HashNode
{HashNode<K, V>* _next;pair<K, V> _kv;HashNode(const pair<K, V>& kv):_kv(kv),_next(nullptr){}
};

_kv：节点存储但键值对
_next：指向下一个节点的指针

哈希表：

template<class K, class V, class Hash = HashFunc<K>>
class HashTable
{typedef HashNode<K, V> Node;
public:HashTable(size_t size = 10){_tables.resize(size);}private:vector<Node*> _tables; //链表指针数组size_t _n = 0;//元素个数
};

基本结构和开散列是一致的，但是vector内部存储的不再是节点了，而是指向节点的指针Node*。

对于这个哈希表，由于我们开辟了外部资源，所以我们还要自己写一个析构函数，防止内存泄漏：

~HashTable()
{for (size_t i = 0; i < _tables.size(); i++){Node* cur = _tables[i];while (cur){Node* next = cur->_next;delete cur;cur = next;}_tables[i] = nullptr;}
}

基本逻辑就是遍历整个vector，然后把每个元素指向的链表都delete释放掉。

查找

查找的基本逻辑如下：

先通过哈希函数计算出数据对应的下标
通过下标找到对应的链表
遍历链表，找数据

如果某个节点的数据匹配上了，返回该节点指针
如果遍历到了nullptr，返回空指针表示没找到

代码如下：

Node* Find(const K& key)
{Hash hs;size_t hashi = hs(key) % _tables.size();Node* cur = _tables[hashi];while (cur){if (cur->_kv.first == key)return cur;cur = cur->_next;}return nullptr;
}

这个很基础，就不详细解释了。

插入

插入的基本逻辑如下：

先通过Find接口，查找目标值在不在哈希表中，如果目标值已经存在，返回flse，表示插入失败
通过哈希函数计算出目标值对应的下标
向下标中插入数据

我们思考一个问题：我们将数据插入到链表中时，是头插还是尾插？
由于我们不知道访问同一个哈希桶中的数据时，会访问哪一个，所以哈希桶中数据的先后是没有区别的。但是尾插需要找尾，会增加插入的时间，因此我们直接头插就可以了。

代码如下：

bool Insert(const pair<K, V>& kv)
{if (Find(kv.first))return false;Hash hs;size_t hashi = hs(kv.first) % _tables.size();//计算下标Node* newNode = new Node(kv);//创建节点newNode->_next = _tables[hashi];//头插_tables[hashi] = newNode;++_n;//更新元素个数return true;
}

经过以上逻辑，我们就可以插入一个数据到哈希表中了。但是我们面临着相同的问题，如果哈希表太满，时间复杂度会发生退化，因此我们要在负载率过高时进行扩容。

与闭散列不同的是，开散列的哈希桶之间不会互相影响，因此这个负载率可以高一些。在STL中，其负载率控制在100%。

if (_n == _tables.size())//负载率100%
{//扩容
}

我们可以像之前一个，创建一个新的哈希表，然后把所有的值都插入进去，这当然是一个不错的办法。但是闭散列与开散列有一个很大的区别就是，哈希桶会额外创建大量的链表节点。如果我们单纯的进行插入，就要把原先的所有节点释放掉，再创建新的节点。这样会浪费很多时间。我们最好把原先创建的节点利用起来，因此我们要重写一个逻辑，把原先的节点进行迁移。

先创建一个新的vector：

vector<Node*> newTables(_tables.size() * 2, nullptr);

新的vector的大小是原先的两倍，所有节点初始化为nullptr；

再用两层循环遍历所有节点：


for (size_t i = 0; i < _tables.size(); i++)
{Node* cur = _tables[i];while (cur){Node* next = cur->_next;cur = next;}
}

对于每一个节点，我们要得到它的值，然后计算出它在新的表中的下标，插入到对应的下标位置：

size_t hashi = hs(cur->_kv.first) % newTables.size();//计算下标cur->_next = newTables[hashi];//头插
newTables[hashi] = cur;//头插

要注意的是，我们每遍历完一个哈希桶，要把原先的vector中指向哈希桶的指针置空，否则原先的vector在销毁的时候，调用析构函数，会把我们转移的节点给销毁掉。

扩容总代码如下：

if (_n == _tables.size())
{vector<Node*> newTables(_tables.size() * 2, nullptr);for (size_t i = 0; i < _tables.size(); i++){Node* cur = _tables[i];while (cur){Node* next = cur->_next;size_t hashi = hs(cur->_kv.first) % newTables.size();cur->_next = newTables[hashi];newTables[hashi] = cur;cur = next;}_tables[i] = nullptr; //防止移交的节点被析构}_tables.swap(newTables);
}

删除

删除逻辑：

通过哈希函数计算出对应的下标
到对应的哈希桶中查找目标值

如果找到，删除对应的节点
如果没找到，返回false表示删除失败

_n - 1表示删除了一个元素

代码如下：

bool Erase(const K& key)
{Hash hs;size_t hashi = hs(key) % _tables.size();Node* prev = nullptr;Node* cur = _tables[hashi];while (cur){if (cur->_kv.first == key){if (prev)prev->_next = cur->_next;else_tables[hashi] = cur->_next;delete cur;--_n;return true;}prev = cur;cur = cur->_next;}return false;
}

这个逻辑也比较简单，但是要注意的是，我们删除链表节点后，要把这个节点的前后连接起来，所以我们需要一个额外的parent来标识前面一个节点。

代码展示

template<class K>
struct HashFunc
{size_t operator()(const K& key){return (size_t)key;}
};template<>
struct HashFunc<string>
{size_t operator()(const string& s){size_t hash = 0;for (auto& e : s)//把字符串的每一个字符ASCII码值加起来{hash += e;hash *= 131; // 31, 131313(任意由1，3间断排列的数字)}return hash;}
};template<class K, class V>
struct HashNode
{HashNode<K, V>* _next;pair<K, V> _kv;HashNode(const pair<K, V>& kv):_kv(kv),_next(nullptr){}
};template<class K, class V, class Hash = HashFunc<K>>
class HashTable
{typedef HashNode<K, V> Node;
public:HashTable(size_t size = 10){_tables.resize(size);}~HashTable(){for (size_t i = 0; i < _tables.size(); i++){Node* cur = _tables[i];while (cur){Node* next = cur->_next;delete cur;cur = next;}_tables[i] = nullptr;}}Node* Find(const K& key){Hash hs;size_t hashi = hs(key) % _tables.size();Node* cur = _tables[hashi];while (cur){if (cur->_kv.first == key)return cur;cur = cur->_next;}return nullptr;}bool Insert(const pair<K, V>& kv){if (Find(kv.first))return false;Hash hs;//哈希桶情况下，负载因子到1才扩容if (_n == _tables.size()){vector<Node*> newTables(_tables.size() * 2, nullptr);for (size_t i = 0; i < _tables.size(); i++){Node* cur = _tables[i];while (cur){Node* next = cur->_next;size_t hashi = hs(cur->_kv.first) % newTables.size();cur->_next = newTables[hashi];newTables[hashi] = cur;cur = next;}_tables[i] = nullptr; //防止移交的节点被析构}_tables.swap(newTables);}size_t hashi = hs(kv.first) % _tables.size();Node* newNode = new Node(kv);newNode->_next = _tables[hashi];_tables[hashi] = newNode;++_n;return true;}bool Erase(const K& key){Hash hs;size_t hashi = hs(key) % _tables.size();Node* prev = nullptr;Node* cur = _tables[hashi];while (cur){if (cur->_kv.first == key){if (prev)prev->_next = cur->_next;else_tables[hashi] = cur->_next;delete cur;--_n;return true;}prev = cur;cur = cur->_next;}return false;}private:vector<Node*> _tables; //链表指针数组size_t _n = 0;//元素个数
};