题目描述：

  给定一个数n，再给出n个数，现在要求你求出这些数的乘积的约数个数总和，结果对1e9+7取模。

取值范围：1<n<100; 1<ni<2e9;

分析步骤：

  第一：要求约数的个数，我们有许多的求法，比如试除法，线性筛法求。那么本文就将两种方法都讲一遍。题目中说要求出给出的数的乘积的约数个数，如果我们真的去求出了数的乘积总和，那么一定会溢出int函数因为 ni 最大值为2e9只要稍微再乘个数都会超过，所以我们仔细想想，其实我们只需要把每一个数都拆成约数，把他们的约数是哪些分别都统计一下，再结合公式就可以得到最终的答案

第二：试除法求出约数个数。

1. 输入一个n，再用while循环不断地将数输入进去，定义有一个哈希表first代表着具体的约数是哪个；second代表着这个约数有多少。

2. 用for循环不断地去寻找，如果 i 是x的约数的话那么就将mp[i]++那么约束大小为i的个数就++，再将 x 除去i ，直到 i 不再是x的约数的话，while循环结束。在判断一下最终剩下来的数是不是 1 ， 如果不是1的话那么这个数就也是一个约数我们将其存储起来。

3. 定义res为1，运用迭代器向后遍历，利用公式将每一个约数的个数+1的和相乘得到的就是最终的答案。

#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;
typedef long long LL;
const int N = 1e6+10 , MOD = 1e6+1;unordered_map<int, int >mp;int main()
{int n ; cin>>n;while(n --){int x ; cin>>x;for(int i = 2 ; i <= x / i ; i++){while(x % i == 0){mp[i]++;x/=i;}}if(x > 1) mp[x]++;}LL res = 1;for(auto t : mp){res *= (1+t.second) % MOD;}cout<<res;return 0;
}

 但是我们知道其实试除法求出约数个数时间复杂度为根号n，那么当求1~n的所有约数的个数的时候时间复杂度为n根号n那么只要数据量稍微大一点就会超时，所以接下来我们介绍欧拉筛也就是线性筛法将时间复杂度优化为n。 

  第三：线性筛法求出1~n的约数个数

1. 既然是线性筛法我们就要套用线性筛的模板，

2. 首先明确一下我们的数组分别是有什么用 p[N] 收集质数, vis[N]判断此数是否遍历过 ,  a[N]记录 i 的最小质数出现的次数 ; d[N] i 数的约数个数;

3. 初始化d[1]为1，用for循环去遍历，如果这个值是没有被遍历过的那么这个值就一定是质数，我们把他收集进入我们的 p 数组，更新d[i]为2，因为由于该数是个质数那么他的约数就一定只有1 和 他们本身，所以d[i]的约数个数为2，更新a[i]为1，因为该数是质数所以他最小的质数出现的次数也一定是他本身所以是1。

4. 再用for循环让后面的值一定只被他最小的质因子给除去我们将该点定义为true表示该点不是质数，

5. 进入判断如果：i % p[j] == 0 。 由于p[j]一定是它最小的质因子所以这个式子成立的话，就代表着a[m] 比 a[i] 多了一个质因子所以加1.所以现在的d[m]和原来的比起来，就只有c1那部分有点差别，所以只要除去原来的部分，再乘上新加的部分就可以得出答案了。

6. 如果判断式子不成立的话则代表这个数是一个新的质因子，因为新的质因子的话那就只有两个约数（1和本身），只有一个质因子（本身），所以我们更新a[m]为1，更新d[m]则为2*d[i]因为我们看看公式他是要将质因子个数+1的和相乘，所以比原来多了一个质因子套入公式（1+1）== 2 所以是原来的两倍。

 

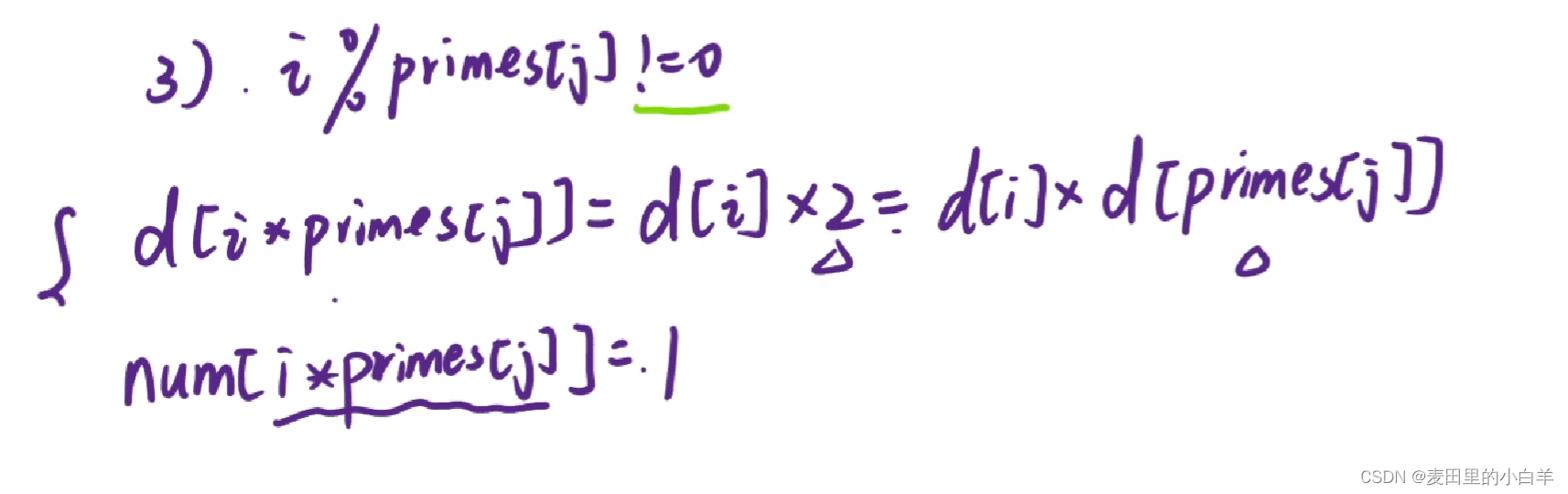
void get_d(int n){d[1] = 1;for(int i = 2 ; i <= n ; i ++){if(!vis[i]){p[cnt++] = i;d[i] = 2;a[i] = 1;}for(int j = 0; p[j] * i <= n ; j ++){int m = p[j] * i;vis[m] = true;if(i % p[j] == 0){a[m] = a[i]+1;d[m] = d[i]/a[m]*(a[m]+1);break;}else{d[m] = 2*d[i];a[m] = 1;}   }}
}

  

线性筛代码：

#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 1e6+10;int p[N] , vis[N] , cnt;
int a[N] ;
int d[N] ;void get_d(int n){d[1] = 1;for(int i = 2 ; i <= n ; i ++){if(!vis[i]){p[cnt++] = i;d[i] = 2;a[i] = 1;}for(int j = 0; p[j] * i <= n ; j ++){int m = p[j] * i;vis[m] = true;if(i % p[j] == 0){a[m] = a[i]+1;d[m] = d[i]/a[m]*(a[m]+1);break;}else{d[m] = 2*d[i];a[m] = 1;}   }}
}int main()
{int x ; cin>>x;get_d(x);cout<<d[x]<<endl;return 0;
}