分披萨
- 有大小不同的奇数块披萨;
- 从A开始轮流取披萨,第一块可以任意选取,其他都必须从缺口开始选;
- B每次都选最大块的, A知道B的想法;
- 求A能获得的披萨块总和的最大值;
输入描述:
第一行输入n(奇数,表示披萨块数), [3, 500)
接下来的n行,每行输入一个披萨块的大小
输出描述:
A能获得的披萨块总和的最大值;
示例1
输入:
5
8
2
10
5
7
输出:
19
说明:
A拿10
B拿5
A拿7
B拿8
A拿2
此时A拿到最多19
示例2:
输入:
7
4
3
8
2
10
9
20
输出:
35
示例3
输入:
23
45
78
21
12
14
52
76
123
302
34
43
73
37
89
98
101
102
201
120
24
15
17
28
输出:
1032
思路:
-
回溯法
-
A先随意取一块,有n种取法,0 1 2… n-1
-
A取的当前索引i
- left = (i + 1 + n) % n;
- right = (i -1 + n) % n;
- backtrace(left, right),先B取一个较大的,然后A取并赋值matrix[left][right],其中matrix是一个n*n的矩阵,初始化为0;
- matrix[left][right] = max(A先取左边的值 + 回溯结果,A先取右边的值+回溯结果),并返回
- left == right 时,matrix[left][right] 赋值并返回
- 针对示例1 更新后的matrix为:
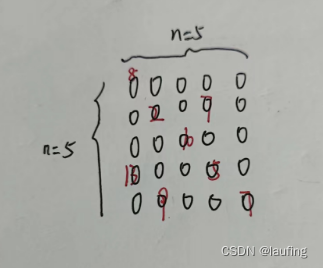
-
A取的当前索引i对应的值 + 回溯值,若大于result,则更新result;
# 输入总块数
n = int(input().strip())# 每块的大小 - 列表
nums = []
for i in range(n):nums.append(int(input().strip()))# A取的时候,矩阵对应[left, right]位置保存A可以获取的最大和
matrix = [[0 for i in range(n)] for j in range(n)]# 回溯函数
def backtrace(left, right):# 全局变量global n, nums, matrix# B取if nums[left] > nums[right]:left = (left + n + 1) % nelif nums[left] < nums[right]: # 块的大小各不相同right = (right + n - 1) % n # 右边的指针向左走一步# A 取并 给matrix赋值(matrix对应位置未赋值时)if matrix[left][right] <= 0: # 为初始值if left == right: # 结束matrix[left][right] = nums[left]else:new_left = (left + 1) % n # 左边指针向右走一步new_right = (right + n - 1) % n# B取过后,A也取较大的# A从左边追溯matrix[left][right] = nums[left] + backtrace(new_left, right)# A从右边追溯,取较大者if nums[right] + backtrace(left, new_right) > matrix[left][right]:matrix[left][right] = nums[right] + backtrace(left, new_right)return matrix[left][right]else:return matrix[left][right]result = 0 # 记录最大结果
i = 0 # n种情况 0 1 2 ... n-1
while True:if i >= n:breakelse:left = (i + n + 1) % nright = (i + n - 1) % nother_sum = backtrace(left, right)if other_sum + nums[i] > result:result = other_sum + nums[i]i += 1
print(result)