参数曲线基本理论
曲线的定义
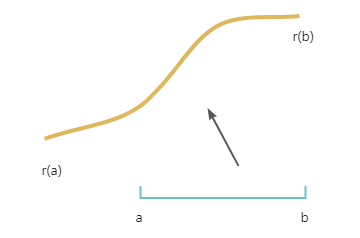
假设有一个运动的质点,从0到T时刻,质点从A点运动到B点,质点运动的轨迹形成了一条曲线,我们可以将这条路径曲线看成是时间 t ∈ [ 0 , T ] t \in [0,T] t∈[0,T]到空间位置 R R R的映射。
映射的概念在参数化曲线曲面中十分重要,通过对这种映射概念的一般化,我们可以定义曲线:一条曲线是一个连续映射函数 f f f,它把一段一维的区间 [ a , b ] [a,b] [a,b]映射到3维空间中, f f f的自变量 t t t称为 f f f的参数, f f f在3维空间中的像就是这条曲线 r ( t ) \boldsymbol r(t) r(t), 可以记为 r ( t ) = ( x ( t ) , y ( t ) , z ( t ) ) \boldsymbol r(t) = (x(t), \ y(t),\ z(t)) r(t)=(x(t), y(t), z(t))
曲线的切向
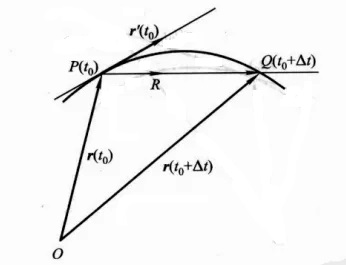
曲线上的每一点都有一个切向量,切向量的数学定义如下
r ′ ( t 0 ) = lim Δ t → 0 r ( t 0 + Δ t ) − r ( t 0 ) Δ t . \mathbf r^{\prime}(t_{0})=\lim_{\Delta t\to0}\frac{\boldsymbol{r}(t_{0}+\Delta t)-\boldsymbol{r}(t_{0})}{\Delta t}. r′(t0)=limΔt→0Δtr(t0+Δt)−r(t0).
根据矢量微积分
r ′ ( t ) = d r d t = ( x ′ ( t ) , y ′ ( t ) , z ′ ( t ) ) \mathbf r'(t) = \frac {d \mathbf r}{dt} = (x'(t), \ y'(t),\ z'(t)) r′(t)=dtdr=(x′(t), y′(t), z′(t))
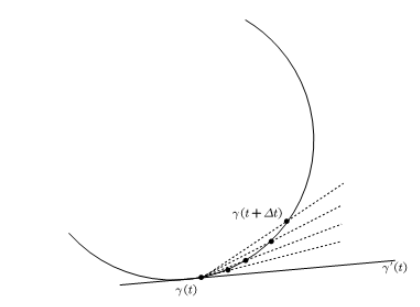
类比于质点的运动轨迹,切向量的物理意义是速度。
注意,切向量是沿切线的向量,而不是曲线上的斜率
如果 r ( t ) \mathbf r(t) r(t)连续可微,且处处 r ′ ( t ) ≠ 0 \mathbf r'(t) \neq 0 r′(t)=0则曲线为正则曲线
r ′ ( t ) = 0 \mathbf r'(t) = 0 r′(t)=0的点称为奇点,可以想象一下,在奇点处速度为0
曲线的长度
曲线的长度即为弧长,计算弧长需要借助一些微积分的知识
d r = r ( t + d t ) − r ( t ) = r ′ ( t ) d t d \mathbf r = \mathbf r(t+dt)- \mathbf r(t)= \mathbf r'(t)dt dr=r(t+dt)−r(t)=r′(t)dt
d s = ∣ d r ∣ ds = |d \mathbf r| ds=∣dr∣
s = ∫ S ∣ r ′ ( t ) ∣ d t s = \int_{S} \mathbf |\mathbf r'(t)| \text{d}t s=∫S∣r′(t)∣dt
r ′ ( t ) = ( x ′ ( t ) , y ′ ( t ) , z ′ ( t ) ) \mathbf r'(t) = (x'(t), \ y'(t),\ z'(t)) r′(t)=(x′(t), y′(t), z′(t))
任意参数区间的弧长为
s a b = ∫ a b ∣ r ′ ( t ) ∣ d t s_{ab} = \int_{a} ^{b} \mathbf |\mathbf r'(t)| \text{d}t sab=∫ab∣r′(t)∣dt
弧长参数化
上面可知,弧长和曲线上的点也是一、一映射的关系,因此可以用弧长作为参数,记为
r ( s ) = ( x ( s ) , y ( s ) , z ( s ) ) \mathbf r(s) = (x(s), \ y(s),\ z(s)) r(s)=(x(s), y(s), z(s))
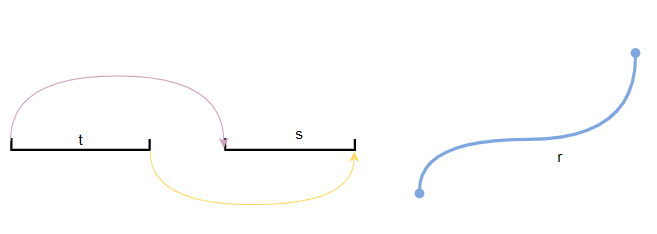
弧长和参数t之间也满足一种映射关系
s = ∫ S ∣ r ′ ( t ) ∣ d t s = \int_{S} \mathbf |\mathbf r'(t)| \text{d}t s=∫S∣r′(t)∣dt,其满足 d s / d t = ∣ r ′ ( t ) ∣ ds/dt = |\boldsymbol r'(t)| ds/dt=∣r′(t)∣
弧长参数化也叫自参数
曲线的弯曲和扭转
可以很直观的看到,不同曲线的弯曲程度是不一样的,同一曲线,在不同的位置弯曲程度也是不一样的,大地看起来是平的,一个圆看起来很弯曲,稍后我们将以曲率来度量曲线的弯曲程度
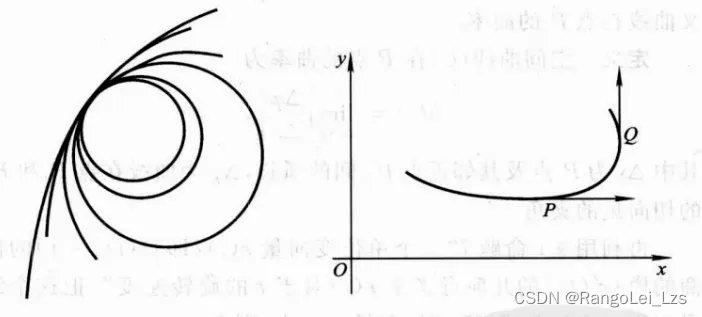
对于复杂的空间曲线,光用曲率显然无法描述曲线的弯曲特性,曲线除了弯曲,还有扭转,稍后我们将以挠率来度量曲线的弯曲程度

密切平面
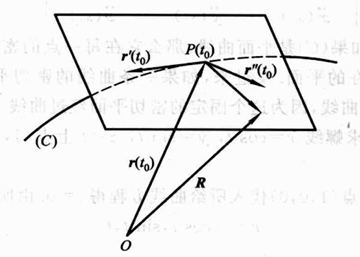
通过一点以及该点切向量的平面有无数多个,其中有一个最贴近曲线的平面,我们称之为密切平面。密切平面的定义,需要用到一些极限的知识,取曲线上P点附近的一个点Q,过直线PQ和P点切向量可以定义一个平面,当Q点趋近于P点时,定义的平面即为密切平面,通过推导可知,密切平面过向量 r ′ ′ ( t ) \mathbf r''(t) r′′(t),因此可以表达为
( R − r ( t 0 ) , r ′ ( t 0 ) , r ′ ′ ( t 0 ) ) = 0 \left(\mathbf{R}-\mathbf{r}(t_{0}),\mathbf{r}^{\prime}(t_{0}),\mathbf{r}^{\prime\prime}(t_{0})\right)=0 (R−r(t0),r′(t0),r′′(t0))=0
Frenet活动标架
弧长参数化和一般参数化之间可以相互转化,弧长参数化有一些优良的性质
弧长参数化下的切向量 r ′ ( s ) = d r d s \boldsymbol{r'}(s) = \frac{d \boldsymbol r}{ds} r′(s)=dsdr
∣ r ′ ( s ) ∣ = ∣ d r d s ∣ = 1 \begin{vmatrix}\boldsymbol{r'}(s)\end{vmatrix}=\begin{vmatrix}\frac{\mathrm{d}\boldsymbol{r}}{\mathrm{d}s}\end{vmatrix}=1 r′(s) = dsdr =1,即线速度为1
r ˙ = d r d s , r ¨ = d 2 r d s 2 \dot{\mathbf r}=\frac{\mathrm{d}\boldsymbol{r}}{\mathrm{d}s},\ddot{\boldsymbol{r}}=\frac{\mathrm{d}^2\boldsymbol{r}}{\mathrm{d}s^2} r˙=dsdr,r¨=ds2d2r
构造单位基矢 α \boldsymbol \alpha α
α = r ˙ = d r d s \boldsymbol \alpha=\dot{ \mathbf r}=\frac{\mathrm{d}\boldsymbol{r}}{\mathrm{d}s} α=r˙=dsdr 由于 α \boldsymbol \alpha α的模长为1,可以得到
α ˙ ⊥ α \dot{\boldsymbol \alpha}\perp \boldsymbol \alpha α˙⊥α r ¨ ⊥ r ˙ \ddot{r}\perp\dot{r} r¨⊥r˙
构造单位基矢 β \boldsymbol \beta β
β = a ˙ ∣ α ˙ ∣ = r ¨ ∣ r ¨ ∣ \boldsymbol \beta =\frac{\dot{a}}{|\dot{\alpha}|}=\frac{\ddot{r}}{|\ddot{r}|} β=∣α˙∣a˙=∣r¨∣r¨
构造单位基矢 γ \boldsymbol \gamma γ
γ = α × β \boldsymbol \gamma=\boldsymbol \alpha\times \boldsymbol \beta γ=α×β
上面构造的三个正交的单位向量,形成frenet标架,可以看到三个基矢的形式非常简单,而且具有很直观的物理意义,他们与密切平面,从切平面,法平面的关系如下图所示:
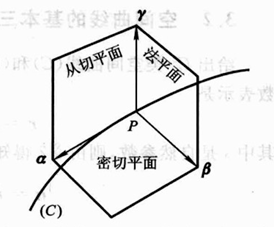
上面公式的形式是弧长参数化的形式,可以转化为任意参数化 r ( t ) \boldsymbol r(t) r(t)的形式
r ′ ( t ) \boldsymbol{r'}(t) r′(t)归一化可以得到 α \boldsymbol \alpha α
r ′ ( t ) \boldsymbol{r'}(t) r′(t)和 r ′ ′ ( t ) \boldsymbol{r''}(t) r′′(t)都在密切平面,因而可以先得到 γ \boldsymbol \gamma γ
关于 r ′ ′ ( t ) \boldsymbol{r''}(t) r′′(t)在密切平面上可以稍作推导:
r ′ = d r d s d s d t = r ˙ d s d t , r ′ ′ = ( r ˙ ) ′ d s d t + r ˙ d 2 s d t 2 = d r ˙ d s ( d s d t ) 2 + r ˙ d 2 s d t 2 = r ¨ ( d s d t ) 2 + r ˙ d 2 s d t 2 , \begin{gathered}\boldsymbol{r}^{\prime}=\frac{\mathrm{d}\boldsymbol{r}}{\mathrm{d}s}\frac{\mathrm{d}s}{\mathrm{d}t}=\dot{\boldsymbol{r}}\frac{\mathrm{d}s}{\mathrm{d}t},\\\boldsymbol{r}^{\prime\prime}=(\dot{\boldsymbol{r}})^{\prime}\frac{\mathrm{d}s}{\mathrm{d}t}+\dot{\boldsymbol{r}}\frac{\mathrm{d}^2s}{\mathrm{d}t^2}=\frac{\mathrm{d}\dot{\boldsymbol{r}}}{\mathrm{d}s}(\frac{\mathrm{d}s}{\mathrm{d}t})^2+\dot{\boldsymbol{r}}\frac{\mathrm{d}^2s}{\mathrm{d}t^2}=\ddot{\boldsymbol{r}}\left(\frac{\mathrm{d}s}{\mathrm{d}t}\right)^2+\dot{\boldsymbol{r}}\frac{\mathrm{d}^2s}{\mathrm{d}t^2},\end{gathered} r′=dsdrdtds=r˙dtds,r′′=(r˙)′dtds+r˙dt2d2s=dsdr˙(dtds)2+r˙dt2d2s=r¨(dtds)2+r˙dt2d2s,
通过 α \boldsymbol \alpha α和 γ \boldsymbol \gamma γ可以得到 β \boldsymbol \beta β
α = r ′ ∣ r ′ ∣ \boldsymbol \alpha=\frac{r^{\prime}}{|r^{\prime}|} α=∣r′∣r′
γ = r ′ × r ′ ′ ∣ r ′ × r ′ ′ ∣ \boldsymbol \gamma=\frac{r^{\prime}\times r^{\prime\prime}}{|r^{\prime}\times r^{\prime\prime}|} γ=∣r′×r′′∣r′×r′′
β = γ × α = ( r ′ ⋅ r ′ ) r ′ ′ − ( r ′ ⋅ r ′ ′ ) r ′ ∣ r ′ ∣ ∣ r ′ × r ′ ′ ∣ \boldsymbol \beta=\boldsymbol \gamma\times \boldsymbol \alpha=\frac{(r^{\prime}\cdot r^{\prime})r^{\prime\prime}-(r^{\prime}\cdot r^{\prime\prime})r^{\prime}}{\mid r^{\prime}\mid\mid r^{\prime}\times r^{\prime\prime}\mid} β=γ×α=∣r′∣∣r′×r′′∣(r′⋅r′)r′′−(r′⋅r′′)r′
曲率和挠率
曲率表示曲线的弯曲程度,其物理意义是切向量对弧长的转动率,即切矢量夹角和弧长增量比值的极限:
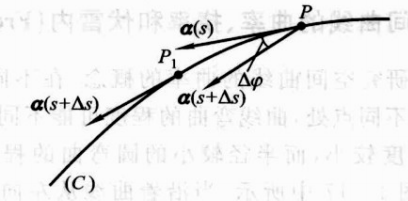
k ( s ) = lim Δ s → 0 ∣ Δ φ Δ s ∣ k(s)=\lim_{\Delta s\to0}\left|\frac{\Delta\varphi}{\Delta s}\right| k(s)=limΔs→0 ΔsΔφ ,为了理解曲率的计算,我们充分利用自然参数下切向量为单位向量的特性:
如下图所示,切向量 α \boldsymbol \alpha α是单位向量,故其对于ds的增量为 d α d\boldsymbol \alpha dα,其模长等于 d θ × 1 d\theta \times1 dθ×1,方向和 α \boldsymbol \alpha α垂直
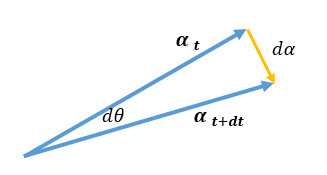
d α d s = d θ n ⃗ d s \frac { d \boldsymbol \alpha } {ds} = \frac { d \theta \vec n }{ds} dsdα=dsdθn
固可以得到:
k ( s ) = d θ d s = ∣ α ˙ ∣ = ∣ r ¨ ∣ k(s)=\frac { d \theta}{ds}=|\dot{\boldsymbol \alpha}| = |\ddot{\boldsymbol r}| k(s)=dsdθ=∣α˙∣=∣r¨∣
同理可以定义挠率为弧长微量变化时,副法向量的夹角和弧长变化的比值:
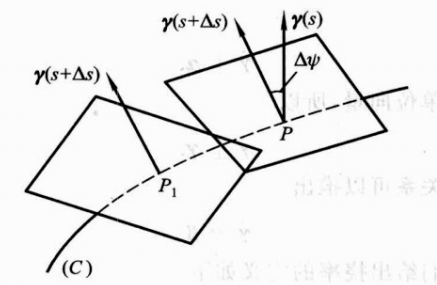
类同曲率推到可得:
∣ γ ˙ ∣ = lim Δ s → 0 ∣ Δ ψ Δ s ∣ , \mid\dot{\boldsymbol{\gamma}}\mid=\lim_{\Delta s\to0}\left|\frac{\Delta\psi}{\Delta s}\right|, ∣γ˙∣=limΔs→0 ΔsΔψ ,
记挠率为:
τ ( s ) = { + ∣ γ ˙ ∣ , 当 γ ˙ 和 β 异向 , − ∣ γ ˙ ∣ , 当 γ ˙ 和 β 同向 . \tau(s)=\begin{cases}+\left|\dot{\boldsymbol{\gamma}}\right|,\text{当}\dot{\boldsymbol{\gamma}}\text{和}\beta {异向,}\\-\left|\dot{\boldsymbol{\gamma}}\right|,\text{当}\dot{\boldsymbol{\gamma}}\text{和}\beta\text{同向}.\end{cases} τ(s)={+∣γ˙∣,当γ˙和β异向,−∣γ˙∣,当γ˙和β同向.
经过微分法则的一些推导,我们可以采用一般参数化来表示曲率,挠率:
κ = ∣ r ′ × r ′ ′ ∣ ∣ r ′ ∣ 3 \kappa=\frac{|\boldsymbol r^{\prime}\times \boldsymbol r^{\prime\prime}|}{| \boldsymbol r^{\prime}|^{3}} κ=∣r′∣3∣r′×r′′∣
τ = ( r ′ , r ′ ′ , r ′ ′ ) ( r ′ × r ′ ′ ) 2 \tau= \frac{(\boldsymbol r^{\prime}, \boldsymbol r^{\prime\prime}, \boldsymbol r^{\prime\prime})}{(\boldsymbol r^{\prime}\times \boldsymbol r^{\prime\prime})^{2}} τ=(r′×r′′)2(r′,r′′,r′′)
曲线论基本:Frenet公式
我们比较关注的是 α \boldsymbol \alpha α, γ \boldsymbol \gamma γ和 β \boldsymbol \beta β对弧长的变化率:
{ α ˙ = k ( s ) β , β ˙ = − k ( s ) α + τ ( s ) γ , γ ˙ = − τ ( s ) β , \begin{cases}\dot{\boldsymbol{\alpha}}=k(s)\boldsymbol{\beta},\\\dot{\boldsymbol{\beta}}=-k(s)\boldsymbol{\alpha}+\tau(s)\boldsymbol{\gamma},\\\dot{\boldsymbol{\gamma}}=-\tau(s)\boldsymbol{\beta},\end{cases} ⎩ ⎨ ⎧α˙=k(s)β,β˙=−k(s)α+τ(s)γ,γ˙=−τ(s)β,
上式的证明也很简单:
β = a ˙ ∣ α ˙ ∣ = r ¨ ∣ r ¨ ∣ \boldsymbol \beta =\frac{\dot{\boldsymbol a}}{|\dot{\boldsymbol \alpha}|}=\frac{\ddot{\boldsymbol r}}{|\ddot{\boldsymbol r}|} β=∣α˙∣a˙=∣r¨∣r¨ 得到 α ˙ = k ( s ) β \dot{\boldsymbol{\alpha}}=k(s)\boldsymbol{\beta} α˙=k(s)β
γ ˙ = ( α × β ) ˙ = α ˙ × β + α × β ˙ = k ( s ) β × β + α × β ˙ = α × β ˙ \dot{\boldsymbol \gamma}=\dot{(\boldsymbol \alpha\times \boldsymbol \beta)}=\dot{\boldsymbol \alpha}\times \boldsymbol \beta+ \boldsymbol \alpha\times\dot{\boldsymbol \beta}=k\left(s\right)\boldsymbol \beta\times\boldsymbol \beta+\boldsymbol \alpha\times\dot{\boldsymbol \beta}=\boldsymbol \alpha\times\dot{\boldsymbol \beta} γ˙=(α×β)˙=α˙×β+α×β˙=k(s)β×β+α×β˙=α×β˙,所以可知 γ ˙ \dot{\boldsymbol \gamma} γ˙垂直于 α \boldsymbol \alpha α
由 γ \boldsymbol \gamma γ是单位向量,可得 γ \boldsymbol \gamma γ垂直于 γ ˙ \dot{\boldsymbol \gamma} γ˙,所以 γ ˙ \dot{\boldsymbol \gamma} γ˙平行于 β \boldsymbol \beta β
{ α ˙ = k ( s ) β , β ˙ = − k ( s ) α + τ ( s ) γ , γ ˙ = − τ ( s ) β , \begin{cases}\dot{\alpha}=k(s)\beta,\\\dot{\beta}=-k(s)\alpha+\tau(s)\gamma,\\ \dot{\gamma}=-\tau(s)\beta,\end{cases} ⎩ ⎨ ⎧α˙=k(s)β,β˙=−k(s)α+τ(s)γ,γ˙=−τ(s)β,
这组公式是空间曲线论的基本公式.它的特点是基本向量 α , β , γ \alpha,\beta,\gamma α,β,γ关于弧长 s 的微商可以用 α , β , γ \alpha,\beta,\gamma α,β,γ的线性组合来表示,它的系数组成反称的方阵
[ 0 k ( s ) 0 − k ( s ) 0 τ ( s ) 0 − τ ( s ) 0 ] \begin{bmatrix}0&k(s)&0\\-k(s)&0&\tau(s)\\0&-\tau(s)&0\end{bmatrix} 0−k(s)0k(s)0−τ(s)0τ(s)0

![[AIGC] MySQL存储引擎详解](https://img-blog.csdnimg.cn/direct/64911e102a9e4c9c9b2f6cfd422c6a60.png)




![[优选算法专栏]专题十五:FloodFill算法(一)](https://img-blog.csdnimg.cn/direct/289224621d034dd38c9b747b4d990236.png)