定点补码加/减法运算
补码加减法的实现
补码加法 : [X + Y] 补 = [X] 补 + [Y] 补和的补码 = 补码的和补码减法 : [X−Y] 补 = [X] 补 + [−Y] 补 = [X] 补 −[Y] 补差的补码 = 补码的差求补公式 : [−Y] 补 = [ [Y] 补 ] 补对 [Y] 补 逐位取反 , 再在最低位加 1
溢出检查(OF)
方法1
溢出逻辑: 正正得负 负负得正
设两数符号位为 ,和数符号位
方法2
符号位进位位,最高位进位位
方法3——双符号位
双符号位的最高位永远是正确符号
二进制加法运算
先考虑一位加法,然后构成加法链。
一位加法:
一位全加器:,
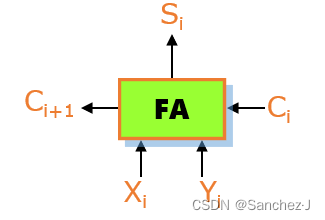
n位加法器:n个一位加法器串联,低位的进位输出连接到高位的进位输入。
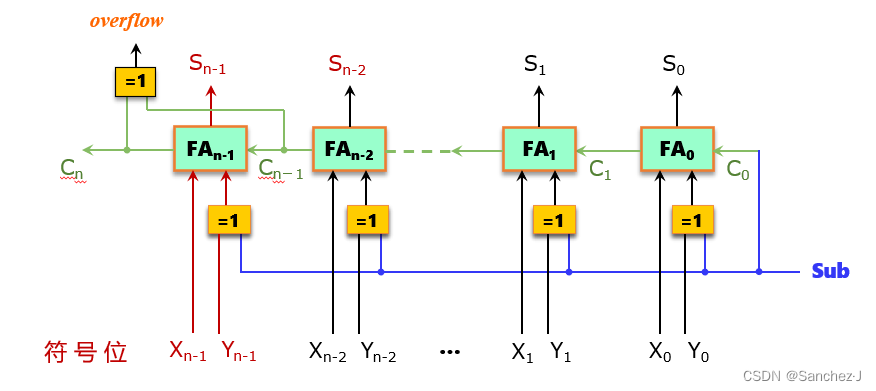
加法器的改造
引入运算控制位,Sub = 0 时作加法,Sub = 1时作减法,此时送入[-Y]补。
标志寄存器
存放运算标志的寄存器,每个标志对应标志寄存器中的一个标志位。
IA-32中的EFLAGS寄存器 (MIPS 无标志寄存器):
ZF(结果为零) SF(结果为负数)
CF(进位/借位) OF(有符号溢出)
并行加法器
串行加法器高位运算需要等待低位运算,延迟过高,因此想要改成并行。
关键在于解决进位对低位运算的依赖。
进位链:
设
(进位生成函数),
(进位传递函数)
则
由递推式可以提前得到进位表达式,使得每一位全加器的进位输入不再依赖前一个全加器。
......
- 进位输出仅与最低位进位输入
有关
- 位数越长,进位链电路复杂度越高
- 通常按照4位一组进行分组运算
定点乘法运算
实现思路
- 执行乘法运算子程序实现乘法运算(软件实现):零成本、RISCV32-I指令集
- 利用加法器多次累加实现乘法运算:原码、补码一位乘法,成本低
- 设置专用乘法器实现乘法运算:成本高
二进制手算乘法

由此可以想到阵列乘法:即先计算相加数,然后逐列相加。用到了很多的全加器,成本高,但换来了效率。

从这种横向进位模式想到,实际上进行的就是:相加➡移位➡相加➡移位......的过程。数学表达出来是这样:
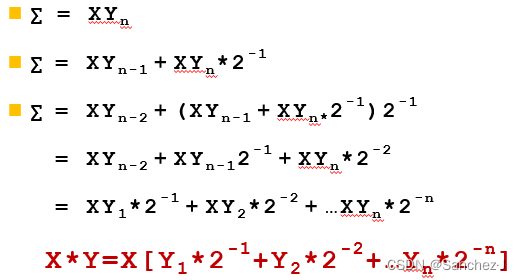
由此可以推出原码乘法
原码乘法
累加后 逻辑右移n 次加法符号位单独计算
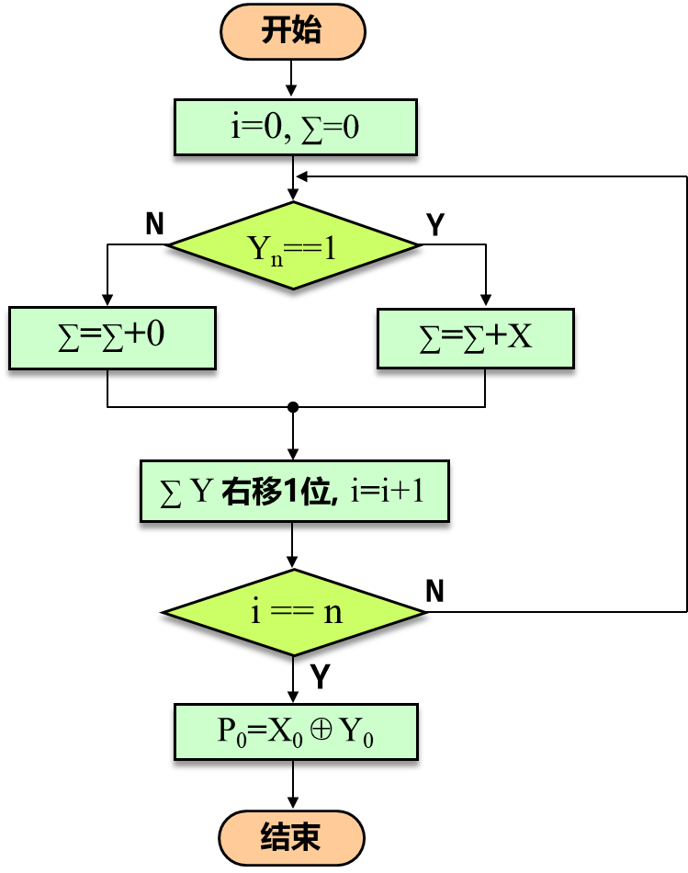
核心运算
- 累加 ∑ = ∑ + 0 或 ∑ = ∑ + X,分支合并为累加 ∑ = ∑ +YnX
- 逻辑右移 ∑ = ∑ / 2
减少寄存器访问∑ = (∑ +YnX)/2先移位再锁存,简化电路,提升速率运算计数控制简单状态机控制,计数器比较
硬件实现:
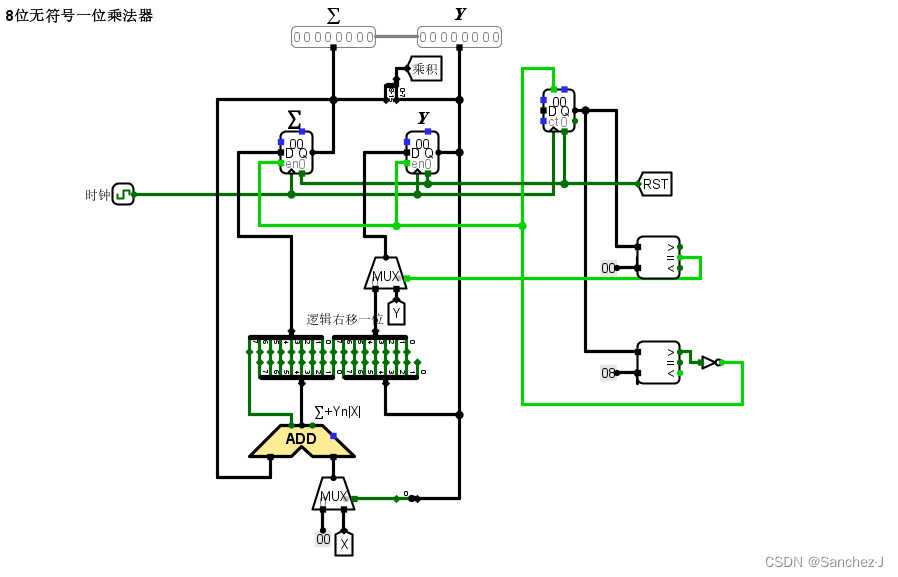
但由于机器内采用补码存储,原码乘法实际上没有什么实际意义 ,但可以通过原码乘法稍作转换推出补码乘法运算方法。
补码乘法
可以推出:[X * Y]补 = [X]补 * 0.Y1Y2…Yn – Y0[X]补 (Y0为符号位)
进一步有:[X * Y]补 = [X]补 * [ Y1 - Y0 + (Y2 - Y1)2^-1 + (Y3 - Y2)2^-2+…+(0-Yn)2^-n ]
可以看出和原码乘法形式非常类似,因此可以改进原码乘法来实现。
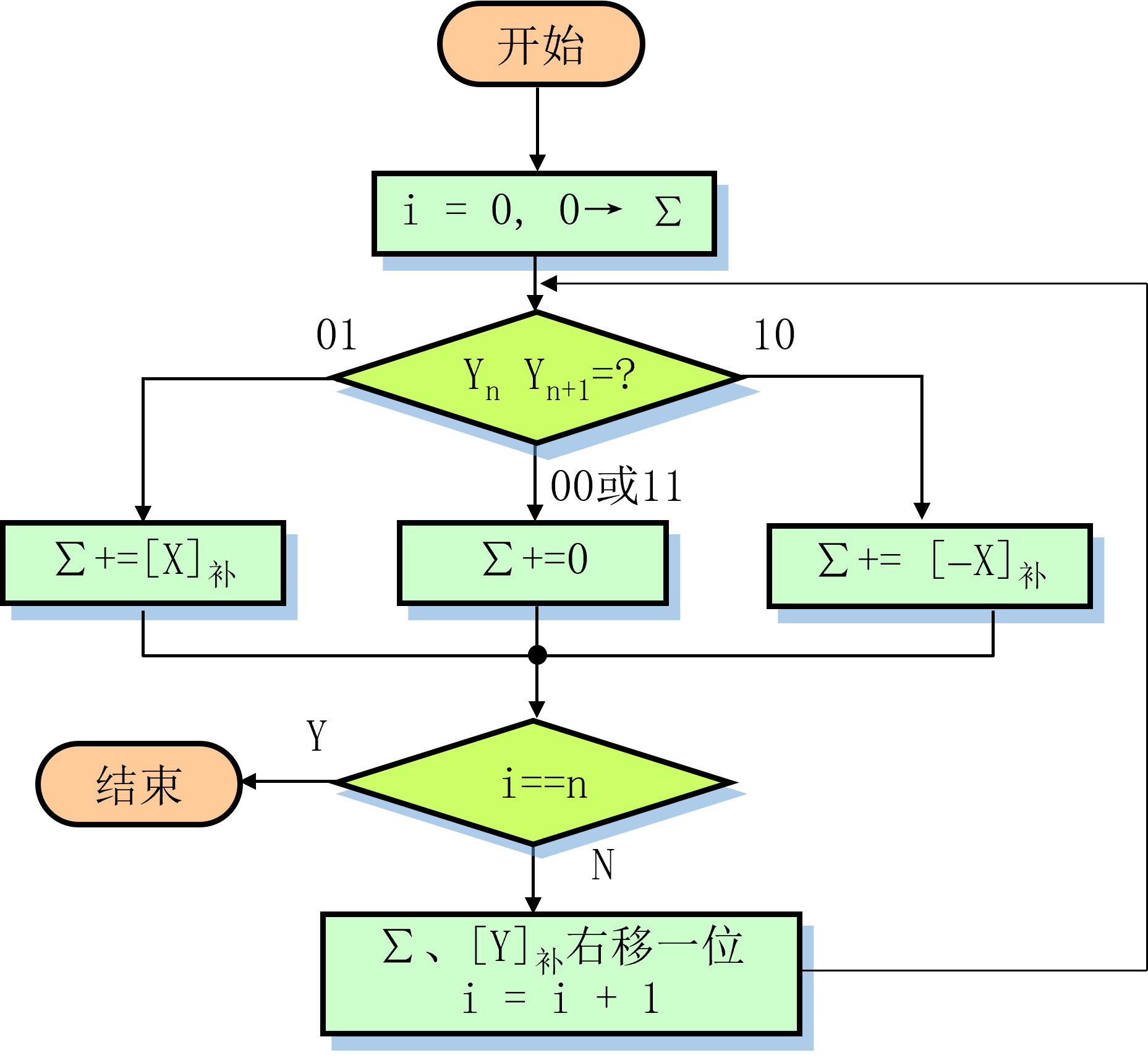
n+1 次加法, n 次 算术右移符号位参与运算, 不需单独计算符号位
硬件实现:
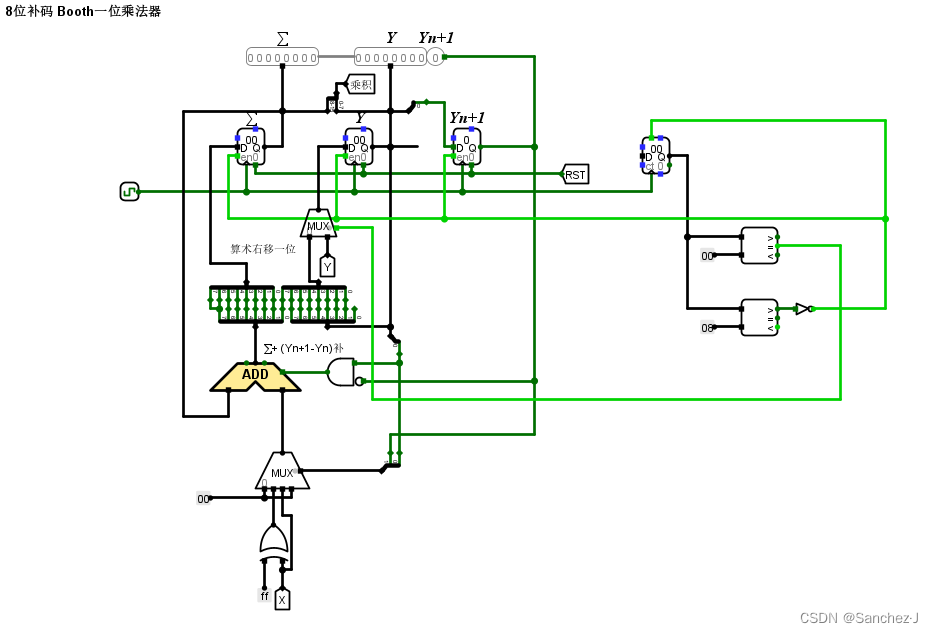
阵列乘法
再回看阵列乘法
- 符号单独运算:直接异或
- 绝对值相乘:仅需考虑数值部分的计算
- R=X*Y
1 × 1 = 1
1 × 0 = 0
0 × 1 = 0
0 × 0 = 0
- 与门实现一位乘法
- 25个与门并发
- 一级门延迟,生成所有相加数

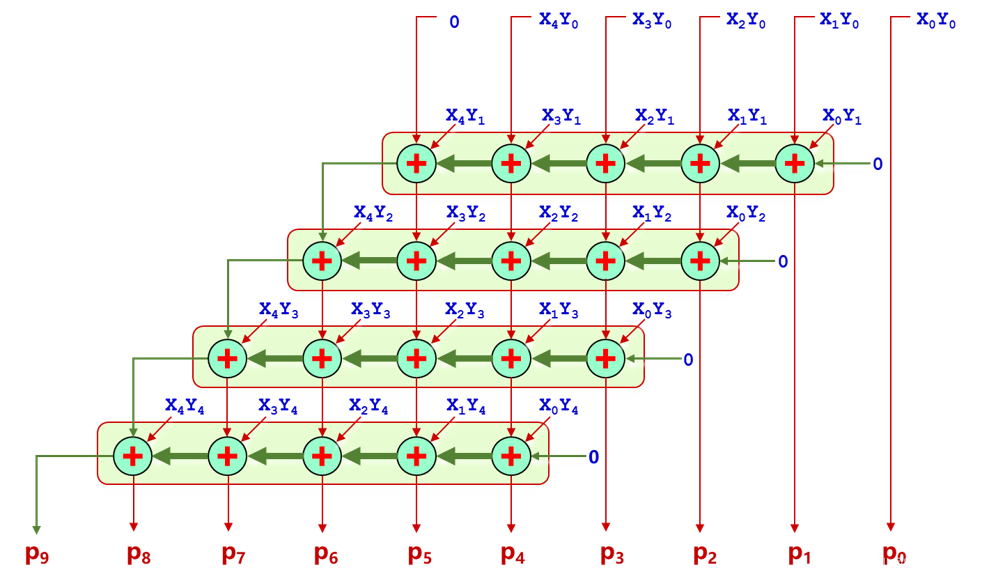
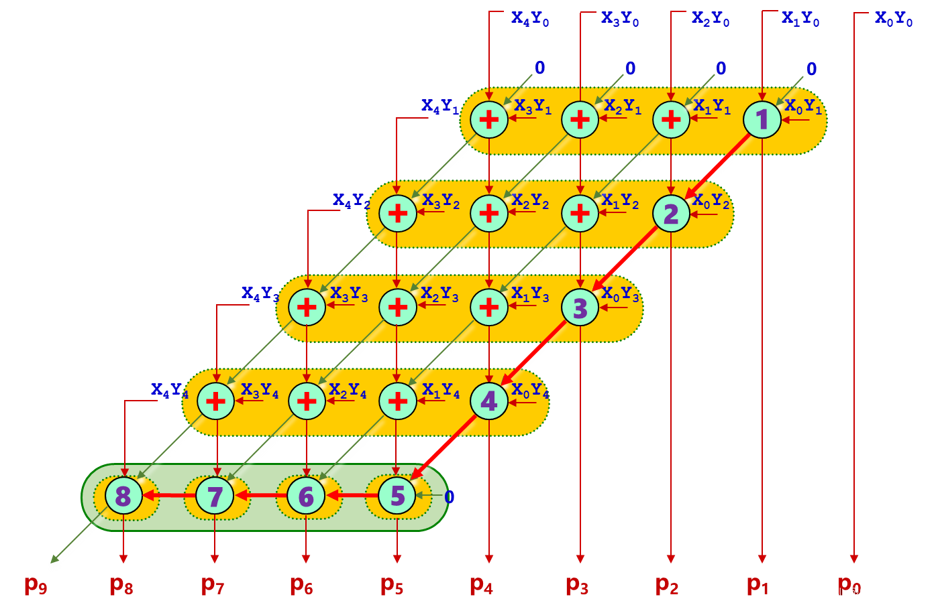
不同的进位方式延迟不同,主要有横向进位、斜向进位两种。



![[Qt] QString::fromLocal8Bit 的使用误区](https://img-blog.csdnimg.cn/direct/62600f6b003a467495d5f47db140b1b2.png)