6. 计算机的运算方法
文章目录
- 6. 计算机的运算方法
- 6.1 机器数的表示
- 6.1.1 无符号数和有符号数
- 6.1.2 有符号数-原码
- 6.1.3 有符号数-补码
- 6.1.4 有符号数-反码
- 6.1.5 有符号数-移码
- 6.1.6 原码、补码、反码的比较
- 6.2 数的定点表示和浮点表示
- 6.2.1 定点表示
- 6.2.2 浮点表示
- 6.2.3 ΔIEEE 754标准
- 6.3 定点运算
- 6.3.1 移位运算
- 6.3.2 加减法运算-补码
- 6.3.3 Δ乘法运算-原码
- 6.3.4 Δ乘法运算-补码
- 6.3.5 除法运算-原码
- 6.3.6 Δ除法运算-补码
- 6.4 浮点四则运算
- 6.4.1 浮点数的加减运算
- 6.4.2 Δ浮点数的乘除运算
- 6.4.3 Δ浮点运算的硬件配置
- 6.5 算术逻辑单元
- 6.5.1 ALU电路
- 6.5.2 快速进位链
- 本笔记参考哈工大刘宏伟老师的MOOC《计算机组成原理(上)_哈尔滨工业大学》、《计算机组成原理(下)_哈尔滨工业大学》。
- 或者是B站《计算机组成原理(哈工大刘宏伟)135讲(全)高清》,大家一起听比较热闹。
- 中文教材:《计算机组成原理(第二版)-唐朔飞.pdf》、《学习指导与习题解答(第2版)-唐朔飞.pdf》
- 本篇笔记对应课程第六章(下图加粗)。
本章全是重点😅,Δ表示笔记补充了MOOC没有讲到的内容。
本章重点:
- 计算机中数的表示【6.1、6.2】:介绍能够被硬件直接识别和处理的数据类型。也就是计算机指令中,包含对这些数据类型进行处理的指令,所以必须用硬件来实现这些运算。
- 计算机的运算方法【6.3、6.4】:整体思路就是对笔算方法进行改进,主要关心硬件可实现。
- 运算器的设计【6.5】:介绍CPU中的算术逻辑运算单元ALU的电路设计。
6.1 机器数的表示
6.1.1 无符号数和有符号数
我们平常手写的有符号数被称为“真值”,而“机器数”则是数字在计算机中的表示方法。“无符号数”就是没有正负号的整数(默认正数),只需要将无符号数用二进制表示,即可按位存储到寄存器中。寄存器的位数反映无符号数的表示范围,比如8位寄存器的取值范围就是 0 ∼ 255 0\sim 255 0∼255 (C语言char)、16位寄存器的取值范围就是 0 ∼ 65535 0\sim 65535 0∼65535 (C语言unsigned short)、32位寄存器的取值范围就是 0 ∼ 2 32 − 1 0\sim 2^{32}-1 0∼232−1 (C语言unsigned int)。
有符号数包括“符号部分”、“数值部分”,将“符号部分”的正负号进行数字化表示,然后和“数值部分”分别保存到寄存器中,就是“机器数”。通常使用最高位表示“符号位”,也就是将寄存器的最高位作为符号位,“0”就表示为“正号+”、“1”就表示为“负号-”。下图给出“真值”和“机器数”的关系:
- 符号位:默认为机器数的最高位,0表示正、1表示负。
- 数值部分:机器中没有硬件表示小数点,只靠约定。比如对于纯小数来说,符号位后面就是小数点。
- 位数:寄存器长度有限,所以机器数会受到存储字长的限制。
注:本节只考虑有符号的 整数 和 绝对值小于1的小数。绝对值比1大的小数(如“ 8.4 8.4 8.4”),将在下一节“6.2节-数的定点表示和浮点表示”再进行介绍。
下面介绍四种机器数:原码、反码、补码、移码。主要关心:
- 机器数与真值的转换。
- 不同机器数形式之间的转化。
- 机器数表示的范围与其字长的关系。
6.1.2 有符号数-原码

将数值部分写成二进制形式、符号位使用0/1表示就是“原码”,也就是“带符号的绝对值表示”。上面直接给出原码表示法的计算公式,但实际上,上述计算公式是根据下面的思想反推出来的!比如下面直接给出二进制数,写出其原码:
整数:用 逗号 将“符号位”和“数值部分”隔开。
- x = + 1110 ⟶ [ x ] 原 = 0 , 1110 x=+1110 \longrightarrow [x]_{原}=0,1110 x=+1110⟶[x]原=0,1110
- x = − 1110 ⟶ [ x ] 原 = 1 , 1110 = 推导公式 1 , 0000 + 0 , 1110 x=-1110 \longrightarrow [x]_{原}=1,1110\xlongequal{推导公式}1,0000+0,1110 x=−1110⟶[x]原=1,1110推导公式1,0000+0,1110
小数:用 小数点 将“符号位”和“数值部分”隔开。
- x = + 0.1101 ⟶ [ x ] 原 = 0.1101 x=+0.1101 \longrightarrow [x]_{原}=0.1101 x=+0.1101⟶[x]原=0.1101,注意前面的“0”表示数值大小,后面原码的“0”表示正负号。
- x = − 0.1101 ⟶ [ x ] 原 = 1.1101 = 推导公式 1.0000 + 0.1101 x=-0.1101 \longrightarrow [x]_{原}=1.1101\xlongequal{推导公式}1.0000+0.1101 x=−0.1101⟶[x]原=1.1101推导公式1.0000+0.1101
注:假设数值部分为4位。
来看几个例子:
注:下面均假设数值部分为4位。
【例6.1】已知 [ x ] 原 = 1.0011 [x]_{原}=1.0011 [x]原=1.0011,求 x x x?
解:由定义得 x = 1 − [ x ] 原 = 1 − 1.0011 = − 0.0011 x=1-[x]_{原}=1-1.0011=-0.0011 x=1−[x]原=1−1.0011=−0.0011【例6.2】已知 [ x ] 原 = 1 , 1100 [x]_{原}=1,1100 [x]原=1,1100,求 x x x?
解:由定义得 x = 2 4 − [ x ] 原 = 10000 − 1 , 1100 = − 1100 x=2^4-[x]_{原}=10000-1,1100=-1100 x=24−[x]原=10000−1,1100=−1100【例6.3】已知 [ x ] 原 = 0.1101 [x]_{原}=0.1101 [x]原=0.1101,求 x x x?
解:因为原码符号位为0,表示为正数,所以直接 x = + 0.1101 x=+0.1101 x=+0.1101【例6.4】求 x = 0 x=0 x=0 的原码?
解:对于小数来说, [ + 0.0000 ] 原 = 0.0000 [+0.0000]_{原}=0.0000 [+0.0000]原=0.0000、 [ − 0.0000 ] 原 = 1.0000 [-0.0000]_{原}=1.0000 [−0.0000]原=1.0000。
对于整数来说, [ + 0 ] 原 = 0 , 0000 [+0]_{原}=0,0000 [+0]原=0,0000、 [ − 0 ] 原 = 1 , 0000 [-0]_{原}=1,0000 [−0]原=1,0000。
即,“+0”和“-0”的原码不同!
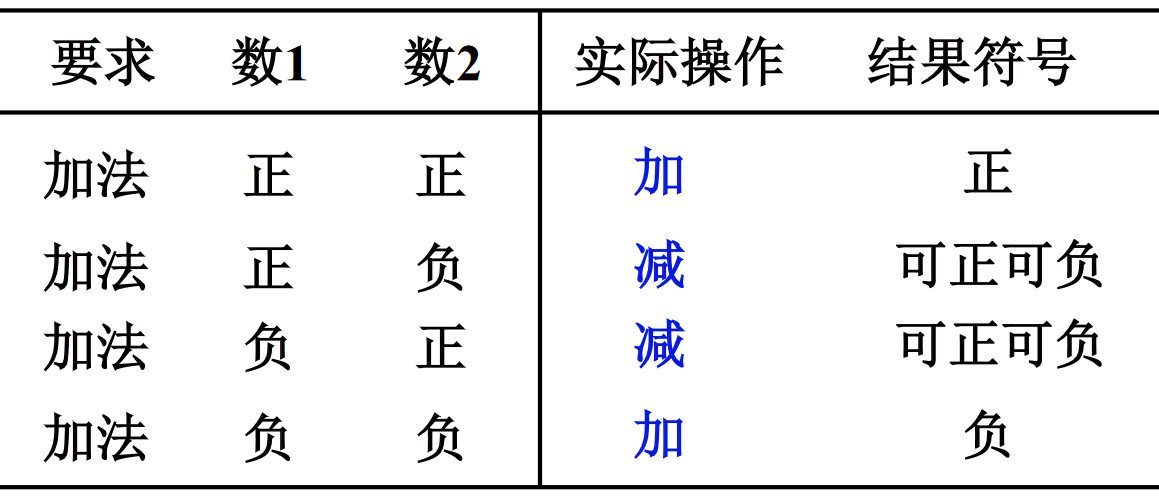
原码的特点就是简单、直观。但是用原码作加法时,两个操作数符号不同时,本质上还是要执行减法(如上图)。此时就希望找到一个与负数等价的正数来代替这个负数,使“减”转化成“加”,也就是“补码”。
6.1.3 有符号数-补码

“补”这个概念来自于时钟,比如想将6点时钟拨成3点,那么可以逆时针-3小时、或者顺时针+9小时(因为时钟要对12取模),也就是“-3”和“+9”等价!于是 “补码”就是与负数等价的正数,根本思想为,一个正数和一个负数互为补数时,它们绝对值之和即为模数。正数的补数即为其本身,负数加上模数则为其补数。但实际负数的补码,可用原码除符号位外每位取反,末位加1求得。也就是,正数的补码为其自身,负数的补码=反码+1。如下:
整数:用逗号将“符号位”和“数值部分”隔开。
- x = + 1010 ⟶ [ x ] 补 = 0 , 1010 x=+1010 \longrightarrow [x]_{补}=0,1010 x=+1010⟶[x]补=0,1010
- x = − 1010 ⟶ [ x ] 补 = 10000 + ( − 1110 ) = 1 , 0110 = 发现规律 1 , ( 0101 + 0001 ) = [ x ] 反 + 1 x=-1010 \longrightarrow [x]_{补}=10000+(-1110)=1,0110\xlongequal{发现规律}1,(0101+0001)=[x]_{反}+1 x=−1010⟶[x]补=10000+(−1110)=1,0110发现规律1,(0101+0001)=[x]反+1
小数:用小数点将“符号位”和“数值部分”隔开。
- x = + 0.1110 ⟶ [ x ] 补 = 0.1110 x=+0.1110 \longrightarrow [x]_{补}=0.1110 x=+0.1110⟶[x]补=0.1110,注意前面的“0”表示数值大小,后面原码的“0”表示正负号。
- x = − 0.1110 ⟶ [ x ] 补 = 10.0000 + ( − 1.0010 ) = 1.0010 = 发现规律 1. ( 0001 + 0001 ) = [ x ] 反 + 1 x=-0.1110 \longrightarrow [x]_{补}=10.0000+(-1.0010)=1.0010\xlongequal{发现规律}1.(0001+0001)=[x]_{反}+1 x=−0.1110⟶[x]补=10.0000+(−1.0010)=1.0010发现规律1.(0001+0001)=[x]反+1
下面给出几个例子:
【例6.5】已知 [ x ] 补 = 0.0001 [x]_{补}=0.0001 [x]补=0.0001,求 x x x?
解:正数的补码为其自身,显然 x = + 0.0001 x=+0.0001 x=+0.0001。【例6.6】已知 [ x ] 补 = 1.0001 [x]_{补}=1.0001 [x]补=1.0001,求 x x x?
解:由定义得 x = [ x ] 补 − 2 = − ( 10.0000 − 1.0001 ) = − 0.1111 x=[x]_{补}-2=-(10.0000-1.0001)=-0.1111 x=[x]补−2=−(10.0000−1.0001)=−0.1111。或者直接 x = [ 1.0001 − 0.0001 ] 反 = − 0.1111 x=[1.0001-0.0001]_{反}=-0.1111 x=[1.0001−0.0001]反=−0.1111,非常便捷。【例6.7】已知 [ x ] 补 = 1 , 1110 [x]_{补}=1,1110 [x]补=1,1110,求 x x x?
解:可以由公式反推,也可以直接 x = 1 , [ 1110 − 0001 ] 反 = − 0010 x=1,[1110-0001]_{反}=-0010 x=1,[1110−0001]反=−0010【自定义例】求 0 0 0 的补码?
解:对于小数来说, [ + 0.0000 ] 补 = 0.0000 [+0.0000]_{补}=0.0000 [+0.0000]补=0.0000、 [ − 0.0000 ] 补 = 1.1111 + 0.0001 = 0.0000 [-0.0000]_{补}=1.1111+0.0001=0.0000 [−0.0000]补=1.1111+0.0001=0.0000。
对于整数来说, [ + 0 ] 补 = 0 , 0000 [+0]_{补}=0,0000 [+0]补=0,0000、 [ − 0 ] 补 = 1 , 1111 + 0 , 0001 = 0 , 0000 [-0]_{补}=1,1111+0,0001=0,0000 [−0]补=1,1111+0,0001=0,0000。
即,“+0”和“-0”的补码相同!【自定义例】 求真值 − 1.0000 -1.0000 −1.0000 的补码?求补码 [ x ] 补 = 1 , 0000 [x]_{补}=1,0000 [x]补=1,0000 对应的真值?
解:由小数补码的定义得 [ x ] 补 = 2 + x = 10.0000 − 1.0000 = 1.0000 [x]_{补} = 2+x=10.0000-1.0000=1.0000 [x]补=2+x=10.0000−1.0000=1.0000。原码无法表示 − 1.0000 -1.0000 −1.0000!
由正数补码的定义得 x = [ x ] 补 − 2 5 = − ( 10 , 0000 − 1 , 0000 ) = − 1 , 0000 = − 2 5 x=[x]_{补}-2^5=-(10,0000-1,0000)=-1,0000=-2^5 x=[x]补−25=−(10,0000−1,0000)=−1,0000=−25。
即,只有符号位是1的补码,表示取值范围内最小的幂次!
6.1.4 有符号数-反码
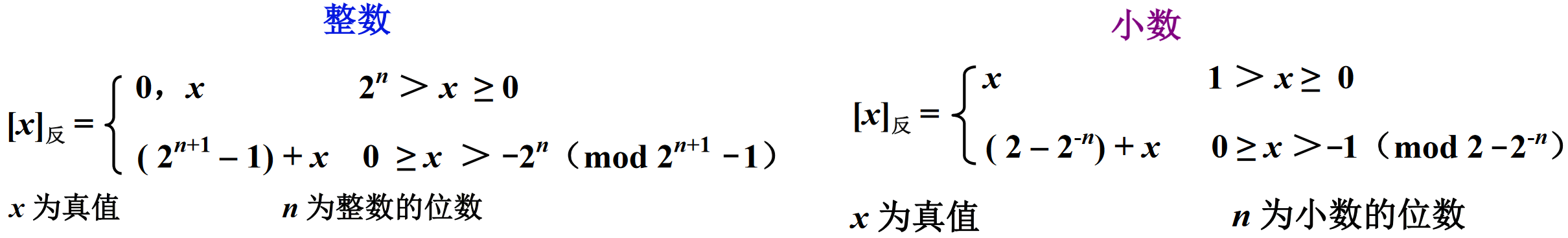
反码很简单,就是正数的反码为其自身,负数的反码将其“原码”的“数值部分”按位取反、“符号位”不变。如下:
整数:用逗号将“符号位”和“数值部分”隔开。
- x = + 1101 ⟶ [ x ] 反 = 0 , 1101 x=+1101 \longrightarrow [x]_{反}=0,1101 x=+1101⟶[x]反=0,1101
- x = − 1101 ⟶ [ x ] 反 = 1 , 0010 x=-1101 \longrightarrow [x]_{反}=1,0010 x=−1101⟶[x]反=1,0010
小数:用小数点将“符号位”和“数值部分”隔开。
- x = + 0.1101 ⟶ [ x ] 反 = 0.1101 x=+0.1101 \longrightarrow [x]_{反}=0.1101 x=+0.1101⟶[x]反=0.1101,注意前面的“0”表示数值大小,后面原码的“0”表示正负号。
- x = − 0.1010 ⟶ [ x ] 反 = 1.0101 x=-0.1010 \longrightarrow [x]_{反}=1.0101 x=−0.1010⟶[x]反=1.0101
【例6.8】已知 [ x ] 反 = 0 , 1110 [x]_{反}=0,1110 [x]反=0,1110,求 x x x?
解:由定义得 x = + 1110 x=+1110 x=+1110【例6.9】已知 [ x ] 反 = 1 , 1110 [x]_{反}=1,1110 [x]反=1,1110,求 x x x?
解:由定义得 x = − 0001 x=-0001 x=−0001【例6.10】求 0 0 0 的反码?
解:对于小数来说, [ + 0.0000 ] 反 = 0.0000 [+0.0000]_{反}=0.0000 [+0.0000]反=0.0000、 [ − 0.0000 ] 反 = 1.1111 [-0.0000]_{反}=1.1111 [−0.0000]反=1.1111。
对于整数来说, [ + 0 ] 反 = 0 , 0000 [+0]_{反}=0,0000 [+0]反=0,0000、 [ − 0 ] 反 = 1 , 1111 [-0]_{反}=1,1111 [−0]反=1,1111。
即,“+0”和“-0”的反码不同!
6.1.5 有符号数-移码

如上图,补码表示很难直接判断其真值大小。单纯从寄存器的角度看,不仅所有的负数都比正数大,就连负数也是按照逆序排序的。于是很自然的就想到直接将补码的符号位取反不就可以了!于是给出移码的定义,如下:
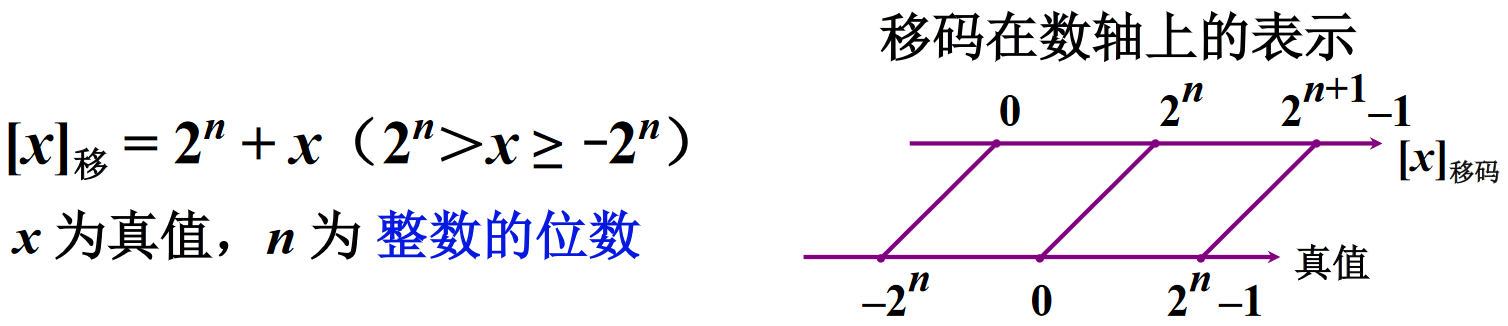
移码和补码的比较
- x = + 1100100 ⟶ [ x ] 补 = 0 , 1100100 [ x ] 移 = 1 , 1100100 x=+1100100 \longrightarrow [x]_{补}=0,1100100\quad [x]_{移}=1,1100100 x=+1100100⟶[x]补=0,1100100[x]移=1,1100100
- x = − 1100100 ⟶ [ x ] 补 = 1 , 0011100 [ x ] 移 = 0 , 0011100 x=-1100100 \longrightarrow [x]_{补}=1,0011100\quad [x]_{移}=0,0011100 x=−1100100⟶[x]补=1,0011100[x]移=0,0011100
移码的特点:
- “补码”与“移码”符号位相反。两者的转换非常简单。
- 不区分正数和负数。“+0”和“-0”的移码相同!
- 小数没有移码。在计算机中,“移码”专用于判断,通常用于“浮点数”的阶码部分,所以没有小数的移码定义。
- 最小真值的移码为全0。根据第一条,最小真值的补码只有符号位为1。
6.1.6 原码、补码、反码的比较
下图给出了“原码”、“补码”、“反码”的转换关系:
正数的机器数都与原码相同,负数有如下转换关系:
- 【原码–>反码】除符号位外每位取反。
- 【反码–>补码】末位加1。
- 【原码–>补码】除符号位外每位取反、末位加1。
- 【补码–>原码】除符号位外每位取反、末位加1。
注意:【原码–>补码】和【补码–>原码】的转换逻辑相同!
下面给出两个例子:
【例6.11】设机器数字长为8位(其中1位为符号位)。对于整数,当其分别代表无符号数、原码、补码和反码时,对应的真值范围各为多少?
即,补码比原码、反码可以多表示一个负数。
【例6.12】 已知 [ y ] 补 [y]_{补} [y]补,求 [ − y ] 补 [-y]_{补} [−y]补?
解:将 [ y ] 补 [y]_{补} [y]补 连同符号位在内,每位取反,末位加1,即为 [ − y ] 补 [-y]_{补} [−y]补。这是一个非常重要的规律。
6.2 数的定点表示和浮点表示
6.2.1 定点表示

“定点表示”也就是小数点位置固定,要么在第一位后表示“绝对值小于1的小数”,要么在最后一个表示“整数”。上一节已经详细的介绍了。于是在定点机中可以分为如下两种。其中“小数定点机”精度为 2 − n 2^{-n} 2−n、“整数定点机”的精度为 1 1 1,下表给出了取值范围:

但“定点表示”有很多问题,于是便有了下一小节的“浮点表示”:
- 编程困难,程序员要调节小数点的位置。
- 数的表示范围小,为了能表示两个大小相差很大的数据,需要很长的机器字长。比如太阳的质量是 0.2 × 1 0 34 0.2\times 10^{34} 0.2×1034 克,一个电子的质量大约为 0.9 × 1 0 − 27 0.9\times 10^{-27} 0.9×10−27 克,两者数量级相差 1 0 61 10^{61} 1061,使用定点表示则相差203位。
- 数据存储单元的利用率往往很低。
6.2.2 浮点表示
下面是本小节关心的问题:
- 为什么在计算机中要引入浮点数表示?——定点表示不够用
- 浮点表示的格式是什么?
- 尾数和阶码的基值必须是2吗?基值的影响?——不一定,但影响表示精度
- 表数范围与精度和哪些因素有关?
- 为什么要引入规格化表示?
- 目前浮点数表示格式的标准是什么?——IEEE 754
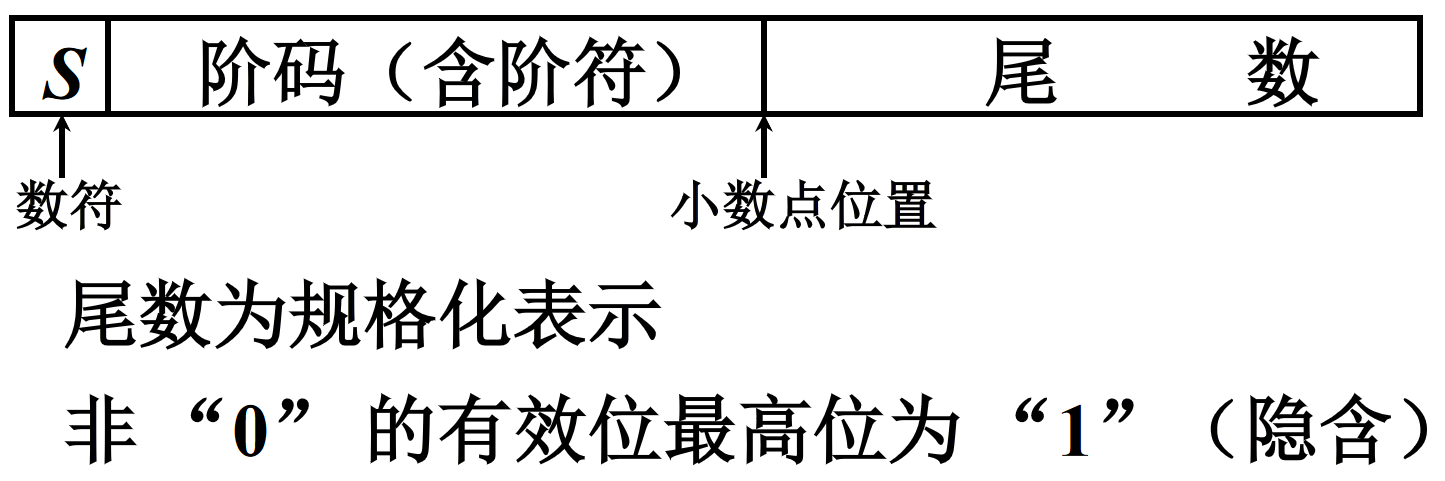
“浮点表示”的基本思想就是使用 二进制的“科学记数法”,比如 N = 11.0101 = 0.110101 × 2 [ 10 ] 二进制 N=11.0101=0.110101\times 2^{[10]_{二进制}} N=11.0101=0.110101×2[10]二进制,注意幂次也是二进制数(规格化数)。由于幂次的阶码本身也是二进制表示,所以幂次的范围很大,这样我们便可以使用有限字长表示数量级相差很大的数字。下面给出浮点数的规格化形式:

- j j j:阶码,是一个有符号整数,控制尾数的左右移动。 j f j_f jf 是符号位、其余是数值部分(长度为 m m m)。
- S S S:尾数,是绝对值小于1的小数、要求尾数规格化。 S f S_f Sf 是符号位、其余为数值部分(长度为 n n n)。
- r r r:尾数的基值,计算机中通常取 2、4、8、16等。基数 r r r 越大,可表示的浮点数的范围越大,但浮点数的精度降低,因为一次移动的位数增加。基数不同,浮点数的规格化形式不同,如下。
- r = 2 r=2 r=2,“原码规格化”原则是尾数最高位为1;“补码规格化”原则是尾数的符号位和第一数位不同。
- r = 4 r=4 r=4,“原码规格化”原则尾数最高2位不全为0。
- r = 8 r=8 r=8,“原码规格化”原则尾数最高3位不全为0。
注:规格化是为了尽可能保证数据精度,防止存储很多无效0。
浮点数本质上是用用有限的数据表示无限多的实数。显然浮点数的表示范围和 阶码 j j j、尾数 S S S 的取值范围有关。阶码长度影响范围,尾数长度影响精度。如下图,可以看到 m = 4 m=4 m=4、 n = 10 n=10 n=10 的浮点数(16位),表示范围为 ± [ 2 − 25 ∼ 2 15 ) \pm[2^{-25}\sim2^{15}) ±[2−25∼215)、精度为 2 − 10 2^{-10} 2−10(十进制):

- 上溢:阶码>最大阶码,按“计算出错”处理。
- 下溢:尾数为0、或者阶码<最小阶码,按“机器零”处理。机器零的两种情况:
- 浮点数尾数=0时。
- 浮点数阶码≤能表示的最小数时。若阶码采用“补码”,最小值是只有最高位为1;若阶码采用“移码”,最小值是阶码全是0。
注:上述机器零的规定有利于机器中“判0”电路的实现。
下面是几个浮点数范围的练习:
【练习】设机器数字长为24位,欲表示±3万的十进制数,试问在保证数的最大精度的前提下,除阶符、数符各取1位外,阶码、尾数各取几位?
解:由 2 14 < 30000 < 2 15 2^{14}<30000<2^{15 } 214<30000<215,阶码取值范围应大于15,于是阶码长度最小为 4 + 1 = 5 4+1=5 4+1=5 位。剩下的19位就是尾数长度。【例6.13】将 + 19 128 +\frac{19}{128} +12819 写成二进制定点数、浮点数及在定点机和浮点机中的机器数形式。其中数值部分均取10位,数符取1位,浮点数阶码取5位(含1位阶符),尾数规格化。
解:二进制定点数: x = + 19 128 = 10011 × 2 − [ 7 ] 十进制 = 0.00100 11000 x=+\frac{19}{128}=10011\times2^{-[7]_{十进制}}=0.00100\;11\bold{000} x=+12819=10011×2−[7]十进制=0.0010011000。
浮点数的规格化形式 x = 0.10011 00000 × 2 − [ 10 ] 二进制 x=0.10011\;00000\times 2^{-[10]_{二进制}} x=0.1001100000×2−[10]二进制。
定点机: [ x ] 原 = [ x ] 反 = [ x ] 补 = 0.00100 11000 [x]_{原}=[x]_{反}=[x]_{补}=0.00100\;11000 [x]原=[x]反=[x]补=0.0010011000。
浮点机(原码):阶码为 j = 1 , 0010 j=1,0010 j=1,0010、尾数为 0.10011 00000 0.10011\;00000 0.1001100000。
浮点机(反码):阶码为 j = 1 , 1101 j=1,1101 j=1,1101、尾数为 0.10011 00000 0.10011\;00000 0.1001100000。
浮点机(补码):阶码为 j = 1 , 1110 j=1,1110 j=1,1110、尾数为 0.10011 00000 0.10011\;00000 0.1001100000。【例6.14】将 − 58 -58 −58 表示成二进制定点数和浮点数,并写出它在定点机和浮点机中的三种机器数及阶码为移码、尾数为补码的形式(其他要求同上例)。
解:二进制定点数: x = − 111010 = − 00001 11010 x=-111010=-\bold{0000}1\;11010 x=−111010=−0000111010。
浮点数的规格化形式 x = − 0.11101 00000 × 2 + [ 110 ] 二进制 x=-0.11101\;00000\times 2^{+[110]_{二进制}} x=−0.1110100000×2+[110]二进制。
定点机(原码): [ x ] 原 = 1 , 00001 11010 [x]_{原}=1,00001\;11010 [x]原=1,0000111010。
定点机(反码): [ x ] 反 = 1 , 11110 00101 [x]_{反}=1,11110\;00101 [x]反=1,1111000101。
定点机(补码): [ x ] 补 = 1 , 11110 00110 [x]_{补}=1,11110\;00110 [x]补=1,1111000110。
浮点机(原码):阶码为 j = 0 , 0110 j=0,0110 j=0,0110、尾数为 1.11101 00000 1.11101\;00000 1.1110100000。
浮点机(反码):阶码为 j = 0 , 0110 j=0,0110 j=0,0110、尾数为 1.00010 11111 1.00010\;11111 1.0001011111。
浮点机(补码):阶码为 j = 0 , 0110 j=0,0110 j=0,0110、尾数为 1.00011 00000 1.00011\;00000 1.0001100000。
浮点机(要求):阶码为 j = 1 , 0110 j=1,0110 j=1,0110、尾数为 1.00011 00000 1.00011\;00000 1.0001100000。【习题6.16】设机器数字长为16位,写出下列各种情况下它能表示的数的范围。设机器数采用1位符号位,答案均用十进制数表示。
(1) 无符号数。—— 0 ∼ 65535 0\sim 65535 0∼65535。
(2) 原码表示的定点小数。—— − ( 1 − 2 − 15 ) ∼ 1 − 2 − 15 -(1-2^{-15})\sim1-2^{-15} −(1−2−15)∼1−2−15
(3) 补码表示的定点小数。—— − 1 ∼ 1 − 2 − 15 -1\sim1-2^{-15} −1∼1−2−15
(4) 补码表示的定点整数。—— − 32768 ∼ 32767 -32768\sim32767 −32768∼32767
(5) 原码表示的定点整数。—— − 32767 ∼ 32767 -32767\sim32767 −32767∼32767
(6) 浮点数的格式为:阶码6位(含1位阶符),尾数10位(含1位数符)。分别写出正数和负数的表示范围。(假设阶码和尾数都是原码、且不用规格化)
原码非规格化:正数 2 − 9 × 2 − 31 ∼ ( 1 − 2 − 9 ) × 2 31 2^{-9}\times2^{-31}\;\sim\;(1-2^{-9})\times 2^{31} 2−9×2−31∼(1−2−9)×231;负数 − ( 1 − 2 − 9 ) × 2 31 ∼ − 2 − 9 × 2 − 31 -(1-2^{-9})\times 2^{31}\;\sim\;-2^{-9}\times2^{-31} −(1−2−9)×231∼−2−9×2−31。
(7) 浮点数格式同(6),机器数采用补码规格化形式,分别写出其对应的正数和负数的真值范围。
补码规格化要求尾数的符号位和第一数位不同,于是其正数最小值为 2 − 1 2^{-1} 2−1,负数最大值为 − ( 2 − 1 + 2 − 9 ) -(2^{-1}+2^{-9}) −(2−1+2−9)!
采用 补码规格化:正数 2 − 1 × 2 − 32 ∼ ( 1 − 2 − 9 ) × 2 31 2^{-1}\times2^{-32}\;\sim\;(1-2^{-9})\times 2^{31} 2−1×2−32∼(1−2−9)×231;负数 − 1 × 2 31 ∼ − ( 2 − 1 + 2 − 9 ) × 2 − 32 -1\times 2^{31}\;\sim\;-(2^{-1}+2^{-9})\times2^{-32} −1×231∼−(2−1+2−9)×2−32。
若 补码非规格化:正数 2 − 9 × 2 − 32 ∼ ( 1 − 2 − 9 ) × 2 31 2^{-9}\times2^{-32}\;\sim\;(1-2^{-9})\times 2^{31} 2−9×2−32∼(1−2−9)×231;负数 − 1 × 2 31 ∼ − 2 − 9 × 2 − 32 -1\times 2^{31}\;\sim\;-2^{-9}\times2^{-32} −1×231∼−2−9×2−32。
6.2.3 ΔIEEE 754标准
IEEE 754中规定了浮点数的格式,如上图。因为规定基值 r = 2 r=2 r=2,所以尾数规格化后,尾数的第一位 S 1 S_1 S1 为定值——原码是1、补码则和符号位相反。于是便可以将这一位省略,称为“隐藏位”,进一步扩大了浮点数的表示范围。下面给出了 IEEE 754 的长度规定:
| 三种浮点数 | 符号位 | 阶码 | 尾数 | 总位数 |
|---|---|---|---|---|
| 短实数 (C语言float) | 1 | 8 | 23 | 32 |
| 长实数 (C语言double) | 1 | 11 | 52 | 64 |
| 临时实数 | 1 | 15 | 64 | 80 |
以上表中“短实数”为例,计算“原码”的取值范围:
- 未规格化:。???
- 规格化(短实数):正数 2 − 1 × 2 − 127 ∼ ( 1 − 2 − 24 ) × 2 127 2^{-1}\times2^{-127}\sim (1-2^{-24})\times2^{127} 2−1×2−127∼(1−2−24)×2127、负数 − ( 1 − 2 − 24 ) × 2 127 ∼ − 2 − 1 × 2 − 127 -(1-2^{-24})\times2^{127}\sim -2^{-1}\times2^{-127} −(1−2−24)×2127∼−2−1×2−127。
可以看到,规格化可以使尾数最高位被省略,于是提升了“浮点数”的精度。
参考视频:“王道-计算机组成原理-2.3.2 IEEE 754”???等待完善内容
??????????????????????????
临时实数没有隐藏位
移码的表示
??????????????????????????
6.3 定点运算
6.3.1 移位运算
1、移位的运算规则
从数学意义上说,“移位”是改变小数点的位置。但是在机器用语中,“移位”则是小数点不动,移动数值部分。若使用二进制存储,移位就表示按2的倍数进行扩大、缩小。“移位”与“加减”配合,能够实现乘除运算。移位分为“算术移位”和“逻辑移位”,下面是给出移位规则:
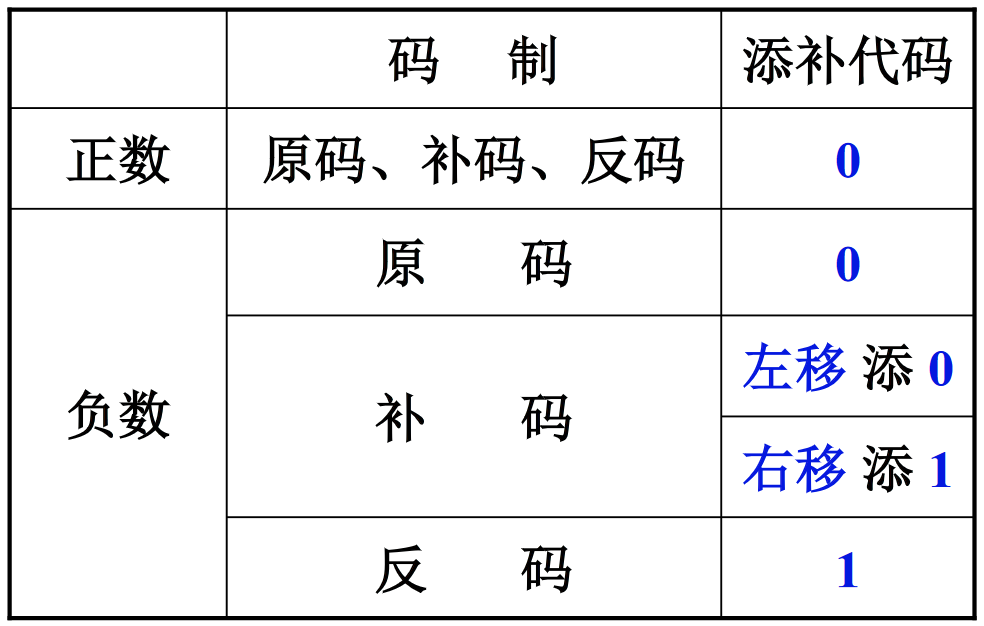

- 算术移位:有符号数的移位。
- 逻辑移位:无符号数的移位。
上述“补码”的移位规则,本质上是建立在原码的移位规则上,负数“左移填0”是因为“原码”最后的“10000”在“补码”中不会改变;负数“右移填1”是因为补码的高位都是“原码”取反。下面是一些练习:
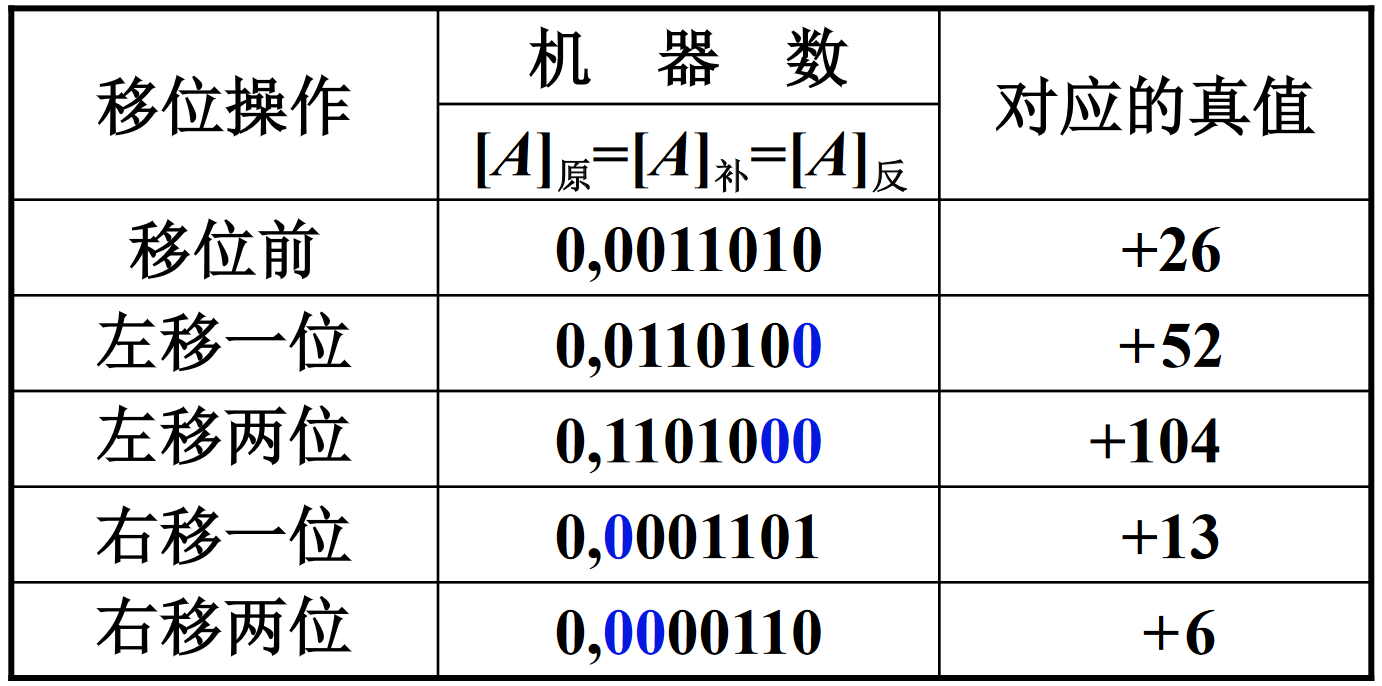
【例6.16】设机器数字长为8位(含1位符号位),写出 A = + 26 A=+26 A=+26 时,三种机器数左、右移一位和两位后的表示形式及对应的真值,并分析结果的正确性。
解: A = − 11010 A=-11010 A=−11010,得 [ A ] 原 = [ A ] 补 = [ A ] 反 = 0 , 001 1010 [A]_{原}=[A]_{补}=[A]_{反}=0,001\;1010 [A]原=[A]补=[A]反=0,0011010,于是【例6.17】设机器数字长为8位(含1位符号位),写出 A = − 26 A=-26 A=−26 时,三种机器数左、右移一位和两位后的表示形式及对应的真值,并分析结果的正确性。
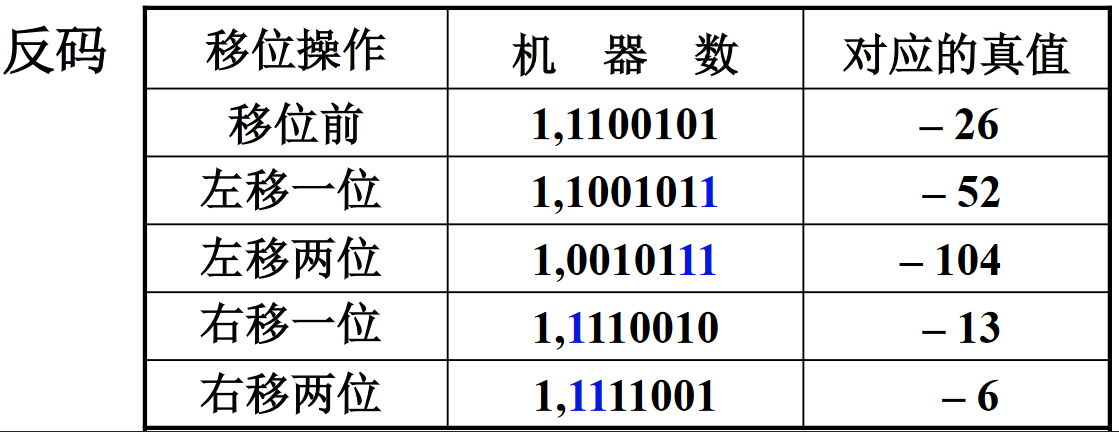
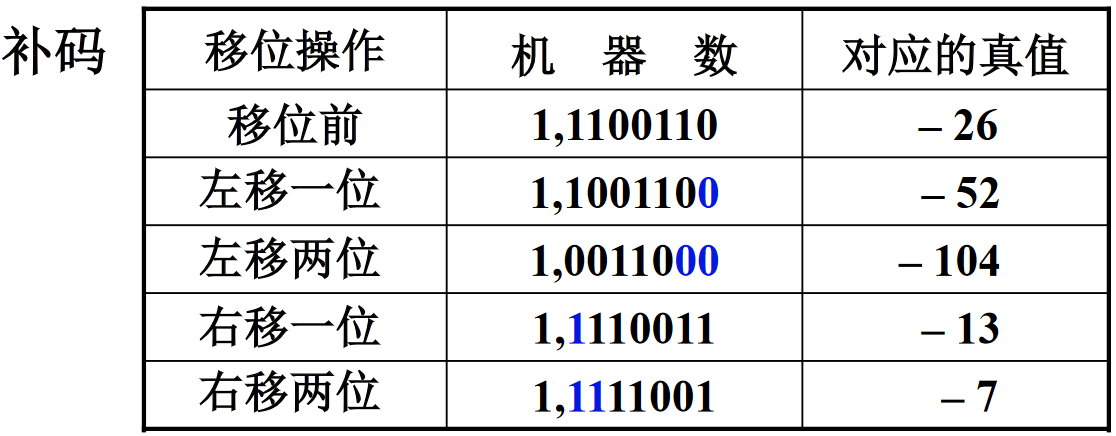
解: A = − 11010 A=-11010 A=−11010,得 [ A ] 原 = 1 , 001 1010 [A]_{原}=1,001\;1010 [A]原=1,0011010、 [ A ] 反 = 1 , 110 0101 [A]_{反}=1,110\;0101 [A]反=1,1100101、 [ A ] 补 = 1 , 110 0110 [A]_{补}=1,110\;0110 [A]补=1,1100110,于是
注:上述两题可以看出,只要没有溢出,计算就非常准确。
2. 移位的硬件实现
当移位移出了1时,就会发生“溢出”。高位溢出称为“出错”,是因为移位后会和正确结果差距很大。低位溢出称为“影响精度”,这是因为移位后和正确结果的偏差不会超过最小精度。和上述移位规则相对应,下面给出了移位的硬件实现。可以看到,如果移位的添补代码是0,那就直接传入;若填补代码是1,还可以利用符号位。如下图:
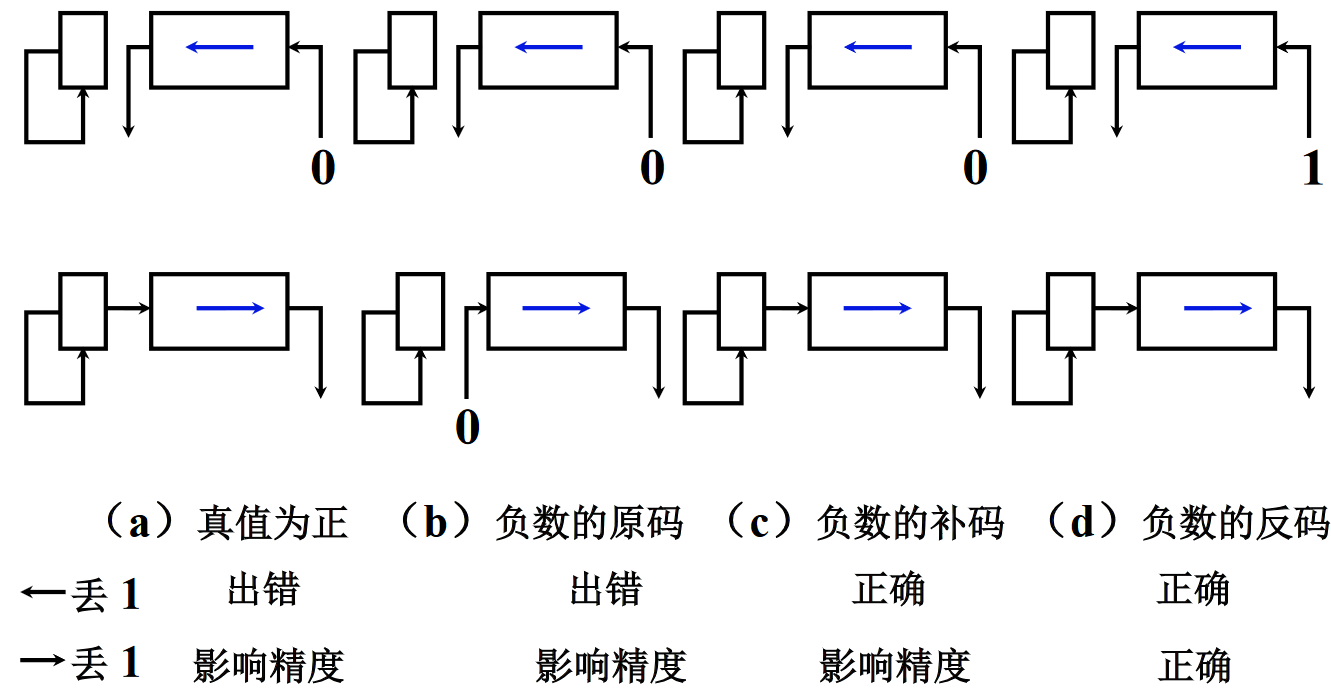
- 左侧方框:符号位所在寄存器。
- 蓝色箭头所在方框:数值部分所在寄存器。
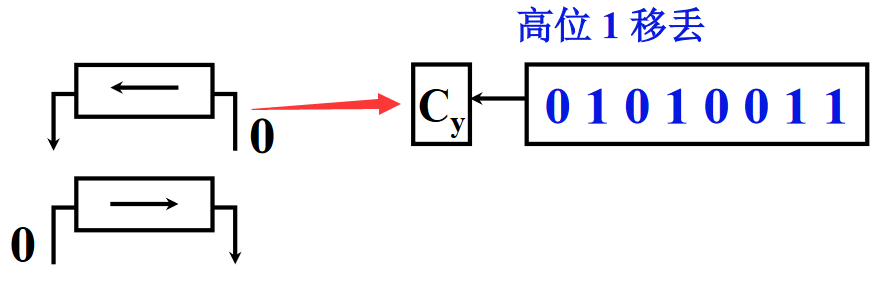
注:为了避免“逻辑左移”将最高位移丢,上右图使用了“带进位的移位”。
6.3.2 加减法运算-补码
1. 补码加减法运算的公式
进行加法运算时,若采用“原码”,那么正数和负数的加法实际上还是减法,而“补码”就是与负数等价的正数。如下给出计算公式,注意相加时连同符号位一起相加,最后舍弃最高的进位即可:

注:【例6.12】中提到过“将 [ y ] 补 [y]_{补} [y]补 连同符号位在内,每位取反,末位加1,即为 [ − y ] 补 [-y]_{补} [−y]补”。
下面给出几个例子:
【例6.18】设 A = 0.1011 A=0.1011 A=0.1011, B = − 0.0101 B=-0.0101 B=−0.0101,求 [ A + B ] 补 [A+B]_{补} [A+B]补?
解: [ A ] 补 + [ B ] 补 = 0.1011 + 1.1011 = 10.0110 [A]_{补}+[B]_{补}=0.1011+1.1011=10.0110 [A]补+[B]补=0.1011+1.1011=10.0110,于是舍弃符号位进位即得 [ A + B ] 补 = 0.0110 [A+B]_{补}=0.0110 [A+B]补=0.0110。【例6.19】设 A = − 9 A=-9 A=−9, B = − 5 B=-5 B=−5,求 [ A + B ] 补 [A+B]_{补} [A+B]补?(假设数值部分是4位)
解: [ A ] 补 + [ B ] 补 = [ 1 , 1001 ] 补 + [ 1 , 0101 ] 补 = 1 , 0111 + 1 , 1011 = 11 , 0010 [A]_{补}+[B]_{补}=[1,1001]_{补}+[1,0101]_{补}=1,0111+1,1011=11,0010 [A]补+[B]补=[1,1001]补+[1,0101]补=1,0111+1,1011=11,0010,于是舍弃符号位进位即得 [ A + B ] 补 = 1 , 0010 [A+B]_{补}=1,0010 [A+B]补=1,0010。【例6.20】设机器数字长为8位(含1位符号位),且 A = 15 A=15 A=15, B = 24 B=24 B=24,用补码求 A − B A-B A−B?
解: [ A ] 补 + [ − B ] 补 = 0 , 000 1111 + [ 1 , 001 1000 ] 补 = 0 , 000 1111 + 1 , 110 1000 = 1 , 111 0111 = [ A − B ] 补 [A]_{补}+[-B]_{补}=0,000\;1111+[1,001\;1000]_{补}=0,000\;1111+1,110\;1000=1,111\;0111=[A-B]_{补} [A]补+[−B]补=0,0001111+[1,0011000]补=0,0001111+1,1101000=1,1110111=[A−B]补,于是 A − B = 1 , 000 1001 = [ − 9 ] 十进制 A-B=1,000\;1001=[-9]_{十进制} A−B=1,0001001=[−9]十进制。【练习1】设机器数字长为5位(含1位符号位),且 x = 9 16 x=\frac{9}{16} x=169, y = 11 16 y=\frac{11}{16} y=1611,用补码求 x + y x+y x+y?
解: [ A ] 补 + [ B ] 补 = 0.1001 + 0.1011 = 1.0100 [A]_{补}+[B]_{补}=0.1001+0.1011=1.0100 [A]补+[B]补=0.1001+0.1011=1.0100,于是得 x + y = 1.1100 = [ − 0.75 ] 十进制 x+y=1.1100=[-0.75]_{十进制} x+y=1.1100=[−0.75]十进制。计算错误!【练习2】设机器数字长为8位(含1位符号位),且 A = − 97 A=-97 A=−97, B = + 41 B=+41 B=+41,用补码求 A − B A-B A−B?
解: [ A ] 补 + [ − B ] 补 = [ 1 , 110 0001 ] 补 + [ 1 , 010 1001 ] 补 = 1 , 001 1111 + 1 , 101 0111 = 10 , 111 0110 [A]_{补}+[-B]_{补}=[1,110\;0001]_{补}+[1,010\;1001]_{补}=1,001\;1111+1,101\;0111=10,111\;0110 [A]补+[−B]补=[1,1100001]补+[1,0101001]补=1,0011111+1,1010111=10,1110110,于是舍弃符号位进位即得 [ A + B ] 补 = 0 , 111 0110 [A+B]_{补}=0,111\;0110 [A+B]补=0,1110110,也就是 A − B = + 118 A-B=+118 A−B=+118。计算错误!注:实际中数值部分字长不是无限的,一定要注意机器数字长,机器数字长不够会导致溢出。
2. 溢出的判断
上面提到补码相加时,需要连通管符号位一起相加,最后舍弃最高的进位。那么如何判断补码溢出呢?如下:
- 使用一位符号位判判断:两个操作数一正一负必不可能溢出;但若两个操作数符号相同,其结果的符号与原操作数的符号不同,即为溢出。缺点是需要记录两个进位,然后进行异或。
- 硬件实现(异或):最高有效位的进位 ⊕ \oplus ⊕ 符号位的进位 = 1,溢出。
- 关键点:“最高有效位的进位”会影响“符号位的进位”。
- 使用两位符号位判溢出:使用两个符号位,新增符号位与原符号位相同。进行加/减运算后,若结果的双符号位相同,未溢出;若结果的双符号位不同,溢出。最高符号位代表其真正的符号。
- 进位判断法:在进行补码加减运算时,可以记录下进位和借位的情况。如果最高位的进位和次高位的进位不同,则表示发生了溢出。
3. 补码加减法的硬件配置
根据上述原理很容易实现补码加减法的硬件配置,如下图:
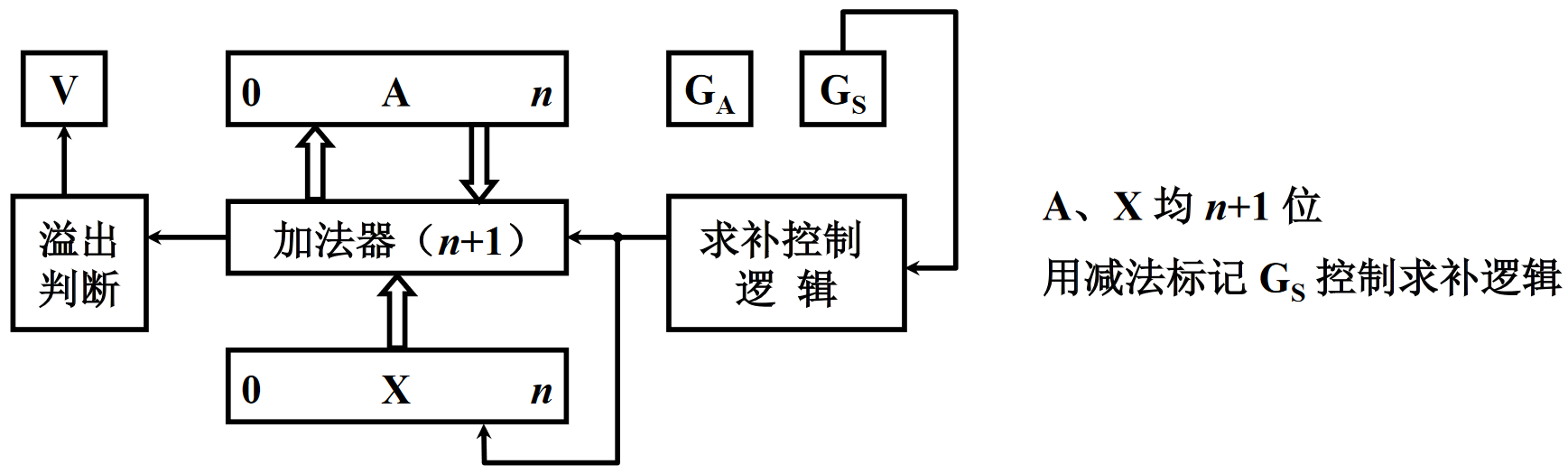
- 加法器:核心部件,完成补码的加减法运算。
- A \text{A} A:也就是 ACC \text{ACC} ACC,保存被加数。
- X \text{X} X:保存加数。
- G A \text{G}_{\text{A}} GA、 G S \text{G}_{\text{S}} GS:加减法标记位。 G A = 1 \text{G}_{\text{A}}=1 GA=1 表示做加法, G S = 1 \text{G}_{\text{S}}=1 GS=1做减法。
- 求补控制逻辑:减法时,控制 X \text{X} X 求解所保存加数的补码,也就是“取反、+1”。
6.3.3 Δ乘法运算-原码
1. 笔算乘法的分析和改进
乘法运算可用“加”和“移位”实现。如下左图,给出了手写的二进制乘法计算过程,可以看到其本质上就是不断的“移位+相加”。但向左移动乘数不符合硬件的逻辑,于是进行改进。最重要的改进就是将遍历过程改为,由乘数的末位决定被乘数是否与原部分积相加,然后右移1位形成新的部分积,同时乘数右移1位(末位移丢),空出高位存放部分积的低位。可以看到乘法计算的中间结果不断占用乘数的空间,如下右图所示:

| 笔算乘法 | 改进 → → → | 硬件改进 |
| 符号位单独处理 | 异或电路 | |
| 乘数的某一位决定是否加被乘数 | 将乘数放到移位寄存器当中 | |
| 4个位积一起相加 | 多次累加 | |
| 乘积的位数扩大一倍 | 两个寄存器 |
重要的改进内容:
- 不断的右移、求和。被乘数只与部分积的高位相加。
- 在保留乘法的中间值的同时,顺便蹭一下乘数的空间。
- 符号位单独使用异或电路计算。
2. 原码乘法—一位乘
上述改进的笔算乘法就是“原码一位乘算法”。原码乘法的特点:
- 乘积的符号位单独处理,数值部分为绝对值相乘。
- 用移位的次数判断乘法是否结束。因为有可能不做加法。
注:移位操作均为“逻辑移位”。
【例6.21】已知 x = − 0.1110 x=-0.1110 x=−0.1110、 y = 0.1101 y=0.1101 y=0.1101,求 [ x ⋅ y ] 原 [x\cdot y]_{原} [x⋅y]原?
解:写出原码后,符号位直接异或,数值部分如右。
3. 原码乘法的硬件配置—一位乘
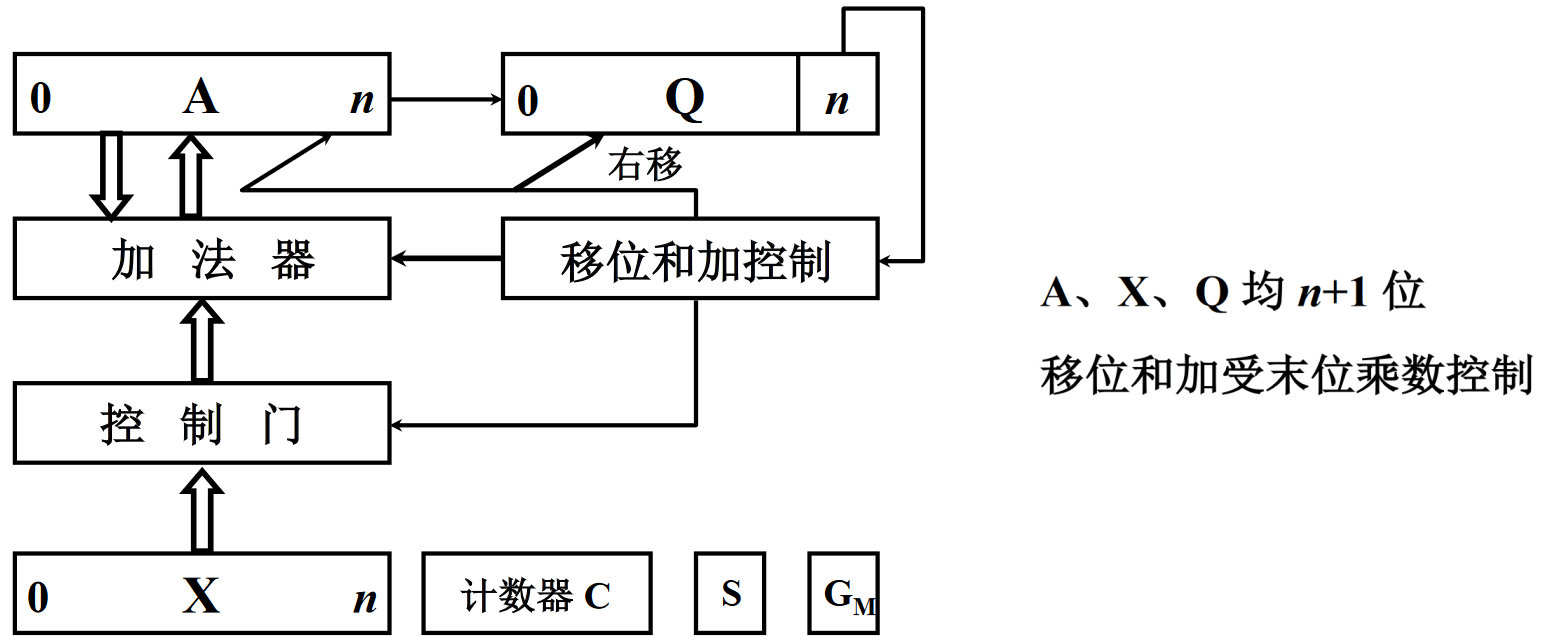
- A \text{A} A:n+1寄存器,也就是 ACC \text{ACC} ACC,保存累加和高位(不断移位)。最高位不是符号位,而是保存低位部分相加后的进位。
- Q \text{Q} Q:n+1寄存器,乘商寄存器。计算刚开始时保存乘数,计算过程不断右移,计算结束后就是乘积的低位。
- X \text{X} X:n+1寄存器,保存被乘数(无需移位)。
- 加法器:n+1位加法器。
- 移位和加控制:由乘数的最低位控制。“控制门”可以送0给加法器。
- 计数器 C \text{C} C:记录移位的次数,判断乘法是否结束。一般是从n递减。
- S \text{S} S:符号位,将两个操作数的符号位异或得到。
- G M \text{G}_\text{M} GM:乘法的标志位。
核心部件:三个n+1位寄存器 A \text{A} A、 Q \text{Q} Q、$\text{X}、一个n+1位全加器。
3. 原码乘法—两位乘
待补充。。。。。。。。
6.3.4 Δ乘法运算-补码
1. 补码乘法—一位乘
(1)补码一位乘运算规则
以小数为例
1.被乘数任意,乘数为正。
与原码乘相似,但加和移位按补码规则运算。乘积的符号自然形成
②被乘数任意,乘数为负
乘数[y]补,去掉符号位,操作同①
最后加[-x]补,校正
2. 补码乘法的硬件配置—一位乘
3. 补码乘法—两位乘
4.乘法小结
- 整数乘法与小数乘法过程完全相同,可用逗号代替小数点。
- 原码乘符号位单独处理;补码乘符号位自然形成。
- 原码乘去掉符号位运算,即为无符号数乘法。
- 不同的乘法运算需有不同的硬件支持。
本小节参考视频:“王道-计算机组成原理-2.2.6.2 补码的乘法运算”???等待完善内容
??????????????????????????
6.3.5 除法运算-原码
约定:
- “小数定点机”除法中,被除数小于除数,这样的到的商还是小数。否则溢出。
- “整数定点机”除法中,被除数大于除数,这样的到的商就是整数。否则溢出。
- 被除数不为0、除数不为0,可以提前通过判断电路规避。
注:上述前两种“溢出”的情况可以见下一节“6.4节-浮点四则运算”。
1. 笔算除法的改进
二进制除法实际上比十进制除法简单,因为二进制商的每一位只有0/1。如下左图所示,给出了笔算除法的过程。我们已经约定好“被除数小于除数”,于是笔算乘法本质上也是不断地比较被除数和当前余数的大小。商的符号位单独处理、数值部分为绝对值相除。按照硬件逻辑进行改进后,和“原码乘法”相反,“原码除法”是从低位计算到高位。如下:

| 笔算除法 | 改进 → → → | 硬件改进 |
| 商符单独处理 | 符号位异或电路 | |
| 心算上商 |x|-|y|>0上商1、|x|-|y|<0上商0 | 加法电路给出上商 | |
| 余数不动低位补“0”,减右移一位的除数 | 余数左移一位低位补“0”,减除数 | |
| 2倍字长加法器 | 1倍字长加法器 | |
| 上商位置不固定 | 在寄存器最末位上商,然后左移 |
重要的改进内容:
- 不断的左移、求和。每次都与“负的除数绝对值的补码”低位相加。
- 不断缩小余数的中间值的空间,最终只剩下商。
- 符号位单独使用异或电路计算。
2. 原码除法:恢复余数法
在第 i i i 步:
- 上商:若余数 R i > 0 R_i>0 Ri>0,上商1;若余数 R i < 0 R_i<0 Ri<0,上商0。
- 恢复余数:若上商1,则跳转到下一步;若上商0,恢复余数 R i + y ∗ R_i+y^* Ri+y∗。
- 逻辑移位:将余数逻辑左移1位。
- 准备下一次运算:再将现在的余数减去 y ∗ y^* y∗,得到下一次余数 R i + 1 R_{i+1} Ri+1。
特点:若数值部分为n位,则上商n+1次,其中第一次上商判溢出。移位n次。加n+1~2n+1次。用移位的次数判断除法是否结束。
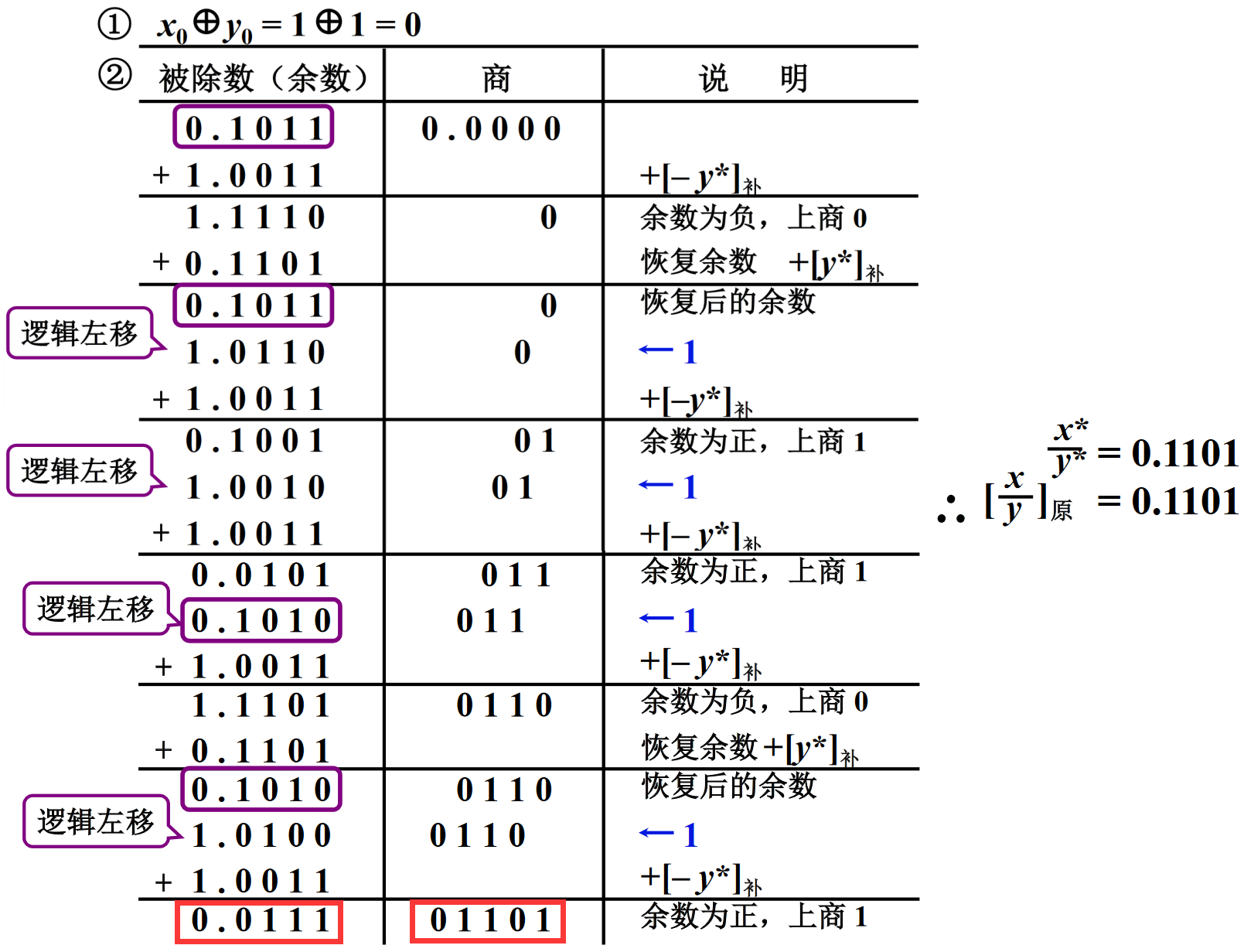
【例6.24】假设机器字长5位(符号位1位),给出 x = − 0.1011 x=-0.1011 x=−0.1011、 y = − 0.1101 y=-0.1101 y=−0.1101,在小数定点机中求 [ x y ] 原 [\frac{x}{y}]_{原} [yx]原?
解: [ x ] 原 = 1.1011 [x]_{原}=1.1011 [x]原=1.1011、 [ y ] 原 = 1.1101 [y]_{原}=1.1101 [y]原=1.1101, [ y ∗ ] 补 = 0.1101 [y^*]_{补}= 0.1101 [y∗]补=0.1101、 [ − y ∗ ] 补 = 1.0011 [-y^*]_{补}= 1.0011 [−y∗]补=1.0011。然后如下:
- 每一步:首先判断上商、若上商0则进行“加法”恢复余数、然后余数“逻辑左移”、最后进行“加法”用于下一次判断。
- 上图中未展示“第一次上商”,其作用是判断是否溢出。不符合本节开始提到的“约定”。
3. 原码除法:加减交替法
“加减交替法”是对“恢复余数法”的改进,将每一步中的两次加法合并,直接节省掉“恢复余数法”中“恢复余数”的过程。如下:
在第 i i i 步:
- 若为第一步直接 + y ∗ +y^* +y∗。
- 否则,若余数 R i > 0 R_i>0 Ri>0,则上商1,计算新的余数 R i + 1 = 2 R i − y ∗ R_{i+1}=2R_i-y^* Ri+1=2Ri−y∗。
- 否则,若余数 R i < 0 R_i<0 Ri<0,则上商0,计算新的余数 R i + 1 = 2 ( R i + y ∗ ) − y ∗ = 2 R i + y ∗ R_{i+1}=2(R_i+y^*)-y^*=2R_i+y^* Ri+1=2(Ri+y∗)−y∗=2Ri+y∗。
- 如果最后一步且上商为0,则最后加法计算的结果不是对应的余数,还需要再 + y ∗ +y^* +y∗ 恢复余数。
特点:若数值部分为n位,则上商n+1次,第一次上商判溢出。移位n次。加(n+1)/(n+2)次。用移位的次数判断除法是否结束。
【例6.25】假设机器字长5位(符号位1位),给出 x = − 0.1011 x=-0.1011 x=−0.1011、 y = − 0.1101 y=-0.1101 y=−0.1101,在小数定点机中求 [ x y ] 原 [\frac{x}{y}]_{原} [yx]原?
解: [ x ] 原 = 1.1011 [x]_{原}=1.1011 [x]原=1.1011、 [ y ] 原 = 1.1101 [y]_{原}=1.1101 [y]原=1.1101, [ x ∗ ] 补 = 0.1011 [x^*]_{补}= 0.1011 [x∗]补=0.1011、 [ y ∗ ] 补 = 0.1101 [y^*]_{补}= 0.1101 [y∗]补=0.1101、 [ − y ∗ ] 补 = 1.0011 [-y^*]_{补}= 1.0011 [−y∗]补=1.0011。然后如下:
4. 加减交替法的硬件配置

- A \text{A} A:n+1寄存器,也就是 ACC \text{ACC} ACC。一开始保存被除数,计算过程不断左移,最后就是余数。最高位不是符号位,而是保存高位部分相加后的进位。
- Q \text{Q} Q:n+1寄存器,乘商寄存器。计算刚开始时保存0,计算过程不断右移,计算结束后就是商。
- X \text{X} X:n+1寄存器,保存除数(无需移位)。
- 加法器:n+1位加法器。
- 移位和加控制逻辑:最低位控制加减交替。“控制门”可以送 + y ∗ +y^* +y∗、 − y ∗ -y^* −y∗ 给加法器。
- 计数器 C \text{C} C:记录移位的次数,判断除法是否结束。
- S \text{S} S:符号位,将两个操作数的符号位异或得到。
- G D \text{G}_\text{D} GD:除法的标志位。
- V \text{V} V:表示是否溢出。
6.3.6 Δ除法运算-补码
补码除法也分恢复余数法和加减交替法,后者用得较多,在此只讨论加减交替法。
参考视频:“王道-计算机组成原理-2.2.7.2 补码的除法运算”???等待完善内容
??????????????????????????
6.4 浮点四则运算
6.4.1 浮点数的加减运算
1. 浮点数加减运算的基本步骤
假设浮点数基数为2,并且使用“补码”计算,下面直接直接给出“浮点加减运算”的基本步骤:
- 对阶:首先用补码求阶差 [ Δ j ] 补 = [ j x ] 补 − [ j y ] 补 [\Delta_j]_{补}=[j_x]_{补}-[j_y]_{补} [Δj]补=[jx]补−[jy]补,然后“小阶向大阶看齐”。小阶所在的浮点数阶码增加、尾数算数右移。注意“右移”只是可能影响数据精度,而“左移”可能会出现特别大的错误。
- 尾数求和:补码定点求和,注意要重复一位符号位。
- 尾数规格化:非规格化时,检查尾数的两个符号位,若为 10 / 01 10/01 10/01 则“右规”;否则就“左规”。每次移位都是算术移位,同时需要调整阶码。尾数溢出则“右规”。
- 原码规格化原则是第一数位为1。
- 补码规格化原则是符号位和第一数位不同。
注:若计算结果溢出(参考“6.2.2 浮点表示”),下溢全部按照机器零处理。上溢会进入“出错处理”。
2. 舍入方法和溢出判断
需要注意的是,上述“对阶”和“规格化”过程中,只要进行尾数右移时,丢失有效数字就会引起误差,于是便有下面的舍入方法:
- 截断法:直接移出。后续没有任何操作。上述“计算步骤”中的默认方法。
- 0舍1入法:移出的是1,移动后,就在最末尾加1。可能会使尾数再次溢出。类似于“四舍五入”。
- 恒置“1”法:只要右移,就强制使末位为1。
- …
计算完成之后再判断是否溢出。“溢出判断”较为简单,只要计算结果超出范围就是溢出。“上溢”需要进入“出错处理”,“下溢”则按照“机器零”处理:
- 阶码判断法:阶码为0,判断为下溢,按照“机器零”处理。若阶码采用补码,且为补码的最小负数(符号位为1、其余位都是0),判定为上溢,进入“出错处理”。
- 尾数判断法:尾数为0,就判定为下溢,按照“机器零”处理。
最后给出两个例题,理解浮点数的加减运算过程:
【例6.27】 x = 0.1101 × 2 10 x= 0.1101\times 2^{10} x=0.1101×210、 y = 0.1011 × 2 01 y= 0.1011\times 2^{01} y=0.1011×201,求 x + y x+y x+y?(除阶符、数符外,阶码取3位,尾数取6位)
解: [ x ] 补 = 00 , 010 ; 00.110100 [x]_{补}=00,010;\;00.110100 [x]补=00,010;00.110100, [ y ] 补 = 00 , 001 ; 00.101100 [y]_{补}=00,001;\;00.101100 [y]补=00,001;00.101100。
- 对阶:阶差为1,则 y y y 阶码+1、尾数算数右移1位, [ y ] 补 ′ = 00 , 010 ; 00.010110 [y]_{补'}=00,010;\;00.010110 [y]补′=00,010;00.010110。(没有误差)
- 尾数求和: [ S x ] 补 + [ S y ] 补 ′ = 00.110100 + 00.010110 = 01.001010 [S_x]_{补}+[S_y]_{补'}=00.110100+00.010110=01.001010 [Sx]补+[Sy]补′=00.110100+00.010110=01.001010。
- 尾数规格化:补码规格化,尾数溢出则“右规”1位、阶码+1,得结果 [ x + y ] 补 = 00 , 011 ; 00.100101 [x+y]_{补}=00,011;\;00.100101 [x+y]补=00,011;00.100101,于是 x + y = 00 , 011 00.100101 = + 37 64 × 2 3 x+y=00,011\;00.100101=+\frac{37}{64}\times 2^{3} x+y=00,01100.100101=+6437×23。(准确结果)
【例6.28】 x = − 5 8 × 2 − 5 x= -\frac{5}{8}\times 2^{-5} x=−85×2−5、 y = 7 8 × 2 − 4 y= \frac{7}{8}\times 2^{-4} y=87×2−4,求 x − y x-y x−y?(除阶符、数符外,阶码取3位,尾数取6位)
解: [ x ] 补 = [ 1 , 101 ; 1.101000 ] 补 = 11 , 011 ; 11.011000 [x]_{补}=[1,101;\;1.101000]_{补}=11,011;\;11.011000 [x]补=[1,101;1.101000]补=11,011;11.011000, [ y ] 补 = [ 1 , 100 ; 0.111000 ] 补 = 11 , 100 ; 00.111000 [y]_{补}=[1,100;\;0.111000]_{补}=11,100;\;00.111000 [y]补=[1,100;0.111000]补=11,100;00.111000。
- 对阶:阶差为-1,则 x x x 阶码+1、尾数算数右移1位, [ x ] 补 ′ = 11 , 100 ; 11.101100 [x]_{补'}=11,100;\;11.101100 [x]补′=11,100;11.101100。(没有误差)
- 尾数求和: [ S x ] 补 ′ + [ − S y ] 补 = 11.101100 + 11.001000 = 110.110100 [S_x]_{补'}+[-S_y]_{补}=11.101100+11.001000=110.110100 [Sx]补′+[−Sy]补=11.101100+11.001000=110.110100,舍弃符号位进位得 10.110100 10.110100 10.110100。
- 尾数规格化:补码规格化,尾数溢出则“右规”1位、阶码+1,得结果 [ x − y ] 补 = 11 , 101 ; 11.011010 [x-y]_{补}=11,101;\;11.011010 [x−y]补=11,101;11.011010,于是 x − y = 11 , 011 ; 11.100110 = − 19 32 × 2 − 3 x-y=11,011;\;11.100110=-\frac{19}{32}\times 2^{-3} x−y=11,011;11.100110=−3219×2−3。(准确结果)
6.4.2 Δ浮点数的乘除运算
待补充。。。。。
符号阶码和尾数分开按类似于定点的运算然后合并,感觉浮点数乘除要比加减简单。
6.4.3 Δ浮点运算的硬件配置
待补充。。。。。。。
浮点运算器主要由两个定点运算部件组成,一个是阶码运算部件,另一个是尾数运算部件。
6.5 算术逻辑单元
6.5.1 ALU电路
前面已经介绍了定点运算、浮点运算、算术运算、逻辑运算的硬件电路,实际上这些运算都被集成到一个集成电路芯片中,也就是ALU(Arithmetic and Logic Unit,算逻运算单元)。ALU是组合逻辑电路,若需要保存结果,还需要额外添加寄存器。ALU再和“控制器”集成在一起,就构成了计算机系统的CPU。如下左图是ALU电路的表示符号,其中 k i k_i ki 控制ALU进行“算术运算”还是“逻辑运算”:
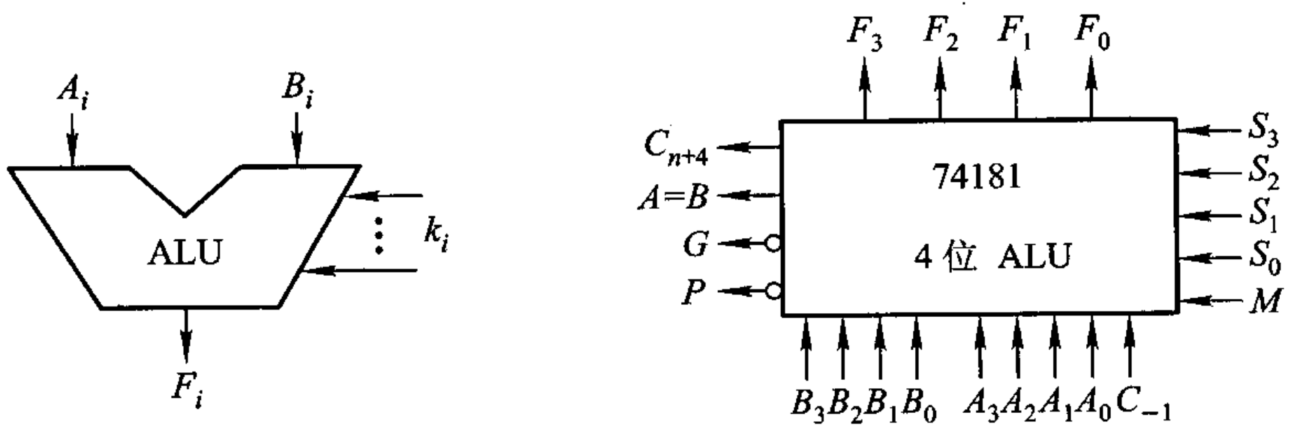
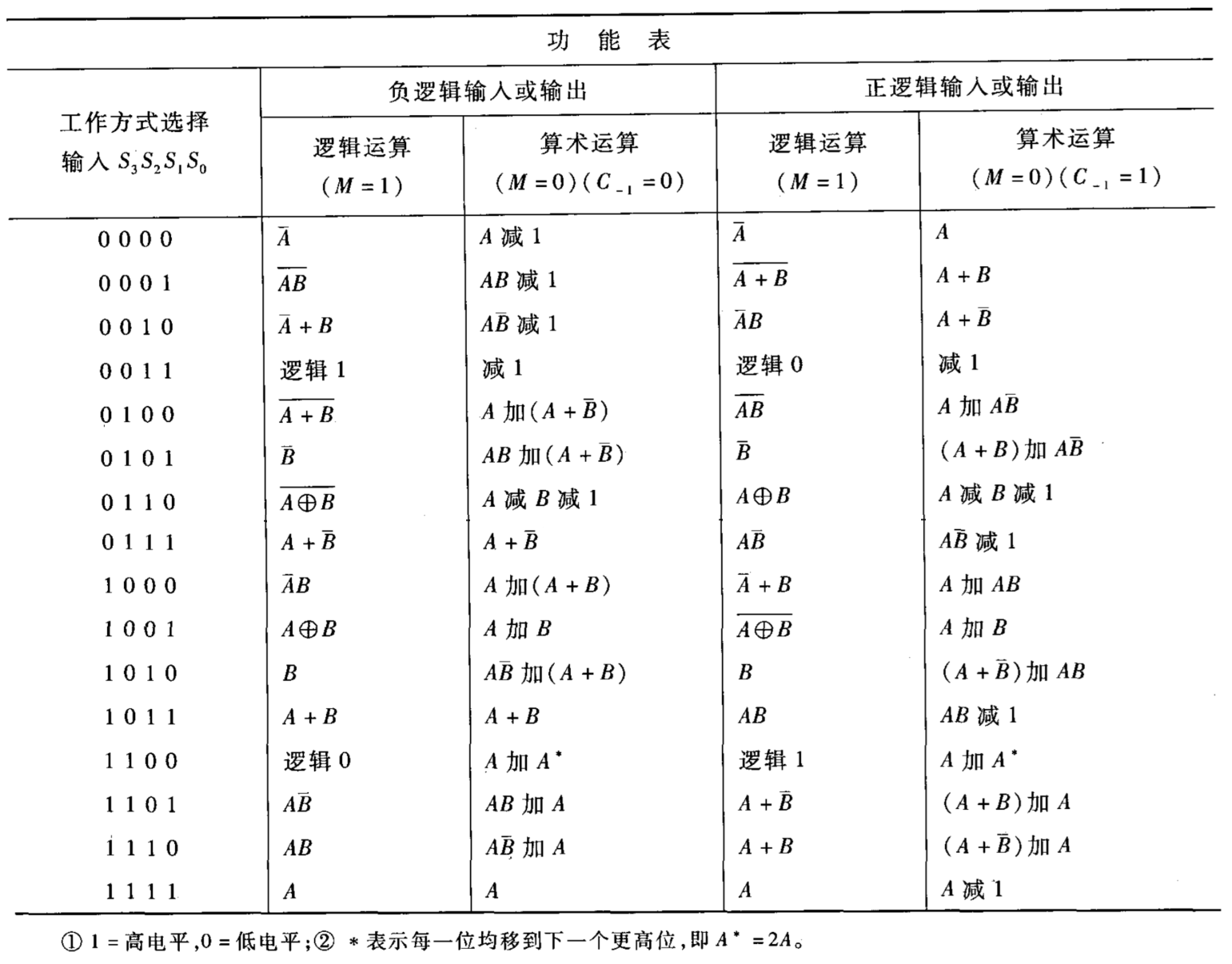
但ALU只能实现“1位”的算逻运算,要完成“多位”的算逻运算还要将几个ALU集成在一起,如上右图74181中就集成了4个ALU,可以完成4位的算逻运算。下面给出74181的功能表:
6.5.2 快速进位链
那上述74181内部是如何连接多个ALU的呢?本节以“加法器”为例,介绍算术运算、逻辑运算的电路优化问题。根据“数字电子技术基础”的执行,要实现n位加法运算,可以使用n+1个“全加器”构成的一个“并行加法器”。之所以称之为“并行”,是因为两个n+1的数,可以利用该加法器以并行的方式完成加法运算。如下图所示,每个 FA i \text{FA}_i FAi 都是一个全加器:
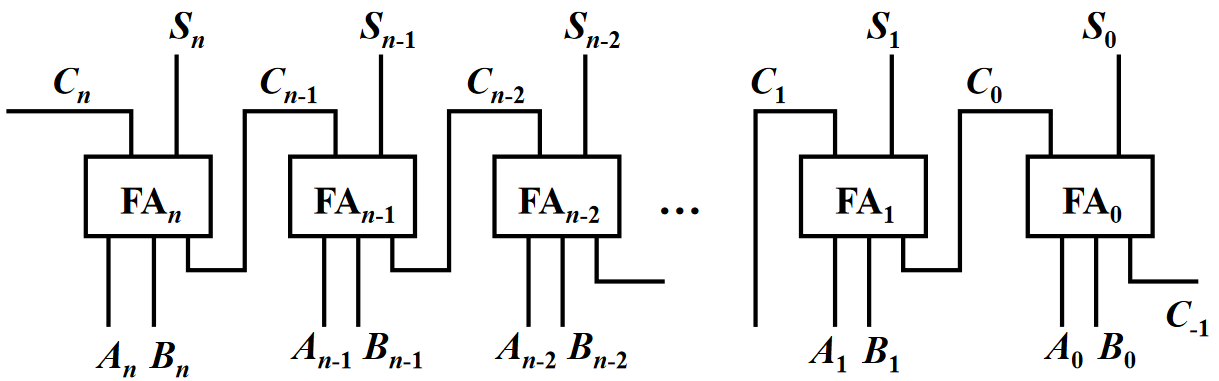
- 和的计算: S i = A ‾ i B ‾ i C i − 1 + A ‾ i B i C ‾ i − 1 + A i B ‾ i C ‾ i − 1 + A i B i C i − 1 S_i=\overline{A}_i\overline{B}_iC_{i-1}+\overline{A}_iB_i\overline{C}_{i-1}+A_i\overline{B}_i\overline{C}_{i-1}+A_iB_iC_{i-1} Si=AiBiCi−1+AiBiCi−1+AiBiCi−1+AiBiCi−1
- 进位的计算: C i = A ‾ i B i C i − 1 + A i B ‾ i C i − 1 + A i B i C ‾ i − 1 + A i B i C i − 1 = A i B i + ( A i + B i ) C i − 1 C_i=\overline{A}_iB_iC_{i-1}+A_i\overline{B}_iC_{i-1}+A_iB_i\overline{C}_{i-1}+A_iB_iC_{i-1}=A_iB_i+(A_i+B_i)C_{i-1} Ci=AiBiCi−1+AiBiCi−1+AiBiCi−1+AiBiCi−1=AiBi+(Ai+Bi)Ci−1
但显然,依照上图的连接方式,每个“全加器”都需要等待上一级“进位”输入,才能输出本级的计算结果。每一级全加器的进位前后连接,形成“进位链”。于是,并行加法器的运算瓶颈在于“进位链”。
上图给出进位的链的改进思路及指标,下面来依次介绍。假设级延迟时间“与非门/或门” t y t_y ty、“与或非门” 1.5 t y 1.5t_y 1.5ty。
1. 串行进位链
前面所示的“并行加法器”结构实际上就是采用了“串行进位链”,进位逐级产生。我们可以将进位的计算专门抽出来,给出如下的进位递推公式:
C i = A i B i + ( A i + B i ) C i − 1 = 令 t i = A i + B i 令 d i = A i B i d i + t i C i − 1 = 德 ⋅ 摩根定律 d i ‾ ⋅ t i C i − 1 ‾ ‾ C_i=A_iB_i+(A_i+B_i)C_{i-1}\xlongequal[令t_i=A_i+B_i]{令d_i=A_iB_i}d_i+t_iC_{i-1}\xlongequal{德·摩根定律}\overline{\overline{d_i}\cdot\overline{t_iC_{i-1}}} Ci=AiBi+(Ai+Bi)Ci−1令di=AiBi令ti=Ai+Bidi+tiCi−1德⋅摩根定律di⋅tiCi−1
- 本地进位: d i = A i B i d_i=A_iB_i di=AiBi
- 传递进位: t i = A i + B i t_i=A_i+B_i ti=Ai+Bi
上述两者均与外来进位无关。

假设“与非门”的级延迟时间为 t y t_y ty,当所有的 d i d_i di、 t i t_i ti 形成后,4位全加器需要 8 t y 8t_y 8ty 产生全部进位, n n n 位全加器需要 2 n t y 2nt_y 2nty 产生全部进位。
2. 并行进位链-普通版
“并行进位链”的宗旨就是“同时产生”n位加法器的进位,被称为先行进位/跳跃进位。最直观的想法就是根据进位的递推公式,将所有进位的计算直接暴力展开,于是 所有的进位都可以直接产生:
C 0 = d 0 + t 0 C − 1 C 1 = d 1 + t 1 C 0 = d 1 + t 1 d 0 + t 1 t 0 C − 1 C 2 = d 2 + t 2 C 1 = d 2 + t 2 d 1 + t 2 t 1 d 0 + t 2 t 1 t 0 C − 1 C 3 = d 3 + t 3 C 2 = d 3 + t 3 d 2 + t 3 t 2 d 1 + t 3 t 2 t 1 d 0 + t 3 t 2 t 1 t 0 C − 1 \begin{aligned} & C_0 = d_0+t_0C_{-1}\\ & C_1 = d_1+t_1C_{0} = d_1+t_1d_0+t_1t_0C_{-1}\\ & C_2 = d_2+t_2C_{1} = d_2+t_2d_1+t_2t_1d_0+t_2t_1t_0C_{-1}\\ & C_3 = d_3+t_3C_{2} = d_3+t_3d_2+t_3t_2d_1+t_3t_2t_1d_0+t_3t_2t_1t_0C_{-1}\\ \end{aligned} C0=d0+t0C−1C1=d1+t1C0=d1+t1d0+t1t0C−1C2=d2+t2C1=d2+t2d1+t2t1d0+t2t1t0C−1C3=d3+t3C2=d3+t3d2+t3t2d1+t3t2t1d0+t3t2t1t0C−1

假设级延迟时间“与非门/或门” t y t_y ty、“与或非门” 1.5 t y 1.5t_y 1.5ty,当所有的 d i d_i di、 t i t_i ti 形成后,优点是不管有多少进位,只要“与或非门”能连接足够的输入,n位全加器只需 2.5 t y 2.5t_y 2.5ty 就能产生全部进位(上图中n=4)。缺点是电路连接非常复杂,一般也就做到上述4位。于是便给出下面的折衷方式。
3. 并行进位链-单重分组跳跃进位链
“单重分组跳跃进位链”的思路是将n位全加器分若干小组,小组中的进位同时产生,小组与小组之间采用串行进位。每一个小组内部,都采用上述普通版的并行进位链:
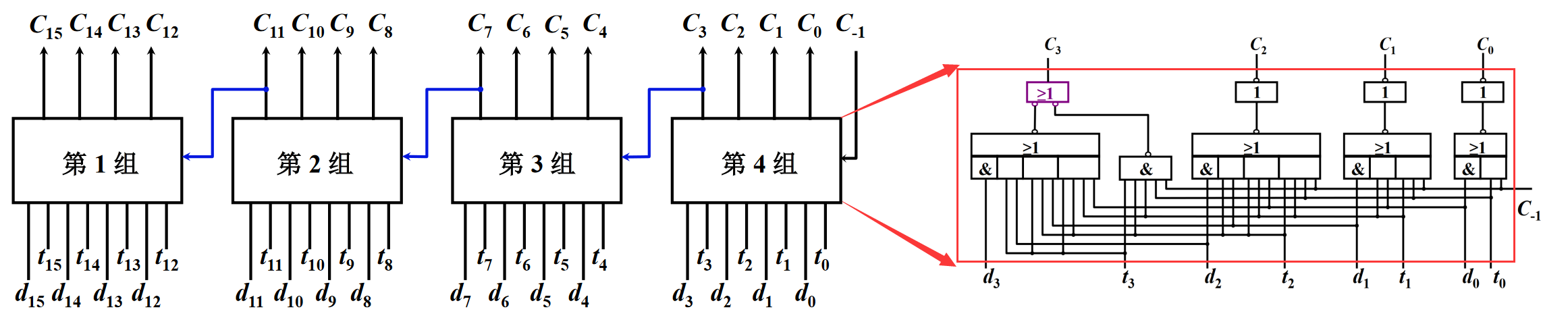
根据前面假设,当所有的 d i d_i di、 t i t_i ti 形成后,4位全加器只需 2.5 t y 2.5t_y 2.5ty 就能产生全部进位,于是上述16位全加器需要 10 t y 10t_y 10ty 就能产生全部进位(串行进位链需要 32 t y 32t_y 32ty)。
4. 并行进位链-双重分组跳跃进位链
“双重分组跳跃进位链”的思路是将n位全加器分若干大组,大组中又包含若干小组。每个大组中,小组的最高位进位同时产生,小组间的进位同时产生,大组与大组之间采用串行进位。对于单个大组来说,第一重进位由各个小组完成,但注意高位的小组(如5、6、7)都需要等待第二重小组计算完毕才能计算进位。每个小组本质上都是前面介绍的普通版“并行进位链”,只不过不计算最高位的进位,而是生成 D i D_i Di、 T i T_i Ti (生成方式如下公式)。小组间的连接方式如下图,假设每个小组都是4位加法器:
C 3 = d 3 + t 3 d 2 + t 3 t 2 d 1 + t 3 t 2 t 1 d 0 + t 3 t 2 t 1 t 0 C − 1 = 令 T 8 = t 3 t 2 t 1 t 0 令 D 8 = d 3 + t 3 d 2 + t 3 t 2 d 1 + t 3 t 2 t 1 d 0 = D 8 + T 8 C − 1 C 7 = D 7 + T 7 C 3 = D 7 + T 7 D 8 + T 7 T 8 C − 1 C 11 = D 6 + T 6 C 7 = D 6 + T 6 D 7 + T 6 T 7 D 8 + T 6 T 7 T 8 C − 1 C 15 = D 5 + T 5 C 11 = D 5 + T 5 D 6 + T 5 T 6 T 7 + T 5 T 6 T 7 D 8 + T 5 T 6 T 7 T 8 C − 1 \begin{aligned} C_3 &= d_3+t_3d_2+t_3t_2d_1+t_3t_2t_1d_0+t_3t_2t_1t_0C_{-1} \xlongequal[令T_8=t_3t_2t_1t_0]{令 D_8=d_3+t_3d_2+t_3t_2d_1+t_3t_2t_1d_0}=D_8+T_8C_{-1}\\ C_7 &= D_7+T_7C_{3} = D_7+T_7D_8+T_7T_8C_{-1}\\ C_{11} &= D_6+T_6C_{7} = D_6+T_6D_7+T_6T_7D_8+T_6T_7T_8C_{-1}\\ C_{15} &= D_5+T_5C_{11} = D_5+T_5D_6+T_5T_6T_7+T_5T_6T_7D_8+T_5T_6T_7T_8C_{-1}\\ \end{aligned} C3C7C11C15=d3+t3d2+t3t2d1+t3t2t1d0+t3t2t1t0C−1令D8=d3+t3d2+t3t2d1+t3t2t1d0令T8=t3t2t1t0=D8+T8C−1=D7+T7C3=D7+T7D8+T7T8C−1=D6+T6C7=D6+T6D7+T6T7D8+T6T7T8C−1=D5+T5C11=D5+T5D6+T5T6T7+T5T6T7D8+T5T6T7T8C−1
- 第 i i i 小组的本地进位: D i = d 3 + t 3 d 2 + t 3 t 2 d 1 + t 3 t 2 t 1 d 0 D_i=d_3+t_3d_2+t_3t_2d_1+t_3t_2t_1d_0 Di=d3+t3d2+t3t2d1+t3t2t1d0
- 第 i i i 小组的传送条件: T i = t 3 t 2 t 1 t 0 T_i=t_3t_2t_1t_0 Ti=t3t2t1t0
上述两者均与外来进位无关,且在本小组内连线固定。
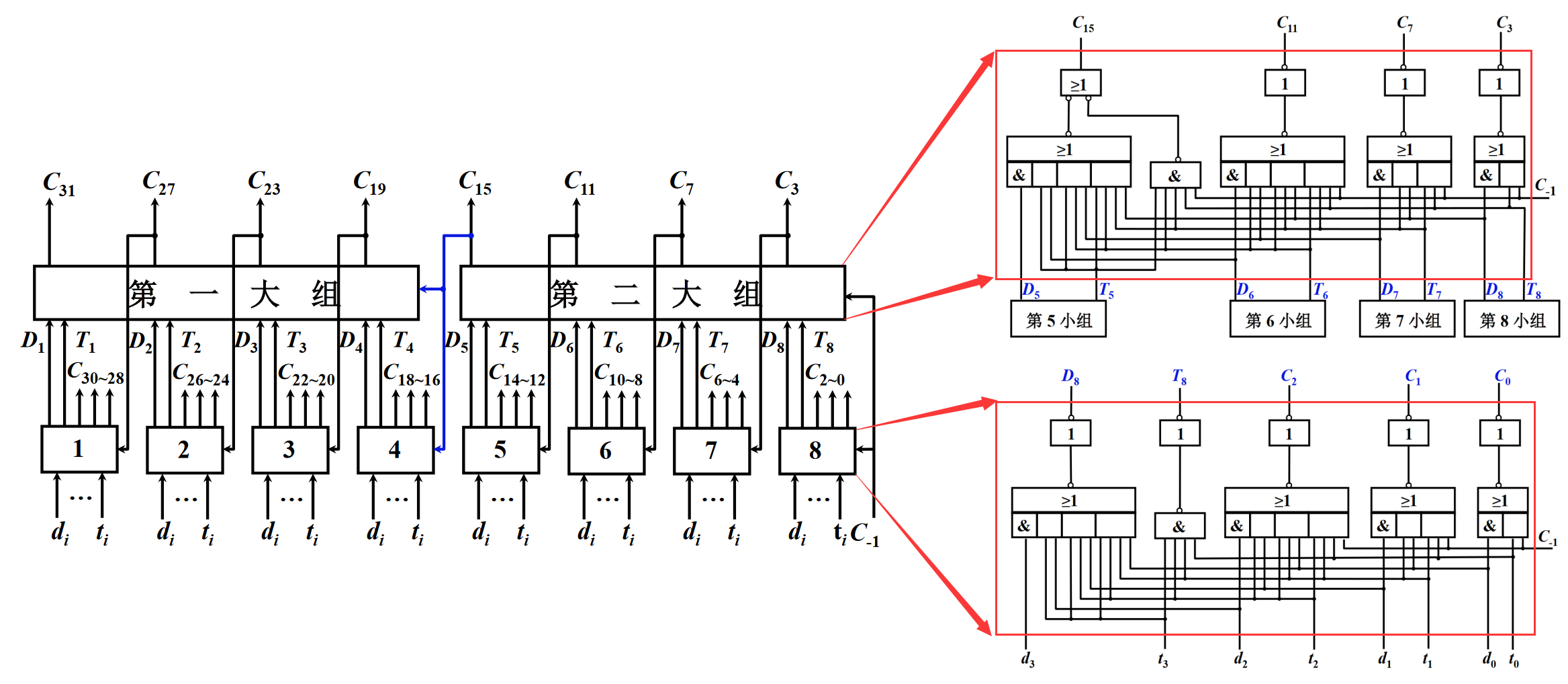
当所有的 d i d_i di、 t i t_i ti、 C − 1 C_{-1} C−1 形成后,有如下的计算步骤:
- 2.5 t y 2.5t_y 2.5ty 时刻:所有小组计算所有的 D i D_i Di、 T i T_i Ti;第8小组额外计算出自己的进位 C 2 C_2 C2、 C 1 C_1 C1、 C 0 C_0 C0。
- 5 t y 5t_y 5ty 时刻:第二大组计算出第二重的四个进位 C 3 C_3 C3、 C 7 C_7 C7、 C 11 C_{11} C11、 C 15 C_{15} C15。
- 7.5 t y 7.5t_y 7.5ty 时刻:第4、5、6、7小组计算出自己的所有进位;第一大组计算出第二重的四个进位 C 19 C_{19} C19、 C 23 C_{23} C23、 C 27 C_{27} C27、 C 31 C_{31} C31。
- 10 t y 10t_y 10ty 时刻:第1、2、3小组计算出自己的所有进位。
总结一下,使用双重分组跳跃进位链,32位全加器只需要 10 t y 10t_y 10ty 就能产生全部进位,而“单重分组的并行进位链”需要 20 t y 20t_y 20ty、“串行进位链”需要 64 t y 64t_y 64ty。